Deltoid

Nożyczki matematyczne

Jedną z najsłynniejszych niemożliwych rzeczy w matematyce jest konstrukcja samym cyrklem i linijką kwadratu o polu równym polu danego koła. Problem ten, zwany kwadraturą koła, rozważano już w starożytnej Grecji, ale rozwiązano go, czyli udowodniono niekonstruowalność, dopiero w XIX wieku.

Twierdzenie (Wallace-Bolyai-Gerwien). Dowolny wielokąt można pociąć nożyczkami na skończenie wiele kawałków, a następnie ułożyć z nich dowolny inny wielokąt o tym samym polu.

Może da się wykonać tego rodzaju "kwadraturę koła"?

Problem. Czy można tak pociąć koło nożyczkami na skończenie wiele części, by następnie ułożyć z nich kwadrat?

Rozwiązanie. Pokażemy, że nie jest to możliwe. Rozetnijmy koło nożyczkami na skończenie wiele części. Można przyjąć, że każdy fragment brzegu każdego z obszarów jest "porządny": wypukły, wklęsły lub prosty i że ma określoną długość. Niech w każdej części tak podzielonego koła mieszka krasnoludek. Każdy z krasnoludków maluje od swojej strony płot otaczający jego teren: na kolorowo fragmenty wypukłe, na szaro - wklęsłe, na czarno - proste (rysunek obok).

Zauważmy, że jeśli fragment płotu jest z jednej strony czarny, to jest czarny również z drugiej strony. Z kolei jeśli krasnoludek pomalował część płotu na szaro, to jego sąsiad pomalował tę część od swojej strony na kolorowo. I na odwrót, za wyjątkiem fragmentów płotu ograniczających całe koło, które są pomalowane tylko z jednej strony, na kolorowo. Stąd łączna długość wszystkich kolorowych części płotu jest większa od łącznej długości szarych części właśnie o obwód koła.

Przypuśćmy, że można z rozważanych kawałków koła ułożyć kwadrat. Jego brzeg jest prosty, więc aby części wewnątrz do siebie pasowały, musiałaby być taka sama łączna długość kolorowych i szarych fragmentów ich brzegów, sprzecznie z powyższą obserwacją. Wobec tego nie da się wykonać takiej "kwadratury koła".

***

W obliczu poniesionej porażki, sięgnijmy po silniejsze narzędzie - "nożyczki matematyczne". Różnią się one od zwykłych tym, że pozwalają dzielić figurę na dowolne podzbiory, również te niemożliwe do wycięcia zwykłymi nożyczkami, jak pojedyncze punkty, odcinki etc. Uwzględniamy przy tych podziałach przynależność wszystkich punktów figury, również tych z ewentualnych linii podziału.

Problem. Czy można tak podzielić koło na skończenie wiele części, by następnie ułożyć z nich kwadrat?

Pytanie to postawił w 1925 roku Alfred Tarski, a odpowiedzi udzielił Miklós Laczkovich w roku 1990. Udowodnił on, że taka "kwadratura koła" jest możliwa przez podział koła na... mniej więcej 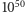$|1050$ części!

***

W starożytnej Grecji rozważano również inny słynny problem - podwojenie sześcianu, czyli konstrukcję sześcianu o objętości dwukrotnie większej od danego sześcianu. Ona również okazała się niemożliwa do wykonania cyrklem i linijką.

Problem. Czy można podzielić sześcian na skończenie wiele części i zbudować z nich sześcian o dwukrotnie większej objętości?

Na podziały zwykłymi nożyczkami (lub nożem) nie ma co liczyć, bowiem zachowują one objętość figur, a my objętość chcemy podwoić. Wydawać by się mogło, że z tego właśnie powodu żądany podział sześcianu w ogóle nie jest możliwy.

Jedna z wersji słynnego paradoksu Banacha-Tarskiego mówi, że

Twierdzenie. Dla dowolnych dwóch ograniczonych podzbiorów 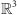$3 R$ o niepustym wnętrzu, jeden można tak podzielić na skończenie wiele części, by złożyć z nich drugi.

Można zatem podzielić sześcian na skończenie wiele fragmentów, a następnie zbudować z nich sześcian o objętości dwukrotnie większej. Wszystko dzięki temu, że "nożyczkami matematycznymi" (tym razem w wersji trójwymiarowej) da się wycinać przedziwne zbiory, także np. niemierzalne. Z takimi nożyczkami niemożliwe staje się możliwe!