Mała Delta
Pozbądźmy się koła

Dawno, dawno temu za górami, za lasami na Euklidesowych Równinach żyło sobie koło. Niezmiernie było dumne ze swej stałej szerokości. Chadzało ścieżkami, które miały szerokość równą jego średnicy, i jako jedyna figura zamieszkująca równiny mogło kręcić się przy tym jak szalone, stale podpierając obie krawędzie ścieżki.
Fakt, że jak dotąd żaden zamieszkujący równiny wielokąt nie miał obwodu równego obwodowi koła (problem znany jako wyprostowanie okręgu) - gdyż wszystkie one zostały stworzone jedynie przy użyciu cyrkla i linijki bez podziałki - napawał koło jeszcze większą dumą. I tak spacerowało kręcące się koło, przekonane o swej wyjątkowości.
Gdy w 1882 roku fakt niemożliwości kwadratury koła został udowodniony, dotknięty tym kwadrat wyznaczył nagrodę (w postaci matematycznej sławy) dla tego, kto jako pierwszy udowodni, że koło nie jest tak wyjątkowe, jak mu się wydaje. A koło było niezmiernie rade, że zainteresowanie nim rośnie...
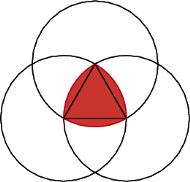
Konstrukcja trójkąta Reuleaux
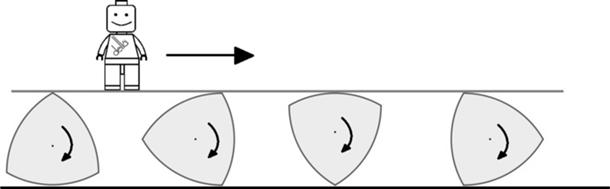
Wesprzyjmy kwadrat i poszukajmy figury, której szerokość (zdefiniowana na marginesie) jest stała niezależnie od kierunku, w jakim będzie mierzona (ang. curve of constant width). Bierzemy pod uwagę tylko figury wypukłe, ponieważ w innym przypadku koło z dowolnym otworem w środku spełniałoby nasze wymagania. Figurą, która zdobyła nagrodę wyznaczoną przez kwadrat, był trójkąt Reuleaux (od nazwiska jego twórcy). Żeby go otrzymać, skonstruuj trójkąt równoboczny, a następnie poprowadź łuk okręgu o środku w jednym z jego wierzchołków i promieniu równym długości boku trójkąta, łączący dwa pozostałe wierzchołki. Po powtórzeniu owej procedury w każdym z jego wierzchołków, otrzymasz zwycięską figurę. Żeby zrozumieć jej okrągłość, pomimo nie do końca okrągłego kształtu, wyobraźmy sobie deskę podpieraną przez te trójkąty. Podczas ich toczenia deska nie zmienia wysokości nad ziemią, nie następują "skoki", a znajdujący się na desce ludek nie jest w stanie rozpoznać, czy pod nim obracają się koła, czy zwycięskie trójkąty.
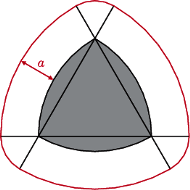
Trójkąt Reuleaux w otoczce o szerokości  ma teraz szerokość
ma teraz szerokość 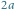 plus długość boku wyjściowego trójkąta.
plus długość boku wyjściowego trójkąta.
Figur z rodziny Reuleaux jest dużo więcej, kolejną będzie pięciokąt Reuleaux, siedmiokąt Reuleaux itd. (figury o nieparzystej liczbie łuków). Ich konstrukcja za każdym razem polega na zakreśleniu łuków okręgu pomiędzy sąsiadującymi wierzchołkami wielokąta foremnego o nieparzystej liczbie kątów, gdzie środkiem okręgu jest wierzchołek najbardziej oddalony od tego boku, a promień to najdłuższa przekątna. Drogi Czytelniku, samodzielnie wyznacz szerokości tych figur w zależności od długości boku wyjściowego wielokąta.
Tak uzyskane figury mają pewną cechę nie przez wszystkich uważaną za zaletę - mają rogi. Ale, oczywiście, rogów można się pozbyć. Wystarczy zrobić dla takiej rogatej figury otoczkę: dołączyć do niej wszystkie punkty odległe od niej nie więcej niż o dowolnie ustalony dystans - tak opatulona figura będzie miała gładki brzeg, a ponieważ w każdym kierunku przybędzie jej tyle samo, więc nadal będzie miała stałą szerokość.
Konstrukcja figury o stałej szerokości na bazie trójkąta o bokach 5, 4, 3; jeden z promieni przy 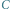 okazał się zerowy.
okazał się zerowy.
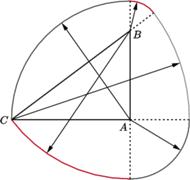
Figury o stałej szerokości można tworzyć na wiele różnych sposobów - oto jeszcze jeden, w którym za punkt wyjścia weźmiemy tym razem dowolny trójkąt o bokach 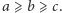 Niech
Niech 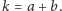 Kreślimy dwa łuki o środku w
Kreślimy dwa łuki o środku w 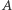 i promieniu
i promieniu  z tej strony, gdzie jest trójkąt oraz promieniu
z tej strony, gdzie jest trójkąt oraz promieniu 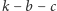 z przeciwnej strony. Podobnie kreślimy dwa łuki o środku
z przeciwnej strony. Podobnie kreślimy dwa łuki o środku 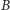 i promieniach
i promieniach  oraz
oraz 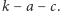 No i wreszcie rysujemy łuki o środku
No i wreszcie rysujemy łuki o środku 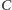 i promieniach
i promieniach 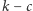 oraz
oraz 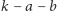 (czyli zero). Proszę spróbować: każdy dostrzeże, jak z tych łuków powstaje figura o stałej szerokości (jakiej?). Dla leniwych konkretny przykład jest na marginesie.
(czyli zero). Proszę spróbować: każdy dostrzeże, jak z tych łuków powstaje figura o stałej szerokości (jakiej?). Dla leniwych konkretny przykład jest na marginesie.
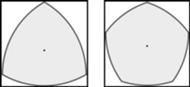
Figury o stałej szerokości obracają się bez luzu w kwadracie.
Do tej pory brzeg otrzymanych figur składał się z łuków okręgów. Można zbudować figurę o stałej szerokości niemającą na brzegu żadnego takiego łuku (ale to już robota dla zawodowców).

Figury z rodziny Reuleaux oraz monety w kształcie bardzo do nich zbliżonym - 50 pensów brytyjskich oraz jednodolarówka kanadyjska.
Figury o stałej szerokości można również zdefiniować na inne sposoby, na przykład:
- jest to figura, która, obracając się wewnątrz kwadratu, w dowolnym momencie dotyka każdego z jego boków (tj. obraca się w nim "bez luzu");
- jest to figura, do której nie można dołączyć ani jednego nowego punktu bez zwiększania jej szerokości.
Co ciekawe, wszystkie figury o stałej szerokości 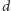 mają obwód równy
mają obwód równy 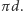 Mówiące o tym Twierdzenie Barbiera ubodło koło do kości. Czytelnika Wnikliwego odsyłamy do dowodu tegoż twierdzenia zawartego m.in. w Okruchach matematyki Jarosława Górnickiego. Wśród figur o danej szerokości największe pole ma koło, a najmniejsze trójkąt Reuleaux.
Mówiące o tym Twierdzenie Barbiera ubodło koło do kości. Czytelnika Wnikliwego odsyłamy do dowodu tegoż twierdzenia zawartego m.in. w Okruchach matematyki Jarosława Górnickiego. Wśród figur o danej szerokości największe pole ma koło, a najmniejsze trójkąt Reuleaux.

Chiński konstruktor Guan Baihua nie dał kołu za wygraną i w 2009 roku skonstruował rower o nieokrągłych kołach przystosowany do prostych dróg. Żeby rowerzysta mógł znajdować się na stałej wysokości nad ziemią, zmienił on konstrukcję roweru. Jego rama jest niejako położona na "kołach" (tak jak deska z ludkiem na trójkątach Reuleaux), a nie umocowana do osi obrotu koła jak w standardowym rowerze.
Możemy uznać, że figury o stałej szerokości zostały rozpracowane, a koło zdetronizowane. Może w takim razie udałoby się koło całkiem pozbawić wkładu w rzeczywistość i skonstruować nieokrągłe koło (dzięki czemu wszystkie używane w pojazdach koła można by zastąpić figurą o stałej szerokości). Przychodzące na myśl umiejscowienie osi obrotu w środku figury o stałej szerokości nie przyniesie oczekiwanego rezultatu. Rowerzysta na kołach w postaci trójkątów Reuleaux, nie znajdowałby się na stałej wysokości nad ziemią, co po dłuższej podróży mogłoby przyprawić go o mdłości. Podejmijmy próbę raz jeszcze: chcemy znaleźć nieokrągłe koła, w których odległość osi obrotu od poziomu (a tym samym rowerzysty od poziomu), byłaby stała - czyż to nie jest żywcem wzięta definicja okręgu? Mamy jednak pewne wyjście: czy zostały narzucone jakieś ograniczenia dotyczące podłogi? Nie!
Wybierzmy "koło" o dowolnym kształcie, na przykład kwadrat (żeby wzmocnić w nim poczucie własnej wartości) i skonstruujmy dla niego odpowiednią podłogę. Podłoga pomiędzy "wgłębieniami" ma kształt krzywej łańcuchowej, czyli taki jak, na przykład, zwisające przewody linii wysokiego napięcia (oczywiście, do góry nogami). Rowerzysta, mając taki kształt "kół" i jadąc po tej podłodze, będzie na stałej wysokości. Okazuje się, że dla dowolnego kształtu kół można skonstruować taką podłogę, żeby rowerzysta czuł się komfortowo. Jednak zdecydowanie lepiej jest (mimo wszystko) zostać przy standardowym okrągłym kształcie kół, niż modernizować trasy rowerowe, ulice i autostrady. Jednak jakieś uznanie dla koła mieć należy.

 ma teraz szerokość
ma teraz szerokość 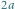 plus długość boku wyjściowego trójkąta.
plus długość boku wyjściowego trójkąta.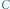 okazał się zerowy.
okazał się zerowy.