Deltoid
MI = MB = MC
Istnieje zaskakujący związek między okręgiem wpisanym w trójkąt i okręgiem na nim opisanym.
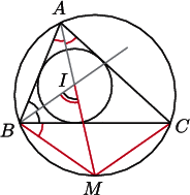
Twierdzenie. Dany jest trójkąt 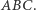 Punkt
Punkt 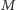 jest środkiem tego łuku
jest środkiem tego łuku 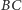 okręgu opisanego, do którego nie należy punkt
okręgu opisanego, do którego nie należy punkt 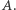 Wówczas punkt
Wówczas punkt 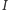 należący do odcinka
należący do odcinka 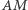 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 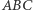 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 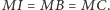
Dowód. Skoro 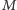 jest środkiem łuku
jest środkiem łuku 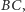 to
to 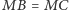 oraz
oraz 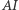 jest dwusieczną kąta
jest dwusieczną kąta 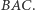 Wystarczy zatem dowieść, że
Wystarczy zatem dowieść, że 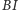 jest dwusieczną kąta
jest dwusieczną kąta 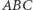 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 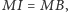 czyli gdy
czyli gdy 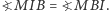
Kąt 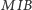 jest zewnętrzny w trójkącie
jest zewnętrzny w trójkącie 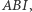 więc
więc 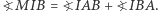 Z kolei
Z kolei 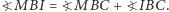 Ponieważ
Ponieważ 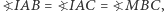 więc równość
więc równość 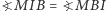 równoważna jest równości
równoważna jest równości 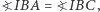 co kończy dowód.
co kończy dowód.