O obrotach centrów trójkąta
Zająłem się ciekawym problemem dotyczącym centrów trójkąta. Ciekawym, bo łatwym do wyobrażenia, a w pewnych aspektach nawet bardzo trudnym.

Najpierw wyjaśnienie, dlaczego napisałem "centrów", a nie zwyczajnie "środków" - chodzi tu o wspólną nazwę dla wszelkiego rodzaju wyróżnionych punktów związanych z trójkątem. Właściwie każdy punkt można jakoś wyróżnić - np. Clark Kimberling wyróżnił i opisał ich kilka tysięcy w swojej Encyclopedia of Triangle Centers. Tutaj "z imienia i nazwiska" będą przywołane: środek okręgu wpisanego jako 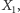 środek ciężkości jako
środek ciężkości jako 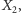 środek okręgu opisanego jako
środek okręgu opisanego jako 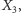 ortocentrum jako
ortocentrum jako 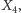 środek okręgu Feuerbacha (czyli dziewięciu punktów) jako
środek okręgu Feuerbacha (czyli dziewięciu punktów) jako 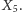
Na początek rozważmy wszystkie trójkąty równoramienne o wspólnej podstawie 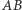 z wierzchołkiem
z wierzchołkiem 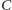 w danej półpłaszczyźnie ograniczonej prostą
w danej półpłaszczyźnie ograniczonej prostą 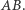 Dla ustalenia uwagi wprowadzimy prostokątny układ współrzędnych, w którym
Dla ustalenia uwagi wprowadzimy prostokątny układ współrzędnych, w którym 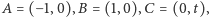
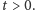 Interpretując
Interpretując 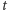 jako czas, możemy powiedzieć, że wierzchołek
jako czas, możemy powiedzieć, że wierzchołek 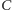 porusza się ruchem jednostajnym z prędkością 1 w górę, po symetralnej odcinka
porusza się ruchem jednostajnym z prędkością 1 w górę, po symetralnej odcinka 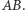 Po tej samej prostej poruszają się wymienione centra trójkąta
Po tej samej prostej poruszają się wymienione centra trójkąta 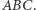 Skupimy się na razie na
Skupimy się na razie na 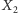 i
i 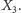 Póki
Póki 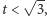 centrum
centrum 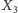 jest pod
jest pod 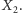 W chwili
W chwili 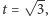 gdy trójkąt
gdy trójkąt 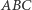 staje się równoboczny, centrum
staje się równoboczny, centrum 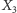 dogania
dogania 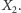 Dla
Dla 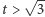 centrum
centrum 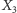 wychodzi na prowadzenie i potem już cały czas jest ponad
wychodzi na prowadzenie i potem już cały czas jest ponad 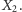 Nic dziwnego: w pogoni za
Nic dziwnego: w pogoni za 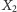 centrum
centrum 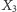 rozwinęło większą prędkość, więc po nieuchronnym zrównaniu musiało je wyprzedzić. Centra
rozwinęło większą prędkość, więc po nieuchronnym zrównaniu musiało je wyprzedzić. Centra 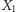 i
i 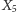 w chwili zrównania mają te same prędkości i nie następuje zmiana lidera.
w chwili zrównania mają te same prędkości i nie następuje zmiana lidera.
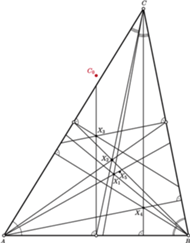
Zrezygnujmy teraz z założenia, że trójkąt 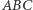 jest równoramienny, a niech trójkąt
jest równoramienny, a niech trójkąt 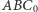 będzie równoboczny. Rozważmy problem: ile okrążeń wokół
będzie równoboczny. Rozważmy problem: ile okrążeń wokół 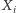 dokona centrum
dokona centrum 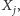 gdy wierzchołek
gdy wierzchołek 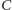 jednokrotnie okrąży punkt
jednokrotnie okrąży punkt 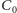 zgodnie z ruchem wskazówek zegara (wierzchołki
zgodnie z ruchem wskazówek zegara (wierzchołki 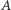 i
i 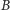 tkwią tam, gdzie poprzednio)? Z rozważań topologicznych (których nie będę tu przytaczał) wynika, że jeśli centra
tkwią tam, gdzie poprzednio)? Z rozważań topologicznych (których nie będę tu przytaczał) wynika, że jeśli centra 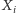 i
i 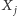 pokrywają się wyłącznie w trójkącie równobocznym, to odpowiedź na to pytanie nie zależy od konkretnego kształtu krzywej, po której wierzchołek
pokrywają się wyłącznie w trójkącie równobocznym, to odpowiedź na to pytanie nie zależy od konkretnego kształtu krzywej, po której wierzchołek 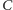 obiega punkt
obiega punkt 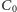 - możemy więc przyjąć, że krzywa ta jest okręgiem. Na małym okręgu wokół punktu
- możemy więc przyjąć, że krzywa ta jest okręgiem. Na małym okręgu wokół punktu 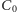 położonych jest dokładnie 6 punktów, z których każdy tworzy wraz z punktami
położonych jest dokładnie 6 punktów, z których każdy tworzy wraz z punktami 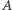 i
i 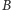 pewien trójkąt równoramienny. Dla tych sześciu punktów znamy kierunek wektora
pewien trójkąt równoramienny. Dla tych sześciu punktów znamy kierunek wektora 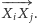 Nietrudno zgadnąć na tej podstawie, że
Nietrudno zgadnąć na tej podstawie, że 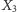 obiegnie jednokrotnie
obiegnie jednokrotnie 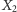 w kierunku przeciwnym do ruchu wskazówek zegara, natomiast
w kierunku przeciwnym do ruchu wskazówek zegara, natomiast 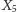 dwukrotnie okrąży
dwukrotnie okrąży 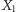 zgodnie z ruchem wskazówek.
zgodnie z ruchem wskazówek.
Wydaje się, że trzy obroty wektora 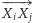 wokół
wokół 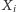 są wykluczone. Okazuje się jednak, że możliwe są cztery. W tym celu wskazałem odpowiednie dwa centra (inne od wymienionych - każdy może przecież zdefiniować swoje własne centra, nie ograniczając się nawet do encyklopedii Kimberlinga). Jak to zrobiłem, możesz dowiedzieć się tutaj, ale może najpierw sam spróbujesz?
są wykluczone. Okazuje się jednak, że możliwe są cztery. W tym celu wskazałem odpowiednie dwa centra (inne od wymienionych - każdy może przecież zdefiniować swoje własne centra, nie ograniczając się nawet do encyklopedii Kimberlinga). Jak to zrobiłem, możesz dowiedzieć się tutaj, ale może najpierw sam spróbujesz?