Drobiazgi

Czy potrafisz?

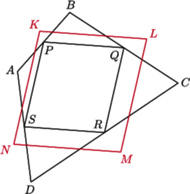
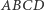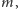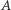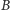Środek ciężkości wierzchołków czworokąta to środek równoległoboku, który tworzą środki jego boków. 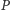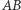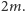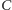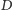Rzeczywiście, jeśli wierzchołki czworokąta $\text{[math]}$ obciążymy jednakowo ciężarami $\text{[math]}$ to środkiem ciężkości punktów $\text{[math]}$ i $\text{[math]}$ będzie środek $\text{[math]}$ odcinka $\text{[math]}$ obciążony przez $\text{[math]}$ Podobnie, środkiem ciężkości $\text{[math]}$ i $\text{[math]}$ będzie środek 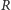$\text{[math]}$ odcinka 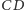$\text{[math]}$ obciążony przez 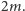$\text{[math]}$ Zatem środkiem ciężkości wszystkich wierzchołków będzie środek 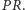$\text{[math]}$ Powtarzając to rozumowanie dla odcinków 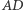$\text{[math]}$ i $\text{[math]}$ 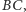stwierdzamy, że środkiem ciężkości wszystkich wierzchołków jest środek 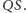$\text{[math]}$ Odcinki te mają więc wspólny środek, wobec tego czworokąt 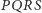$\text{[math]}$ jest równoległobokiem, a jego środek jest środkiem ciężkości wierzchołków czworokąta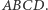 $\text{[math]}$

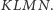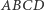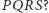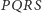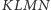Na rysunku jest jeszcze jeden równoległobok $\text{[math]}$ Powstał on z prostych przechodzących przez punkty dzielące boki czworokąta $\text{[math]}$ na trzy równe części. Czy potrafisz udowodnić, że jego boki są równoległe do boków równoległoboku $\text{[math]}$ - to nie powinno być trudne. Czy potrafisz wykazać, że środki równoległoboków $\text{[math]}$ i $\text{[math]}$ pokrywają się tylko wtedy, gdy 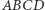$\text{[math]}$ też jest równoległobokiem? - to już trudniejsze. A czy potrafisz udowodnić, że środek 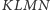$\text{[math]}$ jest środkiem ciężkości jednorodnej "deseczki" 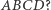$\text{[math]}$ - to jest już naprawdę trudne!