Deltoid

Twierdzenie Pascala

Delta, wrzesień 2014

o artykule ...

Publikacja w Delcie: wrzesień 2014
Publikacja elektroniczna: 01-09-2014
Wersja do druku [application/pdf]: (77 KB)

Tym razem o twierdzeniu Pascala...

Twierdzenie Pascala orzeka:

Twierdzenie. Jeśli jeśli sześciokąt 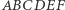$ABCDEF$ jest wpisany w okrąg, to punkty 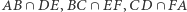$E,BCEF, AB$ są współliniowe, gdzie 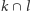$|k∩ l$ to punkt przecięcia prostych 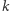$|k$ i $l.$

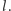
Jest ono prawdziwe również dla sześciokątów, których pewne boki się przecinają lub pewne wierzchołki pokrywają. Przez 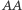$AA$ rozumiemy wtedy prostą styczną do rozważanego okręgu w punkcie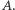 $A.$

W tym artykule zakładamy, że wszystkie rozważane punkty przecięcia prostych istnieją, ale Twierdzenia Pascala można uogólnić również na pozostałe przypadki. Ponadto, okrąg można zastąpić przez dowolną krzywą stożkową.

Narzędzia
Obiekty: Okręgi
Słowa kluczowe
Kategoria: Planimetria

Twierdzenie Pascala»Zadanie 1

o zadaniu...

Zadanie pochodzi z artykułu Twierdzenie Pascala
Publikacja w Delcie: wrzesień 2014
Publikacja elektroniczna: 01-09-2014
Artykuł źródłowy w wersji do druku [application/pdf]: (77 KB)

Okrąg wpisany w trójkąt $\text{[math]}$ jest styczny do boków $\text{[math]}$ odpowiednio w punktach $\text{[math]}$ Udowodnij, że punkty $\text{[math]}$ $\text{[math]}$ leżą na jednej prostej.

Rozwiązanie

Z Twierdzenia Pascala dla sześciokąta $\text{[math]}$ punkty $\text{[math]}$ oraz $\text{[math]}$ są współliniowe.

Narzędzia
Obiekty: Okręgi
Słowa kluczowe
Kategoria: Planimetria

Twierdzenie Pascala»Zadanie 2

o zadaniu...

Zadanie pochodzi z artykułu Twierdzenie Pascala
Publikacja w Delcie: wrzesień 2014
Publikacja elektroniczna: 01-09-2014
Artykuł źródłowy w wersji do druku [application/pdf]: (77 KB)

Na czworokącie $\text{[math]}$ który nie jest trapezem, opisano okrąg. Wykaż, że punkty $\text{[math]}$ leżą na jednej prostej.

Rozwiązanie

Niech $\text{[math]}$ Z Twierdzenia Pascala dla sześciokąta $\text{[math]}$ punkt $\text{[math]}$ leży na prostej wyznaczonej przez punkty $\text{[math]}$ oraz $\text{[math]}$ Z kolei z Twierdzenia Pascala dla $\text{[math]}$ punkt $\text{[math]}$ także leży na prostej wyznaczonej przez punkty $\text{[math]}$ oraz $\text{[math]}$

Narzędzia
Obiekty: Okręgi
Słowa kluczowe
Kategoria: Planimetria

Twierdzenie Pascala»Zadanie 3

o zadaniu...

Zadanie pochodzi z artykułu Twierdzenie Pascala
Publikacja w Delcie: wrzesień 2014
Publikacja elektroniczna: 01-09-2014
Artykuł źródłowy w wersji do druku [application/pdf]: (77 KB)

Punkty $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ leżą w tej kolejności na łuku okręgu $\text{[math]}$ Na odcinkach $\text{[math]}$ i $\text{[math]}$ wybrano takie punkty odpowiednio $\text{[math]}$ i $\text{[math]}$ że $\text{[math]}$ Wykaż, że wszystkie otrzymane w ten sposób proste $\text{[math]}$ (przy ustalonych punktach $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ) mają punkt wspólny.

Rozwiązanie

Z warunku $\text{[math]}$ wynika, że punkt $\text{[math]}$ leży na okręgu $\text{[math]}$ Z Twierdzenia Pascala dla sześciokąta $\text{[math]}$ uzyskujemy współliniowość punktów $\text{[math]}$ oraz niezależnego od $\text{[math]}$ i $\text{[math]}$ punktu $\text{[math]}$ co kończy dowód.

Narzędzia
Obiekty: Wielokąty
Słowa kluczowe
Kategoria: Planimetria

Twierdzenie Pascala»Zadanie 4

o zadaniu...

Zadanie pochodzi z artykułu Twierdzenie Pascala
Publikacja w Delcie: wrzesień 2014
Publikacja elektroniczna: 01-09-2014
Artykuł źródłowy w wersji do druku [application/pdf]: (77 KB)

Dany jest trójkąt $\text{[math]}$ w którym $\text{[math]}$ i takie punkty $\text{[math]}$ i $\text{[math]}$ w jego wnętrzu, że $\text{[math]}$ oraz $\text{[math]}$ Udowodnij, że punkty $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ są współliniowe.

Rozwiązanie

Oznaczmy $\text{[math]}$ oraz $\text{[math]}$ Z równoramienności trójkąta $\text{[math]}$ oraz danych równości kątów wynika, że $\text{[math]}$ Ponieważ oba punkty $\text{[math]}$ $\text{[math]}$ leżą po tej samej stronie prostej $\text{[math]}$ oznacza to, że punkty $\text{[math]}$ leżą na jednym okręgu.

Zadania domowe

Narzędzia
Obiekty: Okręgi
Słowa kluczowe
Kategoria: Planimetria

Twierdzenie Pascala»Zadanie 5

o zadaniu...

Zadanie pochodzi z artykułu Twierdzenie Pascala
Publikacja w Delcie: wrzesień 2014
Publikacja elektroniczna: 01-09-2014
Artykuł źródłowy w wersji do druku [application/pdf]: (77 KB)

Okrąg $\text{[math]}$ jest styczny do okręgu $\text{[math]}$ opisanego na trójkącie $\text{[math]}$ w punkcie $\text{[math]}$ a do boków $\text{[math]}$ i $\text{[math]}$ odpowiednio w punktach $\text{[math]}$ i $\text{[math]}$ Wykaż, że środek okręgu wpisanego w trójkąt $\text{[math]}$ jest środkiem odcinka $\text{[math]}$

Wskazówka

Niech proste $\text{[math]}$ $\text{[math]}$ przecinają okrąg $\text{[math]}$ odpowiednio w drugich punktach $\text{[math]}$ i $\text{[math]}$ Warto rozważyć Twierdzenia Pascala dla sześciokąta $\text{[math]}$

Narzędzia
Obiekty: Okręgi
Słowa kluczowe
Kategoria: Planimetria

Twierdzenie Pascala»Zadanie 6

o zadaniu...

Zadanie pochodzi z artykułu Twierdzenie Pascala
Publikacja w Delcie: wrzesień 2014
Publikacja elektroniczna: 01-09-2014
Artykuł źródłowy w wersji do druku [application/pdf]: (77 KB)

Punkt $\text{[math]}$ leży na boku $\text{[math]}$ pięciokąta wypukłego $\text{[math]}$ przy czym $\text{[math]}$ oraz $\text{[math]}$ Wykaż, że $\text{[math]}$

Wskazówka

Niech $\text{[math]}$

Zadanie (7). Uzasadnij poprawność konstrukcji opisanej w Małej Delcie w lutym 2014 r.

Obiekty: Bryły; Wielościany; Całki; Chaos; Fraktale; Ciągi liczbowe; Figury; Okręgi; Wielokąty; Funkcje; Grafy; Grupy; Gry; Konstrukcje; Krzywe; Liczby; Liczby naturalne; Liczby pierwsze; Liczby rzeczywiste; Liczby wymierne; Liczby zespolone; Losowość; Miary; Modele; Nierówności; Pochodne; Podzielność; Powierzchnie; Przekształcenia; Przestrzenie; Rachunki; Równania; Rozmaitości; Strategie; Szeregi liczbowe; Sztuczna inteligencja; Szyfrowanie; Węzły; Wielokąty; Wielomiany; Zbiory

Narzędzia: Indukcja; Jednokładności