Deltoid
Dwa w jednym
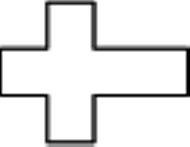
Powierzchnię pewnego wielościanu rozcięto (niekoniecznie wzdłuż krawędzi) i rozłożono, otrzymując płaski wielokąt o kształcie krzyża. Czy wyjściowy wielościan musiał być sześcianem?
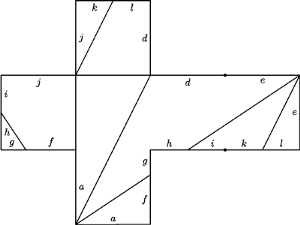
Okazuje się, że niekoniecznie. Jeśli figurę z rysunku 1a wyciąć, pozginać wzdłuż linii i skleić odcinki oznaczone tymi samymi literami, uzyskamy czworościan! Można się o tym przekonać praktycznie (proszę spróbować, najwygodniej na powiększonej kserokopii), można też teoretycznie, w następujący sposób.
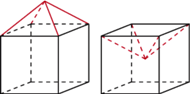
Rys. 2 Sześcian z daszkiem i sześcian z wnęką w kształcie daszka mają identyczne siatki.
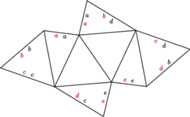
Rys. 3 Krawędzie oznaczone tymi samymi literami należy skleić. Kolorem oznaczono jeden z możliwych sposobów, na czarno – drugi. Warto skserować w powiększeniu, wyciąć i złożyć!
Odetnijmy kwadraty lewy i górny, a następnie doklejmy je do pozostałej części
wzdłuż odcinków oznaczonych literami
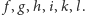 W efekcie
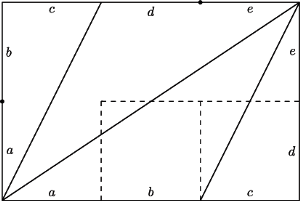
uzyskamy figurę z rysunku 1b — nietrudno sprawdzić, że jest to zwykła siatka
czworościanu — która po sklejeniu odpowiednich odcinków da tę samą
bryłę, co figura z rysunku 1a.
W efekcie
uzyskamy figurę z rysunku 1b — nietrudno sprawdzić, że jest to zwykła siatka
czworościanu — która po sklejeniu odpowiednich odcinków da tę samą
bryłę, co figura z rysunku 1a.
Powyższe podejście jest o tyle nietypowe, że dopuszcza cięcia w poprzek ścian. A czy można wielościan rozłożyć na siatkę i następnie złożyć z niej inny wielościan? Łatwo udzielić twierdzącej odpowiedzi, gdy zauważymy, iż rozważane wielościany nie muszą być wypukłe (Rys. 2).
Zażądajmy więc dodatkowo, by obydwa wielościany były wypukłe. Teraz odpowiedź jest mniej oczywista, ale również okazuje się pozytywna! Siatkę, z której można złożyć dwa różne wielościany wypukłe, przedstawia rysunek 3. Sekret tkwi w tym, że krawędzie tej siatki sklejamy na różne sposoby.
Dołączmy więc do naszych wymagań kolejny warunek: sklejać należy te same krawędzie siatki. Niestety (a może na szczęście?), tym razem nie istnieją szukane bryły, bowiem twierdzenie Cauchy’ego o sztywności orzeka, że siatka wraz z taką „instrukcją klejenia” jednoznacznie wyznacza wielościan wypukły.
Polecam animację Metamorphosis of the Cube