Symetria względem okręgu
W naszych rozważaniach wzbogacimy płaszczyznę o dodatkowy punkt, który
oznaczymy przez
 Przyjmiemy przy tym, że ów punkt leży na
każdej z prostych. Takie rozszerzone proste oraz okręgi obejmiemy wspólną
nazwą bloków...
Przyjmiemy przy tym, że ów punkt leży na
każdej z prostych. Takie rozszerzone proste oraz okręgi obejmiemy wspólną
nazwą bloków...
Czytelnik może wyobrażać sobie
 jako punkt „nieskończenie
daleko”, ale równie dobrze może traktować go jedynie jako umowę notacyjną,
która ułatwi sformułowanie pewnych zależności.
jako punkt „nieskończenie
daleko”, ale równie dobrze może traktować go jedynie jako umowę notacyjną,
która ułatwi sformułowanie pewnych zależności.

Kąt między krzywymi to kąt między stycznymi do nich w punkcie ich przecięcia.

Tak konstruuje się obraz punktu w symetrii względem prostej,

a tak względem okręgu.
Zacznijmy od zdefiniowania kąta między dwiema krzywymi: jeśli dwie gładkie krzywe się przecinają, to kątem między nimi nazwiemy kąt między stycznymi poprowadzonymi w punkcie przecięcia. W ogólności kąt ten może być różny dla różnych punktów przecięcia, tutaj jednak ograniczymy się wyłącznie do rozważania bloków. Dwa bloki mogą przecinać się w więcej niż jednym punkcie, ale wtedy otrzymany kąt nie zależy od jego wyboru; możemy więc śmiało mówić o kącie między dwoma przecinającymi się blokami. Gdy kąt ten jest prosty, figury nazywamy prostopadłymi. Na przykład, prosta jest prostopadła do okręgu dokładnie wtedy, gdy przechodzi przez jego środek.
Przypomnijmy dobrze znaną konstrukcję symetrii osiowej cyrklem i linijką.
Aby dla danej prostej
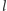 i punktu
i punktu
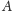 wyznaczyć punkt
wyznaczyć punkt
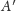 do niego symetryczny, zakreślamy dwa okręgi przechodzące przez
do niego symetryczny, zakreślamy dwa okręgi przechodzące przez
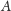 i prostopadłe do prostej
i prostopadłe do prostej
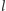 (czyli o środkach leżących na
(czyli o środkach leżących na
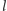 ). Wówczas punkt
). Wówczas punkt
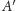 otrzymujemy jako drugi punkt przecięcia
tych okręgów. Oczywiście równie poprawne byłoby tutaj zastąpienie słowa
okrąg słowem blok. Jedyną zmianą byłoby dopuszczenie prostej przechodzącej
przez
otrzymujemy jako drugi punkt przecięcia
tych okręgów. Oczywiście równie poprawne byłoby tutaj zastąpienie słowa
okrąg słowem blok. Jedyną zmianą byłoby dopuszczenie prostej przechodzącej
przez
 i prostopadłej do
i prostopadłej do
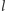 – co prawda trudniej jest ją wytyczyć,
ale przecież i ona przechodzi przez
– co prawda trudniej jest ją wytyczyć,
ale przecież i ona przechodzi przez
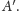 Tak sformułowany opis
konstrukcji motywuje do przeprowadzenia podobnej operacji w przypadku
okręgu.
Tak sformułowany opis
konstrukcji motywuje do przeprowadzenia podobnej operacji w przypadku
okręgu.
Definicja (symetria względem okręgu). Dany jest
okrąg
 oraz punkt
oraz punkt
 Poprowadźmy dwa bloki przechodzące
przez
Poprowadźmy dwa bloki przechodzące
przez
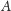 i prostopadłe do okręgu
i prostopadłe do okręgu
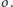 Ich drugi punkt przecięcia
Ich drugi punkt przecięcia
 nazwiemy punktem symetrycznym do
nazwiemy punktem symetrycznym do
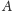 względem okręgu
względem okręgu
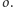 Otrzymane przekształcenie nazwiemy symetrią (lub inwersją)
względem okręgu
Otrzymane przekształcenie nazwiemy symetrią (lub inwersją)
względem okręgu

Jest jasne, że tak zdefiniowane przekształcenie jest samoodwrotne: obrazem
obrazu dowolnego punktu jest on sam. Powyższa definicja obejmuje również
przypadki, gdy
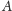 jest punktem
jest punktem
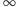 lub środkiem okręgu
lub środkiem okręgu
 Punkty te zamieniają się miejscami, gdyż wszystkie proste
przechodzące przez środek okręgu są prostopadłe do
Punkty te zamieniają się miejscami, gdyż wszystkie proste
przechodzące przez środek okręgu są prostopadłe do
 i przechodzą
przez punkt
i przechodzą
przez punkt

O symetrii względem okręgu (inwersji) można było przeczytać więcej m.in.
w deltoidzie 5/2013 i 8/2013. Definicja podana powyżej różni się
jednak od tej powszechnie przyjętej. Posiada ona niewątpliwe wady – nie
jest na przykład jasne, że określenie punktu
 nie zależy od
wyboru bloków prostopadłych. Czytelnik znający podstawowe własności
inwersji (można je znaleźć w przywołanych artykułach) może łatwo ze
standardowej definicji wyprowadzić powyższą jako wniosek. Nasza
definicja posiada jednak następującą zaletę – w naturalny sposób uogólnia
pojęcie symetrii osiowej. Tutaj pójdziemy na skróty, przywołując bez
dowodu najważniejsze własności symetrii względem ustalonego bloku
nie zależy od
wyboru bloków prostopadłych. Czytelnik znający podstawowe własności
inwersji (można je znaleźć w przywołanych artykułach) może łatwo ze
standardowej definicji wyprowadzić powyższą jako wniosek. Nasza
definicja posiada jednak następującą zaletę – w naturalny sposób uogólnia
pojęcie symetrii osiowej. Tutaj pójdziemy na skróty, przywołując bez
dowodu najważniejsze własności symetrii względem ustalonego bloku
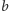 :
:
- (1)
- Obrazem dowolnego bloku jest blok.
- (2)
- Zachowane są kąty między krzywymi, w szczególności zachowana jest prostopadłość bloków.
- (3)
- Zachowane są symetrie względem bloków, to znaczy jeśli punkty
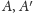 są symetryczne względem
są symetryczne względem
 to ich obrazy są
symetryczne względem obrazu
to ich obrazy są
symetryczne względem obrazu
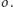
Gdy
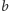 jest okręgiem o środku
jest okręgiem o środku
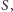 to punkty
to punkty
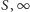 są
symetryczne względem
są
symetryczne względem
 Dlatego obrazem bloku przechodzącego przez
Dlatego obrazem bloku przechodzącego przez
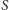 jest blok przechodzący przez
jest blok przechodzący przez
 czyli prosta. W podobny
sposób na podstawie własności 1 można podać kryteria, kiedy obrazem
prostej jest okrąg, kiedy obraz okręgu przechodzi przez
czyli prosta. W podobny
sposób na podstawie własności 1 można podać kryteria, kiedy obrazem
prostej jest okrąg, kiedy obraz okręgu przechodzi przez
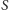 itd.
itd.
Zwróćmy uwagę, że trzecia własność wynika z dwóch poprzednich.
Istotnie, jeśli zgodnie z definicją mamy dwa bloki prostopadłe do
 przechodzące przez
przechodzące przez
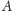 i
i
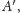 to przy symetrii
względem
to przy symetrii
względem
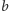 konfiguracja ta jest zachowana: ich obrazy są blokami
prostopadłymi do obrazu
konfiguracja ta jest zachowana: ich obrazy są blokami
prostopadłymi do obrazu
 i przechodzącymi przez obrazy punktów
i przechodzącymi przez obrazy punktów
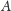 i
i
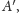 a zatem obrazy tych punktów są symetryczne względem
obrazu
a zatem obrazy tych punktów są symetryczne względem
obrazu
Poniżej znajdują się przykłady zadań, w których można z powodzeniem wykorzystać wymienione własności.
W drugiej części artykułu zaprezentuję wyjątkowo eleganckie twierdzenie, którego dowód wykorzystuje niektóre z przedstawionych wcześniej własności symetrii względem okręgu.
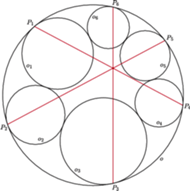
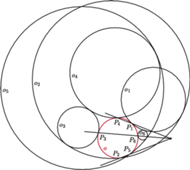
Twierdzenie (o siedmiu okręgach). Dany jest okrąg
 oraz styczne
do niego okręgi
oraz styczne
do niego okręgi
 z których każdy jest styczny do
następnego. Okrąg
z których każdy jest styczny do
następnego. Okrąg
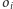 jest styczny do
jest styczny do
 w punkcie
w punkcie
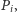 ponadto punkty
ponadto punkty
 leżą na
leżą na
 w tej właśnie kolejności. Wtedy
proste
w tej właśnie kolejności. Wtedy
proste
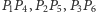 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
W dowodzie będziemy się posługiwać potęgą punktu względem okręgu. O tym przydatnym narzędziu można przeczytać w deltoidzie 2/2012 i 3/2012. Poniżej podajemy kluczowe dla nas własności i pojęcia.
Uwaga. Jeśli
dany jest okrąg
 i punkt
i punkt
 a prosta
a prosta
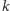 przechodzi
przez
przechodzi
przez
 i przecina
i przecina
 w punktach
w punktach
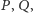 to wartość
iloczynu skalarnego
to wartość
iloczynu skalarnego
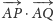 nie
zależy od wyboru prostej
nie
zależy od wyboru prostej
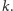 Tę wspólną wartość nazywamy
potęgą
Tę wspólną wartość nazywamy
potęgą
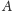 względem
względem
 . Dla dowolnych niewspółśrodkowych
okręgów
. Dla dowolnych niewspółśrodkowych
okręgów
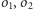 zbiór tych wszystkich punktów
zbiór tych wszystkich punktów
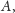 które
mają tę samą potęgę względem obu tych okręgów, tworzy prostą. Nazywamy
ją osią potęgową okręgów
które
mają tę samą potęgę względem obu tych okręgów, tworzy prostą. Nazywamy
ją osią potęgową okręgów
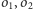 .
.
Jako przykład możemy rozważyć okręgi
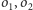 przecinające się
w punktach
przecinające się
w punktach
 Oba punkty mają tę samą (zerową) potęgę względem
obu okręgów, a zatem osią potęgową okręgów
Oba punkty mają tę samą (zerową) potęgę względem
obu okręgów, a zatem osią potęgową okręgów
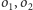 jest ich wspólna
sieczna
jest ich wspólna
sieczna
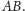 Ta obserwacja, choć bardzo prosta, okaże się nam jeszcze
przydatna.
Ta obserwacja, choć bardzo prosta, okaże się nam jeszcze
przydatna.
Lemat.
Dana jest prosta
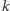 oraz okręgi
oraz okręgi
 z których każdy jest
styczny do następnego. Okrąg
z których każdy jest
styczny do następnego. Okrąg
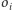 jest styczny do
jest styczny do
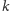 w punkcie
w punkcie
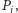 ponadto punkty
ponadto punkty
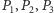 leżą na
leżą na
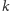 w tej właśnie
kolejności. Wtedy stosunek długości odcinków powstałych na prostej
w tej właśnie
kolejności. Wtedy stosunek długości odcinków powstałych na prostej
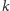 zależy wyłącznie od stosunku promieni okręgów
zależy wyłącznie od stosunku promieni okręgów
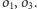
Lemat powyżej jest pozostawiony Czytelnikowi jako zadanie. Istotnie,
nietrudno jest obliczyć długości tych odcinków na podstawie promieni
okręgów
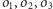 ; można też próbować mniej bezpośrednich
metod. Teraz możemy już przejść do właściwego dowodu.
; można też próbować mniej bezpośrednich
metod. Teraz możemy już przejść do właściwego dowodu.


Dowód twierdzenia. Podobnie jak w rozwiązaniu zadania 3,
przeprowadźmy symetrię względem dowolnego okręgu o środku
w
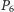 i obraz każdej z figur oznaczmy przez dodanie znaku prim.
Podobnie też możemy stwierdzić, że okręgi
i obraz każdej z figur oznaczmy przez dodanie znaku prim.
Podobnie też możemy stwierdzić, że okręgi
 i
i
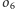 przechodzą
na proste równoległe
przechodzą
na proste równoległe
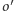 i
i
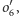 a obrazami pozostałych okręgów
są okręgi
a obrazami pozostałych okręgów
są okręgi
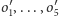 zachowujące odpowiednie styczności; ich promienie
oznaczmy kolejno przez
zachowujące odpowiednie styczności; ich promienie
oznaczmy kolejno przez
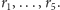 W szczególności oba okręgi
W szczególności oba okręgi
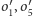 są styczne do prostych równoległych
są styczne do prostych równoległych
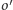 i
i
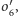 zatem
zatem
 Punkty styczności
Punkty styczności
 leżą na prostej
leżą na prostej
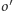 w tej
właśnie kolejności.
w tej
właśnie kolejności.
Proste
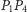 i
i
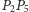 przechodzą na okręgi
przechodzą na okręgi
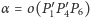 i
i
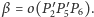 Pozostaje wykazać, że prosta
Pozostaje wykazać, że prosta
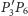 (czyli obraz prostej
(czyli obraz prostej
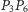 ) przechodzi przez drugi punkt
przecięcia
) przechodzi przez drugi punkt
przecięcia
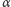 i
i
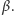 Na podstawie stwierdzenia i następującej po nim
uwagi jest to równoważne temu, że punkt
Na podstawie stwierdzenia i następującej po nim
uwagi jest to równoważne temu, że punkt
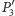 leży na osi potęgowej
leży na osi potęgowej
 i
i
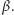 Aby to sprawdzić, wystarczy pokazać równość
Aby to sprawdzić, wystarczy pokazać równość
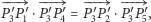 która przy ustalonej przez nas kolejności
punktów
która przy ustalonej przez nas kolejności
punktów
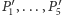 przyjmuje postać proporcji
przyjmuje postać proporcji

Lemat implikuje, że lewa strona równości wyraża się przez stosunek
promieni
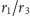 ; podobnie prawa strona wyraża się w ten sam sposób
przez
; podobnie prawa strona wyraża się w ten sam sposób
przez
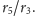 Już wcześniej zauważyliśmy, że
Już wcześniej zauważyliśmy, że
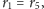 co
kończy dowód.
co
kończy dowód.
Na koniec chciałbym zachęcić Czytelnika do zastanowienia się nad poniższymi pytaniami. Wydają się one całkiem naturalne, a w celu znalezienia odpowiedzi wystarczy prześledzić powyższy dowód.
- Jak sformułować twierdzenie, aby można było w nim mówić
o dowolnych blokach
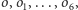 niekoniecznie okręgach?
niekoniecznie okręgach?
- Jakie inne kolejności punktów
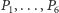 na okręgu
na okręgu
 można dopuścić w założeniach?
można dopuścić w założeniach?