Mała Delta
Rozety

Wikipedia
Rozeta z kościoła St-Jean-de-Malte w Aix-en-Provence
Jednym z najbardziej charakterystycznych elementów architektury średniowiecznej, zwłaszcza gotyckiej, są rozety. Są to okrągłe okna z delikatną konstrukcją kamienną, których puste przestrzenie są najczęściej wypełnione witrażami. Pierwsze rozety pojawiają się już w kościołach romańskich; zamiast witrażami są wypełnione cienkimi płytkami kamiennymi, przepuszczającymi światło.
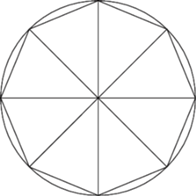
Nas nie będzie interesować sposób wypełnienia tych pustych przestrzeni, ale geometryczny wzór konstrukcji kamiennej, dzielącej rozetę na części. Na rysunku 1 widzimy jedną z najprostszych rozet romańskich, wzorowaną na rozecie z prowansalskiego opactwa Silvacane. Na rysunku 2 widzimy, w jaki sposób ta rozeta powstała. Dostrzegamy znajome elementy: ciągi kolejno stycznych zewnętrznie okręgów, stycznych wewnętrznie do dużego okręgu. Dostrzegamy również podobny element: ciąg takich okręgów stycznych zewnętrznie do mniejszego okręgu. Takie ciągi kolejno stycznych okręgów były podstawowym elementem konstrukcji wieloliści. W jednym z poprzednich artykułów omówiliśmy trzy rodzaje wieloliści i obliczyliśmy długości promieni tych okręgów oraz odległości środków tych promieni od środka największego okręgu. W tym artykule zobaczymy, jak w ogólnym przypadku można skonstruować te okręgi.

Rys. 4

Rys. 5
Rys. 6

Rys. 7

Rys. 8
Zaczynamy od podziału koła na równe wycinki. Końce promieni tworzących te wycinki są wierzchołkami wielokąta foremnego wpisanego w okrąg (zob. rysunek 3). W tym momencie powstaje problem, w jaki sposób możemy skonstruować wielokąt foremny wpisany w okrąg. Od starożytności znane są konstrukcje niektórych wielokątów foremnych: trójkąta, kwadratu, pięciokąta, sześciokąta, ośmiokąta, dziesięciokąta i wielu innych. Dzisiaj wiemy również, że niektóre wielokąty foremne (np. siedmiokąt czy dziewięciokąt) nie są konstruowalne za pomocą cyrkla i linijki; znane są natomiast konstrukcje przybliżone. Nie będziemy w tym artykule zajmować się dokładniej kwestią podziału koła na równe części. Takie podziały wykonywano cyrklem i linijką, metodami przybliżonymi lub też metodą prób i błędów, osiągając zadowalającą dokładność.
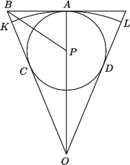
Nas będzie interesować skonstruowanie okręgu wpisanego w wycinek i dopisanego do wycinka. Okręgiem wpisanym w wycinek koła nazywamy okrąg styczny do trzech linii ograniczających wycinek: obu promieni i łuku tworzącego ten wycinek (zob. rysunek 4). Okręgiem dopisanym do wycinka koła nazywamy okrąg styczny do łuku tworzącego ten wycinek i przedłużeń obu promieni (zob. rysunek 5).
Zajmiemy się najpierw okręgiem wpisanym w wycinek koła. Przypuśćmy, że
taki okrąg jest już skonstruowany. Jest on styczny do łuku
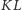 oraz do
promieni
oraz do
promieni
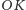 i
i
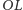 (zob. rysunek 6). Ze względu na symetrię
okrąg wpisany jest styczny do łuku
(zob. rysunek 6). Ze względu na symetrię
okrąg wpisany jest styczny do łuku
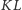 w jego środku
w jego środku
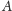 ;
środek okręgu wpisanego leży przy tym na promieniu
;
środek okręgu wpisanego leży przy tym na promieniu
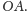 Niech
punkty
Niech
punkty
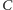 i
i
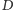 będą punktami styczności okręgu wpisanego
z promieniami dużego okręgu. Poprowadźmy wspólną styczną do obu
okręgów w ich punkcie styczności
będą punktami styczności okręgu wpisanego
z promieniami dużego okręgu. Poprowadźmy wspólną styczną do obu
okręgów w ich punkcie styczności
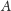 i niech
i niech
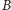 będzie punktem
przecięcia tej stycznej z prostą
będzie punktem
przecięcia tej stycznej z prostą
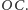 Zauważmy, że środek
Zauważmy, że środek
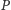 okręgu wpisanego leży na dwusiecznej kąta
okręgu wpisanego leży na dwusiecznej kąta
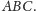 Widzimy
zatem sposób konstrukcji punktu
Widzimy
zatem sposób konstrukcji punktu
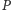 :
:
- prowadzimy dwusieczną kąta tworzącego wycinek,
- punkt przecięcia tej dwusiecznej z łukiem ograniczającym wycinek
oznaczamy literą
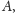
- przez punkt
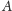 prowadzimy prostą prostopadłą do
dwusiecznej
prowadzimy prostą prostopadłą do
dwusiecznej
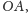
- literą
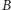 oznaczamy punkt przecięcia tej prostopadłej
z przedłużeniem promienia tworzącego wycinek,
oznaczamy punkt przecięcia tej prostopadłej
z przedłużeniem promienia tworzącego wycinek,
- prowadzimy dwusieczną kąta
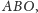
- literą
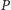 oznaczamy punkt przecięcia dwusiecznej kąta
oznaczamy punkt przecięcia dwusiecznej kąta
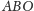 z promieniem
z promieniem
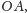
- rysujemy okrąg
o środku w punkcie
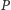 i promieniu
i promieniu
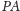 ; punktami
styczności
; punktami
styczności
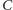 i
i
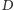 narysowanego okręgu wpisanego
z promieniami tworzącymi wycinek są rzuty punktu
narysowanego okręgu wpisanego
z promieniami tworzącymi wycinek są rzuty punktu
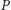 na te
promienie.
na te
promienie.

Rys. 9

Rys. 10
Konstrukcja okręgu dopisanego do wycinka jest bardzo podobna (zob.
rysunek 7). Przypuśćmy, że dany jest już okrąg dopisany styczny do
przedłużeń promieni w punktach
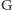 i
i
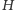 oraz do łuku
oraz do łuku
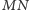 w punkcie
w punkcie
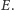 Znów ze względu na symetrię punkt
Znów ze względu na symetrię punkt
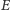 jest środkiem łuku
jest środkiem łuku
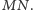 Zauważmy następnie, że środek
okręgu dopisanego jest punktem przecięcia półprostej
Zauważmy następnie, że środek
okręgu dopisanego jest punktem przecięcia półprostej
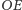 z dwusieczną
kąta
z dwusieczną
kąta
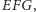 którą możemy łatwo skonstruować. Obie konstrukcje
zostały pokazane na rysunku 8 Linią pogrubioną zostały zaznaczone łuki
okręgów zewnętrznego i wewnętrznego, łuki okręgów wpisanego i dopisanego
będące fragmentami rozety z Silvacane i łączące je odcinki promieni. Należy tu
jeszcze dodać, że wielkość najmniejszego okręgu była dobierana
dowolnie przez artystę tworzącego rozetę, zgodnie z jego wyczuciem
estetycznym.
którą możemy łatwo skonstruować. Obie konstrukcje
zostały pokazane na rysunku 8 Linią pogrubioną zostały zaznaczone łuki
okręgów zewnętrznego i wewnętrznego, łuki okręgów wpisanego i dopisanego
będące fragmentami rozety z Silvacane i łączące je odcinki promieni. Należy tu
jeszcze dodać, że wielkość najmniejszego okręgu była dobierana
dowolnie przez artystę tworzącego rozetę, zgodnie z jego wyczuciem
estetycznym.
Za pomocą opisanych wyżej konstrukcji można utworzyć wiele różnych rozet. Pozostawimy Czytelnikowi jako ćwiczenie skonstruowanie dwóch pięknych rozet. Pierwsza z nich pochodzi z kościoła St-Jean-de-Malte w Aix-en-Provence w południowej Francji (rysunek 9), druga z katedry w Troia w południowych Włoszech (rysunek 10). Ta druga rozeta jest szczególnie interesująca z tego powodu, że występuje w niej niezwykle rzadko spotykany podział koła na 11 wycinków. Ponieważ jedenastokąt foremny nie może być skonstruowany za pomocą cyrkla i linijki, więc od Czytelnika oczekujemy konstrukcji przybliżonej podziału okręgu na 11 równych części (np. metodą prób i błędów) i następnie skonstruowania widocznych 11 łuków. W tej rozecie zwróćmy także uwagę na ostrołuki powstające z przecięcia łuków okręgów. Ostrołuki występujące w rozetach będą tematem następnego artykułu.