Twierdzenie Morleya
Każdy wie, co to są dwusieczne kątów – tutaj będziemy mówili o trójsiecznych, czyli prostych dzielących kąt (i jego kąt wierzchołkowy) na trzy równe częsci. Zatem trójsieczne są dwie. Mają one dziwną własność zwaną twierdzeniem Morleya.
Rys. 1
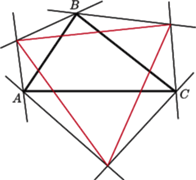
Twierdzenie (Morleya). Punkty przeciecięcia tych trójsiecznych kątów trójkąta, które sąsiadują z którymś z boków trójkąta, są wierzchołkami trójkąta równobocznego(Rys. 1).
Dowieść można go np. tak. Niech trójsieczne kątów przy wierzchołkach
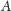 i
i
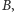 sąsiadujące z
sąsiadujące z
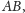 przecinają się w punkcie
przecinają się w punkcie
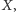 a pozostałe trójsieczne tych kątów w punkcie
a pozostałe trójsieczne tych kątów w punkcie
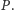 Po obu
stronach odcinka
Po obu
stronach odcinka
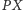 odłóżmy kąt
odłóżmy kąt
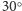 o wierzchołku
o wierzchołku
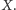 Przecięcia ramion tego kąta z
Przecięcia ramion tego kąta z
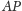 i
i
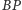 oznaczmy,
odpowiednio, przez
oznaczmy,
odpowiednio, przez
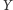 i
i
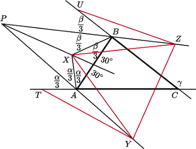
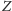 (Rys. 2). Wykażemy, że trójkąt
(Rys. 2). Wykażemy, że trójkąt
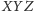 jest równoboczny i proste
jest równoboczny i proste
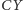 i
i
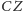 są
trójsiecznymi kąta przy wierzchołku
są
trójsiecznymi kąta przy wierzchołku
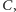 co zakończy dowód
twierdzenia.
co zakończy dowód
twierdzenia.
W tym celu zauważmy najpierw, że
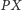 jest dwusieczną kąta
jest dwusieczną kąta
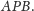 Wynika to z faktu, że
Wynika to z faktu, że
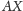 i
i
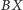 są dwusiecznymi,
odpowiednio, kątów
są dwusiecznymi,
odpowiednio, kątów
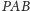 i
i
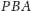 trójkąta
trójkąta
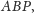 a trzy
dwusieczne kątów trójkąta przecinają się w jednym punkcie. Okazało się
więc, że czworokąt
a trzy
dwusieczne kątów trójkąta przecinają się w jednym punkcie. Okazało się
więc, że czworokąt
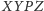 jest deltoidem, z czego wynika, że
jest deltoidem, z czego wynika, że
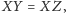 co dowodzi, że trójkąt
co dowodzi, że trójkąt
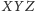 jest równoramienny.
jest równoramienny.
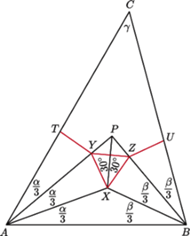
Rys. 2
Ponadto mamy też
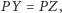 a skoro tak, to
a skoro tak, to

Oznaczmy teraz obrazy symetryczne punktu
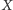 względem prostych
względem prostych
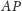 i
i
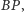 odpowiednio, przez
odpowiednio, przez
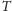 i
i
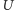 (oczywiście,
leżą one na
(oczywiście,
leżą one na
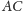 i
i
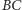 ). Mamy więc
). Mamy więc
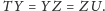

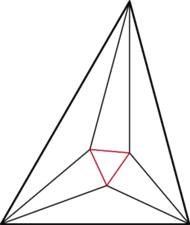
Rys. 3
Ponieważ
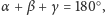 więc
więc

Podobnie
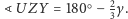 Na podstawie równości tych kątów
i ich ramion można stwierdzić, że punkty
Na podstawie równości tych kątów
i ich ramion można stwierdzić, że punkty
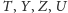 leżą na jednym
okręgu (Rys. 3). Jego środkiem jest mianowicie punkt
leżą na jednym
okręgu (Rys. 3). Jego środkiem jest mianowicie punkt
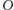 przecięcia
dwusiecznych kątów
przecięcia
dwusiecznych kątów
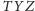 i
i
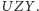 Każdy z odcinków
Każdy z odcinków
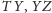 i
i
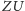 jest cięciwą odpowiadającą kątowi środkowemu
jest cięciwą odpowiadającą kątowi środkowemu
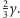 Ponieważ rozwartość kąta
Ponieważ rozwartość kąta
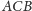 (czyli
(czyli
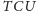 ) jest
równa
) jest
równa
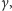 więc punkt
więc punkt
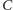 leży również na tym samym
okręgu, a kąty
leży również na tym samym
okręgu, a kąty
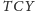 i
i
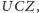 jako równe połowom kątów
jako równe połowom kątów
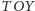 i
i
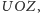 mają rozwartość
mają rozwartość
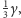 co kończy
dowód.
co kończy
dowód.
W sformułowaniu twierdzenia nie było mowy o tym, że chodzi o kąty
wewnętrzne, choć z tego korzystałem – rzecz w tym, że twierdzenie Morleya
jest prawdziwe również dla kątów zewnętrznych i ma praktycznie taki sam
dowód (trzeba tylko pamiętać, że suma kątów zewnętrznych jest równa
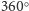 ). Poniżej są rysunki do tego dowodu.
). Poniżej są rysunki do tego dowodu.