Odpowiedź jest pozytywna, a rozwiązujący podawali (i uzasadniali), że warunki spełnia np. trójkąt równoramienny o długości podstawy 30 i ramion po 25. Wtedy wysokość opuszczona na podstawę ma długość 20, a na każde z ramion po 24. Zwykle dochodzono do tego, odbijając symetrycznie trójkąt prostokątny o bokach długości 3, 4 i 5 względem dłuższej przyprostokątnej. Otrzymuje się wtedy trójkąt równoramienny o długości podstawy 6 i ramion po 5, a wysokości, odpowiednio, 4 i dwie po 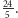 Kąt przy podstawie jest, oczywiście, ostry, a kąt między ramionami jest mniejszy niż 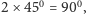 gdyż jest równy podwojonemu mniejszemu kątowi w trójkącie prostokątnym (leży naprzeciw krótszej przyprostokątnej). Jest to zatem trójkąt ostrokątny, w którym żądane długości są liczbami wymiernymi. Wystarczało teraz powiększyć go pięciokrotnie (jednokładnie względem któregoś wierzchołka w skali 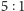), aby otrzymać odpowiedź.

Analizując powyższy przykład, widzimy, że istotne było w nim znalezienie takiego trójkąta ostrokątnego, w którym żądane długości są liczbami wymiernymi i do tego posłużył trójkąt prostokątny o bokach długości 3, 4 i 5. Jest to najmniejszy trójkąt prostokątny, którego długości boków 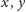 i   tworzą tzw. trójkę pitagorejską 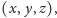 czyli są liczbami naturalnymi spełniającymi równanie

Równanie to ma nieskończenie wiele rozwiązań, a wszystkie trójki pitagorejskie wyrażają się wzorami

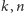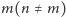gdzie  i   są liczbami naturalnymi. Przypomnijmy też, że w trójce pitagorejskiej musi być 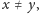 gdyż 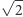 jest liczbą niewymierną.

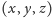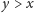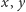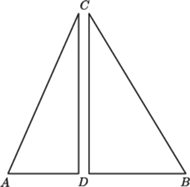
Powstaje pytanie, czy dla dowolnej trójki pitagorejskiej  analogiczna konstrukcja prowadzi do trójkąta ostrokątnego o wymaganych w zadaniu własnościach. Odpowiedź też jest pozytywna. Załóżmy, że  i odbijmy symetrycznie trójkąt prostokątny o bokach długości  i   względem dłuższej przyprostokątnej. 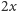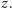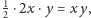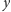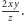Wtedy otrzymuje się trójkąt równoramienny o podstawie długości  i ramion po  Pole tego trójkąta wynosi  zatem wysokości mają długości, odpowiednio,  i   Uzasadnienie, że jest to trójkąt ostrokątny, jest analogiczne. Wystarczy teraz powiększyć ten trójkąt  razy, aby otrzymać pozytywną odpowiedź.

Trudniejsza jest sprawa, gdy pytamy o trójkąt ostrokątny o żądanych w zadaniu własnościach, ale niekoniecznie równoramienny. W tym przypadku odpowiedź też jest pozytywna, a poszukiwanie trójkąta o żądanych własnościach również opiera się na opisanym wyżej motywie. Weźmy dwie różne trójki pitagorejskie 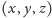 i 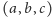  i niech 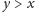 oraz 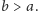 Rozważmy trójkąty prostokątne 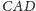 i 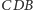  o bokach długości: 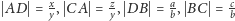 oraz 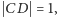 gdzie 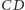 jest w nich wspólną, dłuższą z przyprostokątnych.

Zauważmy, że w trójkącie 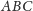 boki mają długośc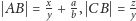i:  i   Pole tego trójkąta wynosi 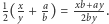 Wysokości mają długości, odpowiednio,

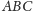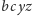są więc liczbami wymiernymi. Zatem w trójkącie  długości wszystkich boków i wysokości są wymierne. Powiększając więc go  razy (jednokładnie względem któregoś wierzchołka), otrzymujemy trójkąt o żądanych własnościach.