Współcześnie na papierowych mapach nawigacyjnych nadal niejednokrotnie wykonuje się różne konstrukcje geometryczne i w części odbywa się to w sposób klasyczny, tzn. za pomocą cyrkla i linijki.

W XX wieku na licznych morskich i lotniczych mapach nawigacyjnych można było znaleźć dodatkowo naniesioną siatkę linii hiperbolicznych związanych z wykorzystaniem w celu pozycjonowania naziemnych systemów radionawigacyjnych, jak np. Decca, Omega, Chayka, Loran. Ten ostatni nadal funkcjonuje na Dalekim Wschodzie na akwenach Pacyfiku, a transmisja jego stacji nadawczych, znajdujących się w Ameryce Północnej, została zakończona całkiem niedawno, tj. w sierpniu 2010 roku.

Zasada działania systemu hiperbolicznego opiera się na pomiarze różnic czasu lub faz odbieranych sygnałów z par stacji nadawczych. Przy ustalonej prędkości propagacji różnicę czasu możemy zamienić na różnicę odległości. Ponieważ hiperbola składa się z punktów, których wartość bezwzględna różnicy odległości od dwóch ustalonych punktów (ognisk) jest stała, więc miejsca, w których jest ustalona stała różnica czasu między dwoma sygnałami, mogą być przedstawione graficznie jako linia pozycyjna w kształcie hiperboli.

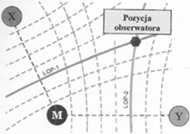
Rys. 1 Zasada określenia pozycji w oparciu o hiperboliczne linie pozycyjne (gdzie M, X, Y – stacje nadawcze; LOP – linia pozycyjna, ang. line of position).

Oczywiście, odbiór sygnałów od dwóch nadajników nie może posłużyć do jednoznacznego określenia pozycji obserwatora, a jedynie jednej linii pozycyjnej – hiperboli, na której pozycja obserwatora się znajduje. Odbiornik systemu powinien więc odbierać i obliczać także różnice czasu pomiędzy drugą parą stacji nadawczych. Pozwala to na określenie pozycji obserwatora w punkcie przecięcia dwóch hiperbol wykreślonych na mapie, co poglądowo przedstawiono na rysunku 1.

Rys. 2 Siatki hiperbolicznych linii pozycyjnych na nawigacyjnej mapie morskiej.

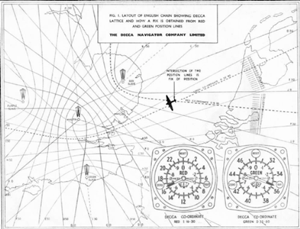
Rys. 3 Siatki hiperbolicznych linii pozycyjnych na nawigacyjnej mapie lotniczej.

Jedna para stacji generuje rodzinę hiperbol o tych samych ogniskach – właśnie w ogniskach znajdują się pozycje stacji nadawczych. W praktyce jedna ze stacji pierwszej pary może być wykorzystywana zarazem jako stacja w drugiej parze, zatem niezbędne są co najmniej trzy stacje. Najczęściej wykorzystuje się jednak zsynchronizowane sygnały nadawane z czterech stacji, co pozwala w danej chwili wyznaczyć trzy linie pozycyjne. Stacje naziemne pracują w grupach (tzw. łańcuchach) trzech lub czterech stacji. W danym łańcuchu jedna ze stacji pełni rolę nadrzędną i nazywana jest stacją główną (ang. master, na rysunku M), a pozostałe określa się jako podrzędne. Linia pozycyjna jest wyznaczana na podstawie sygnałów ze stacji głównej i podrzędnej. Stacje te oddalone są o 1100-1500 km. Wyznaczenie punktu przecięcia dwóch hiperbolicznych linii pozycyjnych na mapie z naniesioną siatką hiperbol (Rys. 2 i Rys. 3), generowanych przez łańcuchy systemu, pozwala w efekcie na wyznaczenie współrzędnych geograficznych pozycji obserwatora.

W późniejszej fazie rozwoju systemu wykorzystano odbiorniki śledzące w sposób ciągły sygnał układu i automatycznie przekształcające odbierane sygnały na współrzędne geograficzne pozycji obserwatora (statku, samolotu), czas, prędkość, a także dobierające automatycznie i optymalnie łańcuchy stacji w celu poprawy jakości określania pozycji, np. dokładności, ciągłości. Bezwzględna dokładność systemu Loran-C wynosiła 0,10-0,25 mil morskich (około 185-463 m).

Unowocześniona wersja systemu, występująca pod nazwą eLoran (ang. enhanced Loran), charakteryzuje się zwiększoną dokładnością określania pozycji (wynoszącą około 10 m), co jest wynikiem ulepszenia odbiornika oraz charakterystyki transmisji. Stacje systemu eLoran zostały także wykorzystane do transmisji dodatkowych sygnałów, w szczególności poprawek DGPS (ang. Differential Global Positioning System) w celu poprawy dokładności i wskazań urządzeń różnicowej odmiany satelitarnego systemu GPS.

W zastosowaniach morskich systemy hiperboliczne wykorzystywano w żegludze przybrzeżnej, jak również w nawigacji dalekiego zasięgu (nazwa systemu Loran pochodzi od ang. LOng RAnge Navigation) przy odległościach statku rzędu kilkuset mil morskich od stacji nadawczych.

Zauważmy, iż do tej pory zakładaliśmy bezzasadnie, że mamy do czynienia ze zwyczajnymi, to jest płaskimi hiperbolami, że wszystko dzieje się na płaszczyźnie. Jednak przy wspomnianym wyżej rzędzie wielkości w celu uzyskania pomiarów o większej dokładności należy uwzględnić krzywiznę Ziemi. Na przykład, aproksymując sferyczny trójkąt równoboczny o długości boku 400 km przez trójkąt płaski, popełniamy błąd około 232 km  Namiar radionawigacyjny globalnie nie może być rozważany jako euklidesowa linia prosta na płaszczyźnie, ale jako linia geodezyjna powierzchni, na której de facto się znajduje. Jeżeli używamy w modelowaniu globalnym sfery, to linia taka jest łukiem okręgu wielkiego.

Spróbujmy zatem zastanowić się nad własnościami krzywych stożkowych, w szczególności hiperbol, na sferze wykorzystywanej w uproszczonym modelowaniu powierzchni Ziemi.

Krzywe stożkowe (okrąg, elipsa, hiperbola, parabola) na płaszczyźnie są dobrze znane i możemy ich obecność zaobserwować w licznych zastosowaniach, np. w fizyce. Ich definicji możemy formalnie użyć w innych strukturach geometrycznych, np. na zakrzywionych powierzchniach, i tam spróbować znaleźć ich odpowiedniki. Na początek spróbujmy przyjrzeć się własnościom elipsy i hiperboli na powierzchni kuli 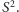 A więc szukamy linii, których punkty są określone przez warunek stałości sumy odległości od ognisk (w przypadku elipsy) bądź modułu różnicy odległości od ognisk (w przypadku hiperboli).

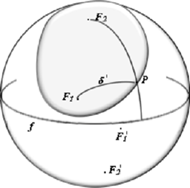
Rys. 4

Niech ogniskami będą dwa punkty jednostkowej sfery,  i   których sferyczna (czyli mierzona po powierzchni kuli) odległość 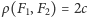 spełnia warunek 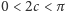– pierwsze ograniczenie po to, by były różne, drugi – by nie były antypodyczne. Przyjrzyjmy się leżącej na sferze figurze, której punkty spełniają, dla pewnego dodatniego 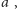 warunek wynikający z nierówności trójkąta

(*)

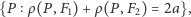który na płaszczyźnie, przy 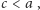 określałby elipsę. Na sferze należy ten warunek wzmocnić do 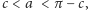 gdyż na sferze odległości nie przekraczają 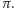 Figurę tę przedstawia rysunek 4.

Na tym rysunku są zaznaczone także punkty  i 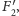  antypodyczne do 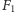 i 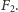  Oczywiście, dla dowolnego punktu 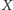 mamy 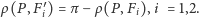 Zatem figurę opisaną przez 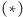 można opisać również jako

W ten sposób sferyczna elipsa okazała się również sferyczną hiperbolą, tyle że o innych ogniskach.

Rys. 5 Siatka współrzędnych zbudowana ze współogniskowych i przecinających się pod kątem prostym elips i hiperbol.

Jednakże hiperbole i elipsy, odnoszące się do tej samej pary ognisk, nie są takimi samymi krzywymi. Tak jak na płaszczyźnie (Rys. 5), przecinają się one pod kątem prostym. Analogicznym układem można się posługiwać na sferze – układ taki, ze względu na nieodróżnialność sferycznych elips i hiperbol nazywa się eliptycznym.

Okazuje się także, że istnieje naturalny związek między sferyczną elipsą/hiperbolą a trzecią przedstawicielką krzywych stożkowych – parabolą. W płaskiej geometrii euklidesowej parabola to zbiór punktów o równej odległości od ustalonej prostej (kierownicy) oraz ustalonego punktu (ogniska) nieleżącego na kierownicy. Na sferze punkt 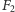 wyznacza jednoznacznie swój punkt antypodyczny 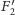 oraz symetralną 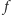 odcinka 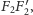 która jest okręgiem wielkim leżącym w odległości 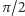 od tych punktów (a więc geodezyjną, czyli sferyczną prostą). Można zobaczyć to w ten sposób, że okrąg 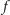 ma dwa środk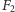i,  i 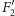 – tak jak równik i dwa bieguny sfery z nim związane.

Rys. 6 Sferyczne krzywe stożkowe – wygląd przybliżony, wersja sportowa.

Rozważmy zbiór wszystkich punktów na sferze równoodległych od danego punktu 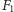 i sferycznej prostej 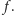 Jest on sferyczną parabolą o ognisku 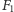 i kierownicy 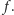 Pozostawiam Czytelnikowi sprawdzenie, że oba warunki:

określają również sferyczną parabolę (Rys. 4).

W ten sposób otrzymaliśmy krzywą, która jest jednocześnie sferyczną elipsą, hiperbolą i parabolą. Używając takiej samej definicji dla stożkowych na płaszczyźnie jak i na sferze, widzimy, że sytuacja geometrycznie jest zasadniczo inna w obydwu przypadkach.

Przedstawiona sferyczna krzywa stożkowa (a nawet można by powiedzieć – trzy krzywe w jednej) nie ma specjalnej nazwy, choć, być może, na nią zasługuje ze względu na ciekawe własności, jakie ma. Pozostawiając Czytelnikowi wymyślenie własnej nazwy dla przedstawionej tu krzywej, proponuję nazwę, która już się pojawiła w tytule artykułu: odpowiednio zestawiając ze sobą pierwsze litery nazw stożkowych, w  „skóry” których owa krzywa wchodzi, powstaje akronim peh (od parabola – elipsa – hiperbola), a co za tym idzie, nazwa „pehowa” krzywa, choć wcale na pechową nie wygląda.

Reasumując, można wykazać, że na sferze każda elipsa jest hiperbolą i odwrotnie, a czasem bywa także parabolą. Dodatkowo, gdy kierownica 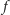pokrywa się z równikiem sfery i 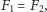  parabola sferyczna jest równoleżnikiem o szerokości geograficznej 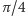(czyli 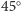), więc jest także szczególnym przypadkiem okręgu sferycznego.

***

W artykule został użyty model sfery 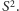 W praktyce dokładniejsze i bardziej wiarygodne wyniki obliczeń geodezyjno-kartograficznych uzyskalibyśmy, gdyby przyjąć jako model Ziemi elipsoidę obrotową (nazywaną także sferoidą) lub elipsoidę trójosiową. Krzywe stożkowe można również rozważać na innych zakrzywionych powierzchniach lub w ogólniejszych strukturach geometrycznych, gdzie ich „wygląd” i własności mogą nieraz zaskakiwać.

Z geometrycznego punktu widzenia można powiedzieć, iż w nawigacji istotę stanowi wyznaczenie dwóch wielkości: odległości i kąta. Różne struktury geometryczne dostarczają różnych narzędzi i stwarzają różne możliwości. W szczególności, na rozmaitości Riemanna istnieje możliwość obliczania odległości i kąta, a w ogólniejszej strukturze, za jaką uważa się rozmaitość Finslera, istnieje możliwość obliczania odległości, ale kąta już nie. Ale o tym może innym razem.