Okrąg dziewięciu punktów i pewne dwa fakty
Trzy niewspółliniowe punkty na płaszczyźnie jednoznacznie wyznaczają okrąg, który przez nie przechodzi. Zatem jeśli pewne cztery punkty leżą na jednym okręgu, to jest to fakt godny odnotowania. W geometrii istnieje niezwykle urocze twierdzenie, które mówi, że aż dziewięć szczególnych punktów trójkąta leży na jednym okręgu.
Twierdzenie. Dany jest trójkąt
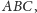 a punkt
a punkt
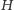 to jego
ortocentrum. Punkty
to jego
ortocentrum. Punkty
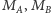 i
i
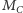 są środkami boków
są środkami boków
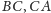 i
i
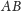 tego trójkąta,
tego trójkąta,
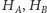 i
i
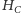 to
spodki wysokości poprowadzonych odpowiednio z wierzchołków
to
spodki wysokości poprowadzonych odpowiednio z wierzchołków
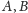 i
i
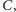 zaś
zaś
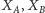 i
i
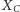 to środki odcinków
to środki odcinków
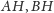 i
i
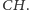 Wówczas
punkty
Wówczas
punkty
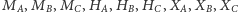 leżą na jednym okręgu
zwanym okręgiem dziewięciu punktów.
leżą na jednym okręgu
zwanym okręgiem dziewięciu punktów.
W literaturze istnieje kilka różnych dowodów tego twierdzenia. Oto szkic najpopularniejszego z nich – uzupełnienie szczegółów może być ciekawym ćwiczeniem dla Czytelników, którzy go nie znają.
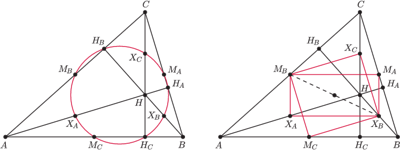
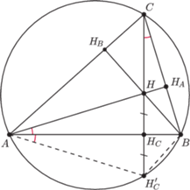
Rys. 1
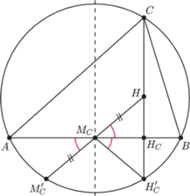
Rys. 2
Dowód. Zauważmy, że
czworokąty
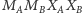 oraz
oraz
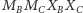 są prostokątami
o wspólnej przekątnej
są prostokątami
o wspólnej przekątnej
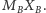 Oznacza to, że ich wierzchołki leżą
na okręgu o środku w środku odcinka
Oznacza to, że ich wierzchołki leżą
na okręgu o środku w środku odcinka
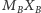 (ten punkt jest
także środkiem każdej z pozostałych przekątnych tych prostokątów).
Pozostaje jeszcze zauważyć, że każdy z trójkątów
(ten punkt jest
także środkiem każdej z pozostałych przekątnych tych prostokątów).
Pozostaje jeszcze zauważyć, że każdy z trójkątów
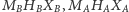 i
i
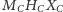 jest prostokątny.
jest prostokątny.
Czytelnik Odważny z łatwością sprawdzi, że ten dowód bez kłopotów przenosi się na wyższe wymiary i istnieje odpowiednik okręgu dziewięciu punktów w dowolnym wymiarze. W przestrzeni trójwymiarowej jest to dobrze znana sfera dwunastu punktów.
Okazuje się, że okrąg dziewięciu punktów wiąże się ściśle z dwoma dobrze znanymi prostymi faktami.
Fakt 1. Punkt
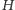 jest punktem przecięcia wysokości trójkąta
jest punktem przecięcia wysokości trójkąta
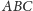 (Rys. 1).
Prosta
(Rys. 1).
Prosta
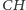 przecina bok
przecina bok
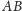 w punkcie
w punkcie
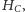 zaś okrąg
opisany na trójkącie
zaś okrąg
opisany na trójkącie
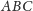 w punkcie
w punkcie
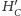 (różnym od
(różnym od
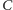 ). Wówczas punkt
). Wówczas punkt
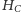 jest środkiem odcinka
jest środkiem odcinka
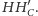 (W skrócie: ortocentrum trójkąta w symetrii względem jego
boków ląduje na okręgu opisanym.)
(W skrócie: ortocentrum trójkąta w symetrii względem jego
boków ląduje na okręgu opisanym.)
Dowód. Zauważmy, że

i podobnie
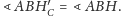 W takim razie punkty
W takim razie punkty
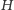 i
i
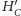 są
symetryczne względem odcinka
są
symetryczne względem odcinka
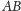 oraz
oraz
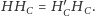
Fakt 2. Punkt
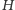 jest punktem przecięcia wysokości
trójkąta
jest punktem przecięcia wysokości
trójkąta
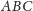 (Rys. 2). Niech
(Rys. 2). Niech
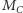 będzie środkiem boku
będzie środkiem boku
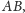 zaś
zaś
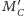 punktem
przecięcia półprostej
punktem
przecięcia półprostej
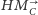 z okręgiem opisanym na trójkącie
z okręgiem opisanym na trójkącie
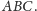 Wtedy
Wtedy
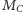 jest środkiem odcinka
jest środkiem odcinka
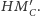
Dowód. Z poprzedniego faktu wnosimy, że

co oznacza, że proste
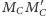 i
i
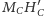 są symetryczne
względem symetralnej odcinka
są symetryczne
względem symetralnej odcinka
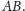 Z drugiej strony symetralna ta
jest również osią
symetrii okręgu opisanego na trójkącie
Z drugiej strony symetralna ta
jest również osią
symetrii okręgu opisanego na trójkącie
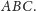 To zaś oznacza, że
punkty
To zaś oznacza, że
punkty
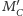 i
i
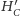 również są względem niej symetryczne.
Stąd i z poprzedniego faktu mamy:
również są względem niej symetryczne.
Stąd i z poprzedniego faktu mamy:
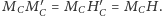
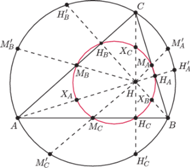
Teraz możemy w zaskakująco prosty sposób udowodnić twierdzenie o okręgu dziewięciu punktów.
Dowód. Analogicznie do punktów
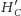 i
i
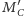 definiujemy
punkty
definiujemy
punkty
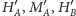 oraz
oraz
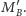 Odnotujmy, że:
Odnotujmy, że:
- punkty
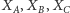 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
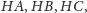
- punkty
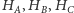 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
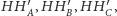
- punkty
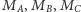 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
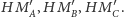
Rozważmy teraz jednokładność o środku w punkcie
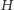 o skali
o skali
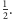 Z powyższych obserwacji wnioskujemy więc, że przy tej
jednokładności:
Z powyższych obserwacji wnioskujemy więc, że przy tej
jednokładności:
- punkty
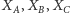 są odpowiednio obrazami punktów
są odpowiednio obrazami punktów
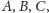
- punkty
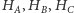 są odpowiednio obrazami punktów
są odpowiednio obrazami punktów
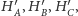
- punkty
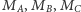 są odpowiednio obrazami punktów
są odpowiednio obrazami punktów
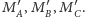
Jednakże punkty
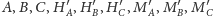 leżą na jednym okręgu,
zatem ich obrazy również.
leżą na jednym okręgu,
zatem ich obrazy również.
To, że powyższego dowodu nie widziałem nigdzie w literaturze, wydaje mi się dość zaskakujące, bowiem fakt, iż okrąg dziewięciu punktów jest obrazem jednokładnym okręgu opisanego w rozważanej w dowodzie jednokładności, jest bardzo dobrze znany. Jedynie Michał Szurek w Opowieściach geometrycznych wykorzystuje w podobny sposób fakt 1, ale tamten dowód nie jest tak prosty. To właśnie za jego pomocą dowodzi się, że środek okręgu dziewięciu punktów leży na prostej Eulera i jest środkiem odcinka łączącego ortocentrum ze środkiem okręgu opisanego na danym trójkącie.
Co ciekawe, powyższe rozumowanie można odwrócić (rozważając jednokładność odwrotną do opisanej) i za pomocą okręgu dziewięciu punktów udowodnić dwa przytoczone fakty, a więc okrąg dziewięciu punktów jest z nimi równoważny.
Czytelnik Wnikliwy od razu zauważy, że w ten sposób można otrzymać odpowiedniki faktów 1 i 2 w przestrzeni, zaś Czytelnik Odważny sprawdzi to również w wyższych wymiarach. Czy można je jednak otrzymać inną drogą, co pozwoliłoby na uzyskanie z nich sfery dwunastu punktów? Okazuje się, że tak. Przestrzenny odpowiednik faktu 1 był jednym z zadań na finale LXII Olimpiady Matematycznej. Jedna z kilku możliwych metod przeprowadzenia dowodu to dwukrotne zastosowanie faktu 1 oraz wykorzystanie kilku własności czworościanów ortocentrycznych. To rozumowanie można także zastosować w indukcyjnym dowodzie dla wyższych wymiarów, co z pewnością zainteresuje Czytelnika Odważnego. Przestrzenny odpowiednik faktu 2 udowodnić jest nieco trudniej, bowiem poza przestrzenną wersją faktu 1 należy wykorzystać jeszcze prostą Eulera dla trójkąta będącego podstawą czworościanu. Czytelnik Odważny w celu uogólnienia tego faktu na wyższe wymiary będzie musiał wykorzystać odpowiednik prostej Eulera podany na marginesie.