Konkurs prac uczniowskich
Japońska geometria świątynna
Połączenie matematyki z religią może wydawać się nam, Europejczykom, dość zaskakujące. W Japonii jednak przez bardzo długi czas nie było niczym niezwykłym. Zjawisko to zostało zapoczątkowane w XVII wieku, kiedy władcy tego kraju podjęli decyzję o zamknięciu portów i odcięciu Japonii od reszty świata, szczególnie od Europy Zachodniej, a trwało do XIX wieku.
W tym czasie w Kraju Kwitnącej Wiśni nastąpił znaczny rozwój kultury, sztuki i nauki – także matematyki. Do dziś zachowało się wiele eksponatów pochodzących ze świątyń Shinto, obowiązującej wówczas religii. Są to drewniane tabliczki z kolorowymi rysunkami, przedstawiającymi ułożone na różne sposoby figury geometryczne. Szczególnie wiele jest tam okręgów stycznych do różnych figur, często do innych okręgów. Te obrazki to sangaku – w dosłownym tłumaczeniu „matematyczne tabliczki”.
Sangaku to w istocie zadania z geometrii euklidesowej. Część z nich nie ma nawet polecenia – odgadnięcie go jest częścią zagadki. Inne jednak opisano w Kanbun, czyli piśmie używającym ideogramów chińskich, a czytanym po japońsku. Kanbun miał podobną rangę jak łacina na Zachodzie, był językiem ludzi mających wyższe wykształcenie. Stąd wniosek, że tworzyli i rozwiązywali te sangaku głównie obywatele z klasy samurajów. Cele tworzenia sangaku były dwojakie: wysiłek włożony w rozwiązanie ofiarowywano opiekuńczym duchom, a wisząca w świątyni tabliczka stawała się wyzwaniem dla innych.
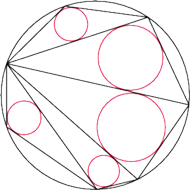
Rys. 1
Prawdopodobnie najbardziej znanym na Zachodzie sangaku pozostaje tzw. japońskie twierdzenie o wielokącie wpisanym w okrąg, występujące nawet pod nazwą „sangaku” w Kąciku olimpijskim (zob. [1]).
Sangaku 1. Suma promieni okręgów wpisanych we wszystkie trójkąty pewnej triangulacji wielokąta wpisanego w okrąg jest stała dla danego wielokąta i niezależna od triangulacji (Rys. 1).
Dowód tego twierdzenia także znajduje się w Kąciku olimpijskim, nie będę go więc tu przytaczać.
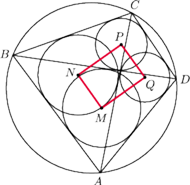
Rys. 2
Jedno sangaku pojawiło się nawet na Asian Pacific Mathematics Olympiad w 1996 r. Znane jest ono jako japońskie twierdzenie o czworokącie wpisanym w okrąg.
Sangaku 2. Czworokąt
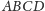 jest wpisany w okrąg. Wówczas
środki
jest wpisany w okrąg. Wówczas
środki
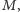
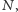
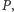
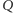 okręgów wpisanych odpowiednio
w trójkąty
okręgów wpisanych odpowiednio
w trójkąty
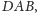
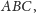
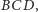
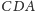 tworzą
prostokąt (Rys. 2).
tworzą
prostokąt (Rys. 2).
Przy dowodzie tego twierdzenia najpierw wykazujemy, że na
czwórkach punktów złożonych z dwóch środków okręgów
wpisanych i dwóch odpowiednio do nich dobranych wierzchołków
czworokąta (np. na czwórce
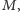
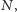
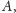
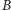 )
można opisać okrąg. Następnie bierzemy dwa takie okręgi (np.
opisane na punktach
)
można opisać okrąg. Następnie bierzemy dwa takie okręgi (np.
opisane na punktach
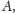
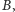
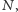
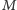 oraz
oraz
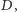
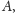
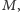
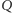 ) i wykazujemy, że odpowiedni kąt
(w naszym przykładzie kąt
) i wykazujemy, że odpowiedni kąt
(w naszym przykładzie kąt
 ) jest kątem prostym. Całość dowodu
to proste rachunki na kątach w okręgu, które pozostawiam Czytelnikowi
do sprawdzenia.
) jest kątem prostym. Całość dowodu
to proste rachunki na kątach w okręgu, które pozostawiam Czytelnikowi
do sprawdzenia.
Rys. 3
Rys. 4
Rys. 5
Aby ukazać specyfikę zadań sangaku, przedstawię tu rozwiązanie jednego z nich w całości.
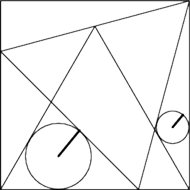
Sangaku 3. Dane są dwa trójkąty równoboczne wpisane w kwadrat oraz dwa okręgi wpisane w wybrane z powstałych trójkątów, jak pokazuje rysunek 3. Należy znaleźć zależność między promieniami tych okręgów.
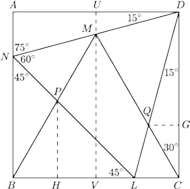
Przyjmijmy oznaczenia wierzchołków i punktów przecięcia odcinków jak
na rysunku 4. Weźmy ponadto punkty
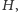
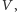
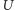 i
i
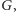 będące rzutami prostokątnymi, odpowiednio, punktu
będące rzutami prostokątnymi, odpowiednio, punktu
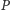 na
na
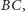
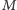 na
na
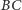 i
i
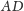 oraz
oraz
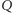 na
na
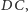 i oznaczmy znane kąty. Bez straty ogólności możemy
przyjąć, że długości boków kwadratu są równe
i oznaczmy znane kąty. Bez straty ogólności możemy
przyjąć, że długości boków kwadratu są równe
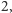 czyli
czyli
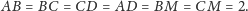 Wtedy wysokość
Wtedy wysokość
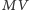 trójkąta równobocznego
trójkąta równobocznego
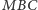 ma długość
ma długość
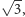 a zatem
a zatem
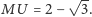 Z podobieństwa trójkątów
Z podobieństwa trójkątów
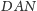 oraz
oraz
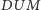 mamy
mamy
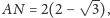 stąd
stąd
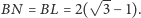
Obliczymy teraz długości promieni zaznaczonych okręgów. Będziemy
korzystać ze wzoru
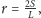 gdzie
gdzie
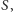
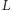 i
i
 to
odpowiednio pole trójkąta, jego obwód i promień okręgu wpisanego.
Aby uprościć te obliczenia, wykonamy je dla okręgów wpisanych
w trójkąty podobne do
to
odpowiednio pole trójkąta, jego obwód i promień okręgu wpisanego.
Aby uprościć te obliczenia, wykonamy je dla okręgów wpisanych
w trójkąty podobne do
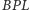 oraz
oraz
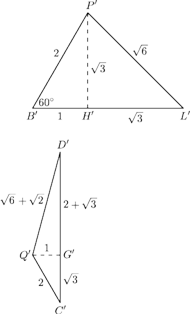
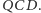 Rozważmy
trójkąty
Rozważmy
trójkąty
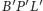 oraz
oraz
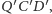 takie że
takie że
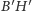 oraz
wysokość
oraz
wysokość
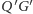 mają długość 1, jak na rysunku 5. Wtedy promień
mają długość 1, jak na rysunku 5. Wtedy promień
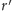 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt
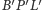 ma długość
ma długość

Promień
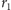 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt
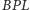 ma się do
ma się do
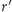 tak, jak
tak, jak
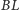 do
do
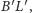 a ponieważ
a ponieważ

więc

Analogicznie obliczamy

Po wykonaniu kilku przekształceń dochodzimy do wniosku, że
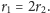
Jest to jedno z bardziej typowych sangaku. Jak widać, rozwiązanie zawiera parę pomysłów i raczej żmudne obliczenia, ale nie korzysta z wyszukanych metod i nie wymaga niczego więcej niż podstawowa wiedza z zakresu planimetrii.
W Delcie 9/2011 w artykule Stowarzyszenia na rzecz Edukacji Matematycznej można przeczytać o twierdzeniu Caseya. Przypomnę w tym miejscu jego uproszczoną wersję, gdyż posłuży nam ona do rozwiązania następnego sangaku.
Twierdzenie (Twierdzenie Caseya). Jeśli
okręgi
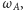
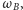
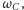
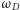 są styczne do okręgu
są styczne do okręgu
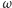 w punktach
w punktach
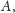
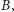
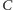 i
i
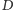 (wszystkie wewnętrznie lub wszystkie zewnętrznie) oraz czworokąt
(wszystkie wewnętrznie lub wszystkie zewnętrznie) oraz czworokąt
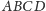 wpisany w okrąg
wpisany w okrąg
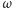 jest wypukły, to spełniona jest
równość:
jest wypukły, to spełniona jest
równość:

gdzie
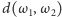 to długość odcinka między punktami styczności
okręgów
to długość odcinka między punktami styczności
okręgów
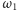 i
i
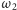 do ich wspólnej zewnętrznej stycznej.
do ich wspólnej zewnętrznej stycznej.
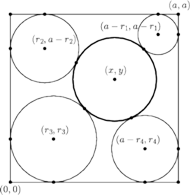
Rys. 6
Sangaku 4. Wewnątrz
kwadratu o boku długości
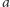 znajduje się okrąg
znajduje się okrąg
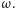 Okrąg
ten nie ma punktów wspólnych z brzegiem kwadratu. Cztery okręgi
Okrąg
ten nie ma punktów wspólnych z brzegiem kwadratu. Cztery okręgi
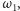
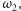
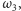
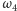 o różnych promieniach są
styczne do okręgu
o różnych promieniach są
styczne do okręgu
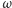 oraz każdy z nich jest styczny do dwóch boków
kwadratu (Rys. 6). Wyznacz długość boku kwadratu w zależności od
promieni okręgów
oraz każdy z nich jest styczny do dwóch boków
kwadratu (Rys. 6). Wyznacz długość boku kwadratu w zależności od
promieni okręgów
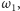
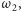
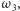
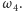
Zadanie to najłatwiej rozwiązać, zapisując równość wynikającą z twierdzenia Caseya. Długości interesujących nas odcinków można wyznaczyć, używając twierdzenia Pitagorasa i odejmując długości odpowiednich promieni od długości boku kwadratu. W ten sposób otrzymujemy równanie
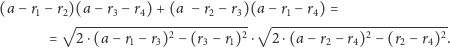 | (1) |
 pozostaje jedynie kwestią
sprawności rachunkowej.
pozostaje jedynie kwestią
sprawności rachunkowej.
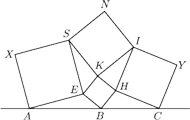
Rys. 7
Na koniec sangaku dość nietypowe, bowiem niezawierające ani jednego okręgu. Czytelnik Wnikliwy z pewnością zechce je rozwiązać w ramach rozwijania znajomości z japońskimi zadaniami geometrycznymi.
Sangaku 5. Dane są cztery kwadraty
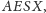
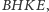
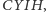
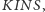 ułożone jak
na rysunku 7. Jaka jest zależność
między polami kwadratów
ułożone jak
na rysunku 7. Jaka jest zależność
między polami kwadratów
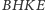 oraz
oraz
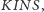 jeśli punkty
jeśli punkty
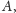
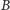 i
i
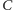 są współliniowe?
są współliniowe?
Podpowiedź: można wpisać kwadraty, do których należą wierzchołki
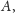
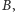
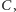 w kwadraty o podstawach zawierających się
w prostej
w kwadraty o podstawach zawierających się
w prostej