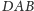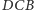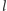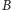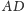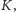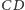Podstawowy pomysł polega na podziale kąta  na takie dwie części, że kąty „bliższe” kątom  i  są im odpowiednio równe. Pozwala na to podana w zadaniu równość kątów. Aby zrealizować powyższy pomysł, należy dorysować prostą  przechodzącą przez punkt  i przecinającą bok  w punkcie  a bok  w punkcie 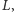 tak by trójkąty 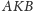 i 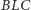 były równoramienne. 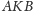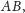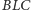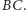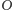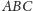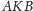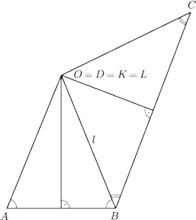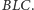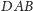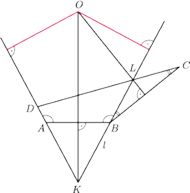Wtedy dwusieczna kąta  jest symetralną boku  a dwusieczna kąta  – symetralną boku  Oznacza to, że środek  okręgu opisanego na trójkacie  leży na przecięciu dwusiecznych kątów  i  W sytuacji, gdy kąty  i  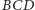są ostre, możliwe są trzy przypadki przedstawione na rysunkach 1, 2 i 3.

Rys. 4

Rys. 5

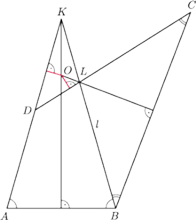
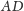W przypadkach 2 i 3 punkt  jest środkiem okręgu wpisanego w trójkąt  gdyż leży na przecięciu dwusiecznych. Jest on więc jednakowo odległy od prostych  i 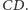 Żaden z uczniów rozwiązujących to zadanie nie rozważył sytuacji, gdy trójkąta 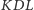 po prostu nie ma, bądź jeden z kątów 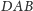 lub 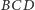 nie jest ostry. Trójkąt 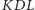 nie powstaje, gdy 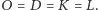 Ale wtedy teza jest oczywista, bo żądane odległości są równe 0.

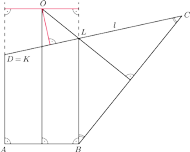
Pozostają do rozważenia konfiguracje, w których jeden z kątów 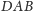 lub 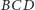 jest rozwarty lub prosty. W tej pierwszej sytuacji załóżmy, bez zmniejszania ogólności, że rozwarty jest kąt 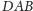 (rysunek 4). Wtedy punkt 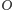 jest środkiem okręgu dopisanego do trójkąta 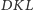 i stąd wynika teza.

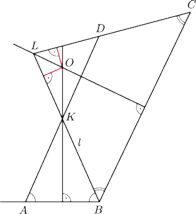
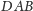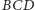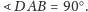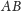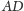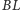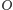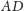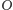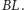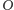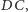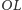Najtrudniejszy do rozważenia jest przypadek, gdy jeden z kątów  lub  jest prosty (rysunek 5). Załóżmy np., że  Wtedy symetralna boku  jest równoległa do prostych  i  i równo od nich odległa. W takim razie odległość punktu  od prostej  jest taka sama, jak odległość punktu  od prostej  Ta ostatnia odległość jest z kolei równa odległości punktu  od prostej  gdyż  jest również dwusieczną kąta wierzchołkowego do 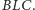 To spostrzeżenie kończy rozwiązanie zadania.