Mała Delta
O sadzeniu drzew
Girard DESARGUES, matematyk, architekt ogrodów, doradca kardynała Richelieu (a więc rówieśnik Atosa, Portosa i Aramisa) postawił kolegom ogrodnikom pytanie: Jak posadzić 10 drzew w dziesięciu rzędach po 3 drzewa w każdym rzędzie?
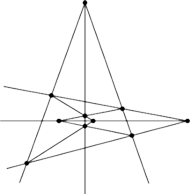
Rys. 1
I kiedy oni doszli do wniosku, że widać matematycy nie są całkiem normalni, przedstawił im widoczne obok rozwiązanie.
Natomiast kolegom matematykom wytłumaczył, że taka możliwość bierze się stąd, iż żyjemy w trójwymiarowej przestrzeni. Można bowiem – patrząc uważnie na ten rysunek – dopatrzyć się w nim czworościanu przeciętego płaszczyzną.
* * *
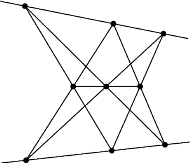
Rys. 2
Zasłyszawszy o tym, Blaise PASCAL, matematyk, fizyk, filozof, bezbożnik i teolog, konstruktor arytmometru, wynalazca taczek, i tak dalej, i dalej..., człowiek szalenie ambitny, postanowił, że zmierzy się z trudniejszym pytaniem:
Jak posadzić 9 drzew w dziewięciu rzędach po 3 drzewa w każdym rzędzie?
I faktycznie pokazał, jak te drzewa trzeba posadzić – rysunek jest obok.
Każdy z nas może wykonać oba te rysunki, bo wykonuje się je „byle jak” – należy po prostu rysować po kolei proste usytuowane podobnie, jak na tych rysunkach, a ostatnia prosta zawsze „sama wyjdzie”. Proszę spróbować!
Uzasadnienie jednak, że zadanie Pascala ma rozwiązanie, w matematyce jest
równoważne temu, że...
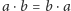 – i kto by to pomyślał! Nie jest
jednak łatwo się o tym przekonać.
– i kto by to pomyślał! Nie jest
jednak łatwo się o tym przekonać.
* * *
Ćwierć tysiąclecia później Gino FANO, jeden z członków słynnej Włoskiej
Szkoły Matematycznej, na wzór której po pierwszej wojnie światowej powstała
Polska Szkoła Matematyczna, udowodnił, że siedmiu drzew nie da się
posadzić w siedmiu rzędach, po trzy w każdym rzędzie, bo gdyby się dało, to
dałoby się również sprawdzić, że
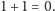 To już wymaga wyższej
szkoły jazdy.
To już wymaga wyższej
szkoły jazdy.
* * *
No, a co z ósemką? To zadanie dla Ciebie, Czytelniku.
James Joseph SYLVESTER, Anglik, najpierw kabareciarz, potem matematyk, Ojciec Założyciel matematyki amerykańskiej (wykładał tam przed i po wojnie secesyjnej), patrząc na rysunki Desarguesa i Pascala, zauważył, że są na nich (nienarysowane) rzędy, w których są tylko dwa drzewa. Postawił więc pytanie:
A czy istnieje sad, w którym nie wszystkie drzewa stoją w jednym rzędzie, ale w każdym rzędzie są co najmniej 3 drzewa?
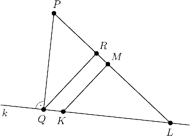
Rys. 3
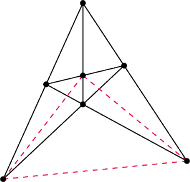
Rys. 4
I choć odpowiedź wydawała się oczywista – nie (oczywiście rozpatrujemy tylko sady ze skończoną liczbą drzew), to ładny dowód został podany dopiero 60 lat temu. Przedstawił go Theodore MOTZKIN. Oto ten
Dowód. Przypuśćmy, że jest sad mający skończoną liczbę drzew,
które nie wszystkie stoją w jednym rzędzie, ale na każdej prostej
wyznaczonej przez dwa drzewa rośnie jeszcze co najmniej jedno drzewo.
Dla
każdego drzewa wybierzmy ten rząd drzew, do którego ono nie należy,
ale do którego ma najbliżej (jeśli jest takich kilka, to wybierzmy
któryś z nich). Teraz wśród wybranych par
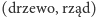 wybierzmy tę, dla której odległość ta jest najmniejsza. Niech parą tą
będzie
wybierzmy tę, dla której odległość ta jest najmniejsza. Niech parą tą
będzie
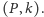 Oznaczmy przez
Oznaczmy przez
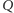 rzut
rzut
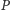 na
na
 Zgodnie z naszym przypuszczeniem na
Zgodnie z naszym przypuszczeniem na
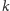 są co najmniej trzy
punkty, zatem co najmniej dwa z nich leżą po jednej stronie punktu
są co najmniej trzy
punkty, zatem co najmniej dwa z nich leżą po jednej stronie punktu
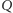 (zakładamy, że każda ze stron zaczyna się od punktu
(zakładamy, że każda ze stron zaczyna się od punktu
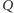 )
– oznaczmy je kolejno
)
– oznaczmy je kolejno
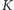 i
i
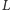 (rysunek 3). Wtedy wysokość
(rysunek 3). Wtedy wysokość
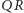 w trójkącie prostokątnym
w trójkącie prostokątnym
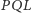 jest krótsza
od
jest krótsza
od
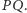 Na dodatek
Na dodatek
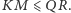 Zatem odległość punktu
Zatem odległość punktu
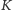 od prostej
od prostej
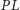 jest mniejsza od odległości
jest mniejsza od odległości
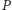 od
od
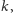 która miała być najmniejsza – otrzymana sprzeczność
kończy dowód.
która miała być najmniejsza – otrzymana sprzeczność
kończy dowód.
Powstało więc pytanie, ile co najmniej jest takich „dwudrzewnych” rzędów
w sadzie złożonym z
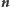 drzew. Motzkin udowodnił (1951), że więcej
niż
drzew. Motzkin udowodnił (1951), że więcej
niż
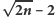 , L.M. Kelly i W.O.J. Moser wykazali (1958), że jest ich
co najmniej
, L.M. Kelly i W.O.J. Moser wykazali (1958), że jest ich
co najmniej
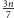 i że tego już poprawić się nie da, co widać
na rysunku 4.
i że tego już poprawić się nie da, co widać
na rysunku 4.
* * *
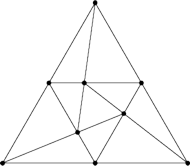
Rys. 5
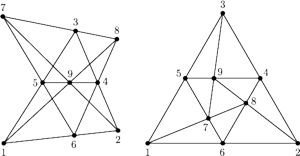
Rys. 6
Problem Pascala można rozwiązać też w inny sposób (Rys. 5). Ale jak się przekonać, że ten sposób jest inny? Ponumerujmy punkty w obu obrazkach ilustrujących problem dziewięciu drzew (Rys. 6).
Jeżeli ustalimy na każdym z nich punkty 1, 2, 3, 4, 5, 6, to na obrazku z lewej możemy punkt 7 dobrać prawie dowolnie na prostej 56 i dokończyć rysunek. Natomiast na obrazku z prawej poruszenie punktu 7 nie pozwoli rysunku dokończyć. Zatem rysunki te są rzeczywiście różne, a nie tylko inaczej narysowane.
W geometriach dyskretnych wielokąt
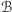 nazywamy wpisanym
w wielokąt
nazywamy wpisanym
w wielokąt
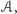 jeśli ma on wierzchołki na prostych zawierających boki
wielokąta
jeśli ma on wierzchołki na prostych zawierających boki
wielokąta
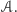
Na obu rysunkach trójkąt 123 jest wpisany w trójkąt 789, ten z kolei jest wpisany w trójkąt 456, a ten – o dziwo – w trójkąt 123.
No, a czy można znaleźć takie trójkąty
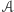 i
i
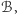 by
by
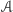 był wpisany w
był wpisany w
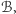 a
a
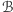 w
w
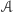 ?
?
Okazuje się, że nie.