Twierdzenie z happy endem
Zdarza się czasem, że zachód słońca i pusta, piaszczysta plaża zachwycają nas, kiedy patrzymy na nie, spacerując brzegiem morza, jednak zamknięte w martwe ramy zdjęcia przywodzą na myśl co najwyżej słowo „kicz”. Ta historia, gdyby jeden z hollyłódzkich reżyserów zdecydował się nakręcić film na jej podstawie, wydałaby się z pewnością banalna. Tymczasem napisało ją życie.
Napisało i umieściło w niesamowitym, matematycznym świecie, przez co nabrała szczególnego uroku. Posłuchajcie opowieści o niezwykłej więzi, jaka połączyła dwoje ludzi... A może będzie to opowieść o tym, jak niezwykła więź połączyła dwoje ludzi z matematyką? Przeczytajcie i oceńcie sami.
Lata trzydzieste ubiegłego stulecia były, z wielu względów, dla mieszkańców Węgier czasem trudnym. Ale zima w roku 1933 była wyjątkowo piękna. Oprószony śniegiem urokliwy Park Miejski czy pełne czaru kawiarenki w Budapeszcie stanowiły idealne miejsce spotkań. Grupka młodych ludzi (między innymi Paul Erdős, Paul Turán, George Szekeres i Esther Klein) tę zimową scenerię uznała za idealne tło dla długich i inspirujących rozmów o... matematyce. Któregoś mroźnego, niedzielnego popołudnia Esther, która wyjątkową miłością pałała do problemów geometrycznych, podzieliła się z kolegami pewną obserwacją.
Twierdzenie (Esther Klein, 1933). Wśród dowolnych pięciu punktów na płaszczyźnie, z których żadne trzy nie leżą na jednej prostej, zawsze znajdziemy cztery punkty które są wierzchołkami wypukłego czworokąta.
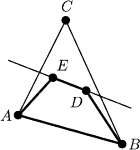
Rys. 1
Dowód. Wystarczy przeanalizować
trzy rodzaje możliwych konfiguracji pięciu punktów na płaszczyźnie.
Jeżeli leżą one w wierzchołkach pięciokąta wypukłego, to dowolne cztery
z nich spełniają tezę twierdzenia. Zachodzi ona również, gdy cztery
punkty tworzą wypukły czworokąt, a piąty punkt leży w jego wnętrzu
lub na zewnątrz. Pozostaje do sprawdzenia „najgorszy” przypadek, gdy
trzy punkty
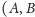 i
i
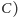 są wierzchołkami trójkąta, wewnątrz
którego leżą dwa pozostałe
są wierzchołkami trójkąta, wewnątrz
którego leżą dwa pozostałe
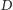 i
i
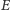 (Rys. 1). Wówczas
prosta przechodząca przez wewnętrzne punkty
(Rys. 1). Wówczas
prosta przechodząca przez wewnętrzne punkty
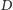 i
i
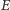 musi przeciąć dokładnie dwa boki trójkąta, gdyż
zgodnie z założeniem o niewspółliniowości żaden z wierzchołków
nie może na niej leżeć. Ale w takim przypadku wierzchołki
musi przeciąć dokładnie dwa boki trójkąta, gdyż
zgodnie z założeniem o niewspółliniowości żaden z wierzchołków
nie może na niej leżeć. Ale w takim przypadku wierzchołki
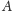 i
i
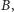 które leżą po jednej stronie prostej, wraz z punktami
które leżą po jednej stronie prostej, wraz z punktami
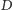 i
i
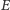 tworzą wypukły czworokąt
tworzą wypukły czworokąt
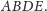
Ta niewinnie wyglądająca obserwacja geometryczna stała się dla Erdősa
i Szekeresa inspiracją do dalszych badań nad ciekawymi problemami
z pogranicza geometrii i kombinatoryki. Postawili nasuwające się od razu
pytanie: czy twierdzenie Esther Klein o czworokącie można uogólnić na
dowolne
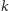 -kąty wypukłe? Innymi słowy, czy w odpowiednio dużym
i „porządnym” zbiorze punktów na płaszczyźnie można zawsze odnaleźć
wielokąt wypukły o zadanej liczbie wierzchołków? Wkrótce opublikowali oni
wspólną pracę, która stała się motorem szybkiego rozwoju geometrii
kombinatorycznej. Ich główne twierdzenie dawało pozytywną odpowiedź na
postawione wcześniej pytanie.
-kąty wypukłe? Innymi słowy, czy w odpowiednio dużym
i „porządnym” zbiorze punktów na płaszczyźnie można zawsze odnaleźć
wielokąt wypukły o zadanej liczbie wierzchołków? Wkrótce opublikowali oni
wspólną pracę, która stała się motorem szybkiego rozwoju geometrii
kombinatorycznej. Ich główne twierdzenie dawało pozytywną odpowiedź na
postawione wcześniej pytanie.
Twierdzenie (Erdős, Szekeres, 1935). Dla każdej liczby
naturalnej
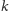 istnieje taka liczba naturalna
istnieje taka liczba naturalna
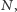 że wśród
dowolnych
że wśród
dowolnych
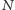 punktów na płaszczyźnie, z których żadne trzy
nie leżą na jednej prostej, zawsze znajdziemy
punktów na płaszczyźnie, z których żadne trzy
nie leżą na jednej prostej, zawsze znajdziemy
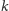 punktów, które są
wierzchołkami wypukłego
punktów, które są
wierzchołkami wypukłego
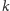 -kąta.
-kąta.
W dowodzie autorzy wykorzystali twierdzenie Ramseya (należy ono
obecnie do klasyki kombinatoryki) oraz wcześniejszą obserwację Esther Klein.
Jasne jest, że jeżeli znajdziemy jakąkolwiek liczbę
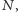 która spełnia tezę
powyższego twierdzenia, to każda liczba większa od niej też ją musi spełniać.
Naturalny staje się problem wyznaczenia najmniejszej takiej liczby dla
zadanego
która spełnia tezę
powyższego twierdzenia, to każda liczba większa od niej też ją musi spełniać.
Naturalny staje się problem wyznaczenia najmniejszej takiej liczby dla
zadanego
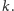 Oznaczmy ją (tak jak w oryginalnej pracy) przez
Oznaczmy ją (tak jak w oryginalnej pracy) przez
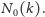 Spróbujmy wyznaczyć wartości
Spróbujmy wyznaczyć wartości
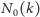 dla kilku
początkowych
dla kilku
początkowych
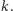 Trywialnie
Trywialnie
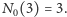

Rys. 2 Osiem punktów bez wypukłego pięciokąta
Twierdzenie Esther Klein, połączone z obserwacją, że nie każdy czworokąt
na płaszczyźnie jest wypukły, daje nam
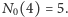 Wykazanie, że
Wykazanie, że
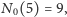 wymaga nieco więcej zachodu. Rysunek 2 przedstawia układ
ośmiu punktów, z których żadne trzy nie leżą na jednej prostej i żadne
pięć nie tworzy wypukłego pięciokąta. Dowód, że wśród dziewięciu
punktów sytuacja taka nie może zaistnieć, jest znacznie trudniejszy i po raz
pierwszy znalazł go Makai (ten dowód nie został nigdzie opublikowany,
ale był cytowany przez Erdősa i Szekeresa). Czy znając pierwsze trzy
wartości ciągu
wymaga nieco więcej zachodu. Rysunek 2 przedstawia układ
ośmiu punktów, z których żadne trzy nie leżą na jednej prostej i żadne
pięć nie tworzy wypukłego pięciokąta. Dowód, że wśród dziewięciu
punktów sytuacja taka nie może zaistnieć, jest znacznie trudniejszy i po raz
pierwszy znalazł go Makai (ten dowód nie został nigdzie opublikowany,
ale był cytowany przez Erdősa i Szekeresa). Czy znając pierwsze trzy
wartości ciągu
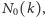 można dostrzec jakąś prawidłowość?
można dostrzec jakąś prawidłowość?
Erdős i Szekeres zauważyli, że

i, mimo że nie znali wartości
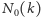 dla żadnego większego
dla żadnego większego
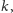 a oszacowania, które wynikały z dowodu ich twierdzenia, wyglądały
na istotnie nadmiarowe, to pokusili się o postawienie bardzo śmiałej hipotezy,
mówiącej, że dla dowolnego
a oszacowania, które wynikały z dowodu ich twierdzenia, wyglądały
na istotnie nadmiarowe, to pokusili się o postawienie bardzo śmiałej hipotezy,
mówiącej, że dla dowolnego
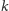

Dopiero w roku 1961 opublikowali oni pracę, w której pokazali (przez jawną
konstrukcję), że
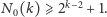 Niestety, wyznaczenie dokładnych
wartości
Niestety, wyznaczenie dokładnych
wartości
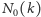 okazało się zagadnieniem o wiele bardziej złożonym.
Do dnia dzisiejszego pokazano jedynie, że
okazało się zagadnieniem o wiele bardziej złożonym.
Do dnia dzisiejszego pokazano jedynie, że
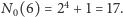 Dokonali
tego Szekeres i Peters wspomagani przez program komputerowy, który
pomógł przeanalizować różne położenia 17 punktów na płaszczyźnie
i stwierdzić, że w każdym z nich pojawił się wypukły sześciokąt.
Wkład ludzki polegał w tym przypadku na znacznym ograniczeniu zbioru
konfiguracji, które wymagały analizy komputerowej. Wynik ten ukazał się
drukiem dopiero w 2006 roku, a więc rok po śmierci Szekeresa. Wydaje się
niemożliwe, aby metoda komputerowa mogła pomóc przy wyznaczaniu
Dokonali
tego Szekeres i Peters wspomagani przez program komputerowy, który
pomógł przeanalizować różne położenia 17 punktów na płaszczyźnie
i stwierdzić, że w każdym z nich pojawił się wypukły sześciokąt.
Wkład ludzki polegał w tym przypadku na znacznym ograniczeniu zbioru
konfiguracji, które wymagały analizy komputerowej. Wynik ten ukazał się
drukiem dopiero w 2006 roku, a więc rok po śmierci Szekeresa. Wydaje się
niemożliwe, aby metoda komputerowa mogła pomóc przy wyznaczaniu
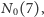
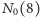 i kolejnych wartości. Najlepsze, jak do tej pory,
górne oszacowanie na
i kolejnych wartości. Najlepsze, jak do tej pory,
górne oszacowanie na
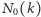 znaleźli w 2005 roku Tóth i Valtr,
dowodząc, że
znaleźli w 2005 roku Tóth i Valtr,
dowodząc, że

Jak widać, jest ono bardzo dalekie od tego, które 70 lat wcześniej przedstawili Erdős i Szekeres.
Tutaj historia tego twierdzenia wcale nie musi się skończyć. Być może to właśnie Ty, Czytelniku, będziesz autorem scenariusza do kolejnej części. Ale teraz pewnie zastanawiasz się, gdzie jest obiecywany happy end. Otóż wspomniana na samym początku obserwacja geometryczna Esther Klein nie tylko zainspirowała George’a Szekeresa do zajęcia się problemem w ujęciu matematycznym, ale też skierowała jego uwagę na osobę autorki. Zaledwie w rok po opublikowaniu artykułu Erdősa i Szekeresa odbył się ślub George’a i Esther. Twierdzenie Esther Klein zyskało nazwę twierdzenia z happy endem, a państwo Szekeres żyli długo i szczęśliwie.
THE END