Stowarzyszenie na rzecz Edukacji Matematycznej
O publikacji „Matematyka. Poszukuję – odkrywam”
W grudniu 2010 roku ukazał się drugi tom serii wydawniczej Biblioteczka Stowarzyszenia na rzecz Edukacji Matematycznej zatytułowany Matematyka. Poszukuję – odkrywam. Materiały w nim zawarte stanowią opracowania referatów wygłoszonych w ramach konferencji Konkursy matematyczne w Polsce, zorganizowanej w 2008 roku przez Uniwersytet Warszawski we współpracy ze Stowarzyszeniem na rzecz Edukacji Matematycznej.
Ze zbioru Matematyka. Poszukuję – odkrywam dowiemy się między innymi:
- w jaki sposób dobra znajomość wzorów skróconego mnożenia oraz technik ich stosowania może pomóc w rozwiązywaniu zadań olimpijskich,
- jak grać, żeby wygrać, czyli jak rozstrzygnąć, czy dla opisanej w zadaniu gry któryś z graczy ma strategię wygrywającą,
- jak sobie radzić z dowodzeniem nierówności, gdy domyślamy się idei rozwiązania, ale problemy nastręcza ustalenie szczegółów,
- z jakich faktów warto korzystać, wykazując, że zadane cztery punkty leżą na jednym okręgu.
W publikacji znajdziemy ponadto pierwszy plakat wydany przez Stowarzyszenie na rzecz Edukacji Matematycznej Równe sumy pól wraz z omówieniem zawierającym dowody przedstawionych na nim zależności, a także ciekawe uogólnienie twierdzenia Ptolemeusza, którego najprostszą wersję przytaczam poniżej, zachęcając jednocześnie Czytelników do zapoznania się ze szczegółami zawartymi w broszurze.
Twierdzenie Ptolemeusza głosi:
Twierdzenie (Ptolemeusza). W czworokącie wypukłym wpisanym w okrąg iloczyn długości przekątnych jest równy sumie iloczynów długości przeciwległych boków.
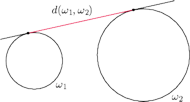
Rys. 1
Zdefiniujmy odległość styczną
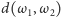 pary okręgów jako
odległość punktów styczności tych okregów do ich wspólnej stycznej
zewnętrznej (Rys. 1).
pary okręgów jako
odległość punktów styczności tych okregów do ich wspólnej stycznej
zewnętrznej (Rys. 1).
Rozważmy okręgi
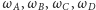 wszystkie styczne wewnętrznie (lub
wszystkie styczne zewnętrznie) do okręgu
wszystkie styczne wewnętrznie (lub
wszystkie styczne zewnętrznie) do okręgu
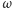 w wierzchołkach czworokąta
wypukłego
w wierzchołkach czworokąta
wypukłego
 (Rys. 2).
(Rys. 2).
Spełniona jest wówczas następująca równość:

Zauważmy, że twierdzenie Ptolemeusza jest rzeczywiście jej szczególnym
przypadkiem, który zachodzi, gdy okręgi
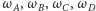 są punktami,
czyli okręgami zdegenerowanymi.
są punktami,
czyli okręgami zdegenerowanymi.
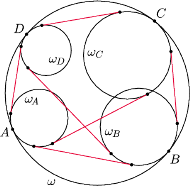
Rys. 2
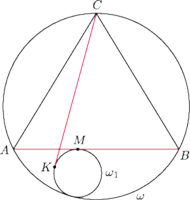
Rys. 3
Powyższe twierdzenie, zwane twierdzeniem Caseya, pozwala w wielu przypadkach podać bardzo krótkie dowody użytecznych faktów. Zobaczmy, jak możemy je wykorzystać do rozwiązania następującego zadania:
Zadanie. W koło o okręgu
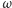 wpisano trójkąt równoramienny
wpisano trójkąt równoramienny
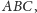 w którym
w którym
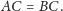 W odcinek koła wyznaczony
przez cięciwę
W odcinek koła wyznaczony
przez cięciwę
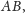 do którego nie należy punkt
do którego nie należy punkt
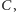 wpisano
okrąg
wpisano
okrąg
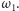 Z punktu
Z punktu
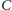 poprowadzono prostą styczną do okręgu
poprowadzono prostą styczną do okręgu
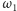 w punkcie
w punkcie
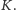 Wykaż, że długość odcinka
Wykaż, że długość odcinka
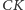 nie zależy od wyboru okręgu
nie zależy od wyboru okręgu
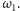
Oznaczmy przez
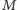 punkt styczności okręgu
punkt styczności okręgu
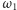 z prostą
z prostą
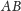 (Rys. 3).
(Rys. 3).
Zastosujmy twierdzenie Caseya do okręgów zdegenerowanych
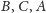 i okręgu
i okręgu
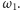 Korzystając z tego, że
Korzystając z tego, że
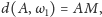
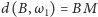 oraz
oraz
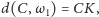 otrzymujemy
równość
otrzymujemy
równość
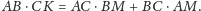 Stąd
Stąd
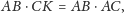 czyli
czyli
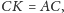 co kończy rozwiązanie zadania.
co kończy rozwiązanie zadania.
Więcej o broszurze Matematyka. Poszukuję – odkrywam można przeczytać na stronie internetowej www.omg.edu.pl.