Drobiazgi
O prostej Simsona raz jeszcze
Myślę, że niemal każdy Czytelnik miał okazję się z nią spotkać. Załóżmy,
że mamy dany trójkąt, i wybierzmy dowolny punkt
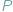 z okręgu na
nim opisanego. Wówczas rzuty prostokątne punktu
z okręgu na
nim opisanego. Wówczas rzuty prostokątne punktu
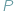 na proste
zawierające boki danego trójkąta leżą na jednej prostej zwanej prostą
Simsona.
na proste
zawierające boki danego trójkąta leżą na jednej prostej zwanej prostą
Simsona.
Rys. 1 Jedna z bardziej egzotycznych konfiguracji.
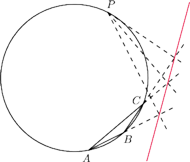
Rys. 2
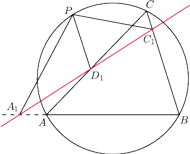
Rys. 3
Chyba najbardziej typowym dowodem tego faktu jest rachunek na kątach. Jednakże rozumowanie to ma pewną wadę: istnieje wiele możliwych konfiguracji (np. ta na rysunku 1, dość egzotyczna) i, aby je objąć jednym rachunkiem, trzeba uciec się do kątów skierowanych, co bywa nieczytelne dla osób niewprawionych w tego typu rozumowaniach. Istnieje jednak bardzo sprytny, krótki i przejrzysty dowód tego faktu, niewymagający ani kątów czy odcinków skierowanych, ani pracochłonnego rozważania wielu konfiguracji – oto on.
Dowód. Przyjmijmy, że punkt
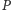 leży na łuku
leży na łuku
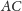 niezawierającym punktu
niezawierającym punktu
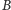 okręgu opisanego na danym
trójkącie
okręgu opisanego na danym
trójkącie
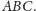 Jeśli
Jeśli
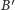 jest punktem leżącym na prostej
jest punktem leżącym na prostej
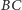 po przeciwnej stronie punktu
po przeciwnej stronie punktu
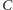 niż punkt
niż punkt
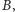 to
zachodzi równość
to
zachodzi równość
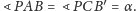 Niech
Niech
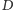 będzie
takim punktem na prostej
będzie
takim punktem na prostej
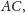 że
że
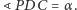 Oznaczając
odpowiednio przez
Oznaczając
odpowiednio przez
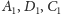 rzuty prostokątne punktu
rzuty prostokątne punktu
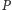 na
proste
na
proste
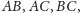 stwierdzamy, że
trójkąty prostokątne
stwierdzamy, że
trójkąty prostokątne
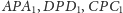 są podobne (Rys. 2). Mają
więc taki sam kąt przy wierzchołku
są podobne (Rys. 2). Mają
więc taki sam kąt przy wierzchołku
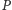 równy
równy
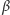 i stosunek
przyprostokątnej przy wierzchołku
i stosunek
przyprostokątnej przy wierzchołku
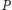 do przeciwprostokątnej
równy
do przeciwprostokątnej
równy
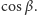 Rozważmy przekształcenie
będące złożeniem obrotu względem
Rozważmy przekształcenie
będące złożeniem obrotu względem
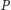 o kąt
o kąt
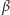 (w kierunku
od przeciwprostokątnej do przyprostokątnej) z jednokładnością o skali
(w kierunku
od przeciwprostokątnej do przyprostokątnej) z jednokładnością o skali
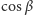 i środku w tym samym punkcie. Przekształcenie to jest
podobieństwem, więc w szczególności obrazem każdej prostej jest
prosta. Skoro punkty
i środku w tym samym punkcie. Przekształcenie to jest
podobieństwem, więc w szczególności obrazem każdej prostej jest
prosta. Skoro punkty
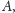
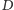 i
i
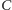 są współliniowe, to ich
obrazy
są współliniowe, to ich
obrazy
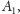
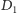 i
i
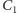 również, co kończy dowód.
również, co kończy dowód.
Czytelnik Wnikliwy bez trudu zauważy, że jeśli zamiast rzutów
prostokątnych weźmiemy „rzuty pod kątem
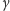 ” (wszystkie kąty tak samo
zorientowane, zobacz rysunek 3), to one również będą leżały na jednej prostej
i powyższy dowód bez trudu przenosi się na uogólnione zadanie.
” (wszystkie kąty tak samo
zorientowane, zobacz rysunek 3), to one również będą leżały na jednej prostej
i powyższy dowód bez trudu przenosi się na uogólnione zadanie.