Stowarzyszenie na rzecz Edukacji Matematycznej
LXII Olimpiada Matematyczna
13 i 14 kwietnia odbyły się zawody finałowe LXII OLimpiady Matematycznej. Każdego dnia zawodów 139 uczniów z całej Polski, przez trzysta minut, rozwiązywało trzy zadania. Wszystkie bezbłędnie rozwiązał Filip Borowiec z Kielc, a Maciej Dulęba z Wrocławia i Damian Orlef z Zabrza rozwiązali po pięć i pół.
Tym razem 126 finalistów rozwiązało przynajmniej jedno zadanie. Każdy z laureatów rozwiązał co najmniej trzy i pół zadania, a wyróżnieni po trzy. Finał był więc na pewno łatwiejszy niż przed rokiem.
Z zadaniami finału oraz szkicami ich rozwiązań można zapoznać się na stronie olimpiady pod adresem: www.om.edu.pl.
Niektórzy finaliści rozwiązali zadania bardzo elegancko w sposób nieprzewidziany przez osoby przygotowujące zadania. Omówimy dwa rozwiązania zadania drugiego. Różnią się one jedynie dowodem lematu.
Dowód lematu wg Wojciecha Nadary (nagroda im. A. Mąkowskiego).
Potęga punktu
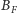 względem okręgu
względem okręgu
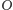 jest równa
jest równa
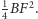 Tyle samo
jest równa potęga punktu
Tyle samo
jest równa potęga punktu
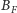 względem okręgu o środku
względem okręgu o środku
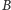 i promieniu
i promieniu
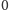 (czyli zdegenerowanego do punktu
(czyli zdegenerowanego do punktu
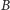 ). Analogicznie potęga
punktu
). Analogicznie potęga
punktu
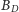 względem okręgu
względem okręgu
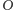 jest równa potędze punktu
jest równa potędze punktu
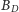 względem okręgu zdegenerowanego do punktu
względem okręgu zdegenerowanego do punktu
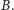 Wobec
tego jeśli punkt
Wobec
tego jeśli punkt
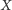 leży prostej
leży prostej
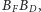 to jego potęgi względem
tych dwóch okręgów są równe (więc jest to ich oś potęgowa). Podobnie
prosta
to jego potęgi względem
tych dwóch okręgów są równe (więc jest to ich oś potęgowa). Podobnie
prosta
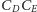 jest osią potęgową okręgu
jest osią potęgową okręgu
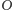 i okręgu zdegenerowanego
do punktu
i okręgu zdegenerowanego
do punktu
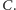 Wobec tego potęgi punktu
Wobec tego potęgi punktu
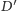 względem każdego
z okręgów zdegenerowanych do punktów
względem każdego
z okręgów zdegenerowanych do punktów
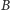 i
i
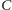 są równe
(bo równe jego potędze względem okręgu
są równe
(bo równe jego potędze względem okręgu
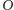 ). Oznacza to, że
). Oznacza to, że
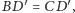 a to
teza lematu.
a to
teza lematu.
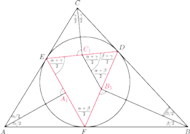
Dowód lematu wg Anny Olech. Niech
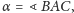
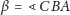 i
i
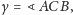
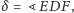
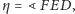
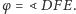 Wtedy
Wtedy
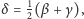
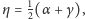
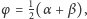 więc trójkąt
więc trójkąt
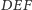 jest ostrokątny.
jest ostrokątny.
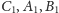 będą środkami odcinków
będą środkami odcinków
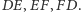 Na czworokącie
Na czworokącie
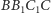 można opisać okrąg, bo
można opisać okrąg, bo
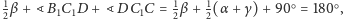 oczywiście
oczywiście
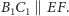 Proste
Proste
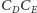 i
i
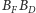 są symetralnymi odcinków
są symetralnymi odcinków
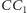 i
i
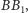 więc ich punkt przecięcia czyli
więc ich punkt przecięcia czyli
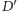 jest środkiem
okręgu opisanego na czworokącie
jest środkiem
okręgu opisanego na czworokącie
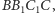 więc
więc
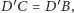 a to
chcieliśmy udowodnić.
a to
chcieliśmy udowodnić.