Sztuka anamorficzna

wikipedia
Ambasodorowie, Hans Holbein Młodszy (1498–1543)
Obrazem anamorficznym nazywamy obraz powstały przez celowe zniekształcenie jego proporcji w taki sposób, aby jego poprawny odczyt był możliwy przez popatrzenie na niego z ustalonej perspektywy lub odbicie go w odpowiednim zwierciadle.
Takie specjalne lustro nazywane jest anamorfoskopem i może nim być np. lustrzany cylinder, lustrzany stożek czy też zwyczajna łyżka. Dziedzina, która zajmuje się tworzeniem takich obrazów, nazywa się sztuką anamorficzną. Termin ten powszechnie nie jest znany, lecz to, co się kryje pod jego nazwą, obserwujemy praktycznie na co dzień. Współczesne anamorfozy są często atrakcjami turystycznymi, ale mają też charakter ozdobny, a przede wszystkim praktyczny.
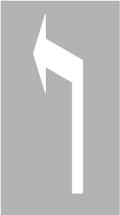
Rys. 1
Obrazy anamorficzne można zobaczyć w wielu miejscach. Aby się o tym przekonać, wystarczy przyjrzeć się chociażby poziomym znakom drogowym namalowanym na ulicach. Nietrudno zauważyć, że większość z nich jest nieproporcjonalnie rozciągnięta lub pogrubiona. Zabieg ten jest celowo stosowany przez projektantów, aby kierowcy jadący samochodem widzieli znaki we właściwych proporcjach. Obok przedstawiony został znak P-8c, czyli strzałka kierunkowa do skrętu w lewo.
W wielu miastach na świecie, np. Paryżu, Berlinie, Dun Laoghaire, można podziwiać wykorzystujące anamorfozę niesamowite malowidła na chodnikach, budynkach. Budzą one ogromne zainteresowanie wśród przechodniów.
Właściwości obrazu anamorficznego wykorzystywane są także w kinematografii, przy kręceniu filmów panoramicznych oraz nagrywaniu DVD. Podczas filmowania używane są kamery ze specjalnym anamorficznym obiektywem, który powoduje poziome „ściśnięcie” obrazu (około dwukrotne), a następnie w kinie do projektora zakładana jest odpowiednia anamorficzna soczewka, która rozciąga wyświetlany obraz. Dzięki takiej metodzie wykorzystywana jest cała dostępna powierzchnia taśmy filmowej, a w konsekwencji zapewniona jest największa możliwa rozdzielczość.
Pomysł ten przeniesiony został również na DVD z pewną różnicą – tutaj
rolę obiektywu anamorficznego pełni elektronika odtwarzacza DVD. W tym
przypadku rejestrowany obraz jest kompresowany do proporcji
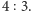 Jeśli
odbiornik telewizyjny wyposażony jest w odpowiednią opcję, obraz jest
dekompresowany i transformowany do formatu
Jeśli
odbiornik telewizyjny wyposażony jest w odpowiednią opcję, obraz jest
dekompresowany i transformowany do formatu
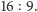 W przeciwnym
przypadku następuje redukcja liczby linii obrazu poprzez zmniejszenie
jego wysokości oraz dodanie u góry i z dołu czarnych pasów na
wyświetlanym obrazie.
W przeciwnym
przypadku następuje redukcja liczby linii obrazu poprzez zmniejszenie
jego wysokości oraz dodanie u góry i z dołu czarnych pasów na
wyświetlanym obrazie.
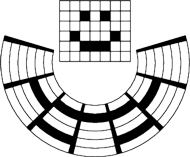
Rys. 2 Przykładowa siatka dla lustrzanego cylindra.
W malarstwie najbardziej znanym przykładem zastosowania anamorfozy jest
dzieło namalowane w XVI wieku przez Hansa Holbeina Młodszego, noszące
tytuł Ambasadorowie. Poza przedstawionymi postaciami oraz licznymi detalami
o bogatej symbolice uwagę skupia podłużny, ukośny kształt w dolnej części
obrazu. Z pozoru nic nieprzypominająca smuga okazuje się ludzką czaszką. Aby
się o tym przekonać, wystarczy punkt obserwacji umieścić nad obrazem
(pod kątem ok.
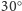 ) na drodze wiodącej w kierunku wyznaczonym przez
tę deformację. Co ciekawe, Czytelnik może spróbować zobaczyć czaszkę na
uwypukleniu łyżki.
) na drodze wiodącej w kierunku wyznaczonym przez
tę deformację. Co ciekawe, Czytelnik może spróbować zobaczyć czaszkę na
uwypukleniu łyżki.
Metoda, przy użyciu której wykonuje się tego rodzaju obrazy anamorficzne, jest, oczywiście, zwykłym rzutowaniem perspektywicznym, w związku z czym do poprawnego odczytania nie trzeba dysponować żadnym specjalnym zwierciadłem.
Sytuacja jednak znacznie się komplikuje, gdy obraz anamorficzny chcemy uzyskać przez odbicie w lustrzanym cylindrze. Na przestrzeni wieków ludzie próbowali w różny sposób radzić sobie z tym problemem. Za każdym razem myślą przewodnią było stworzenie odpowiedniej siatki kołowej (Rys. 2).
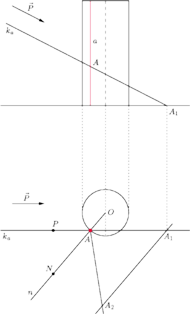
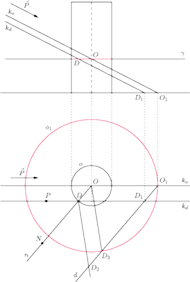
Rys. 3 Schemat odbicia tworzącej walca, górna część: rzut z boku, dolna: rzut z góry.
Idea ta polegała na tym, aby najpierw podzielić dany obraz w szachownicę, a następnie w pewien intuicyjny sposób narysować obraz anamorficzny zawartości oczek takiej siatki. Dzięki takiemu zabiegowi problem redukował się do malowania oddzielnie małych fragmentów anamorficznych w każdym polu. Przez długi czas nie umiano jednak wyznaczyć dokładnego obrazu anamorficznego wybranego punktu, a w konsekwencji również precyzyjnej siatki kołowej. Z czasem jednak udało się znaleźć rozwiązanie tego problemu.
Zakładamy, że obserwator (oko) jest dostatecznie daleko od lustrzanego
cylindra, a obraz anamorficzny jest wyznaczony przez promienie równoległe do
danego wektora
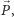 nie zaś przez jeden środek rzutów. Znalezienie
siatki kołowej sprowadza się do wyznaczenia obrazu anamorficznego dwóch
szczególnych krzywych leżących na walcu – tworzącej walca oraz okręgu
leżącego w jego przekroju poprzecznym. Najpierw znajdziemy obraz
tworzącej walca. Przyjmijmy oznaczenia takie jak na rysunku 3. Niech wektor
nie zaś przez jeden środek rzutów. Znalezienie
siatki kołowej sprowadza się do wyznaczenia obrazu anamorficznego dwóch
szczególnych krzywych leżących na walcu – tworzącej walca oraz okręgu
leżącego w jego przekroju poprzecznym. Najpierw znajdziemy obraz
tworzącej walca. Przyjmijmy oznaczenia takie jak na rysunku 3. Niech wektor
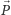 oznacza kierunek rzutowania, natomiast
oznacza kierunek rzutowania, natomiast
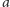 tworzącą walca.
Na początku wyznaczymy obraz dowolnego punktu
tworzącą walca.
Na początku wyznaczymy obraz dowolnego punktu
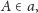 rozwiązując
przy okazji podstawowy problem, z którym dawniej nie mogli uporać się
malarze. W tym celu poprowadźmy prostą
rozwiązując
przy okazji podstawowy problem, z którym dawniej nie mogli uporać się
malarze. W tym celu poprowadźmy prostą
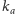 równoległą do kierunku
rzutowania, przechodzącą przez punkt
równoległą do kierunku
rzutowania, przechodzącą przez punkt
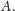 Korzystając z górnej
części rysunku 3, przedstawiającej rzut walca z boku, wyznaczamy punkt
Korzystając z górnej
części rysunku 3, przedstawiającej rzut walca z boku, wyznaczamy punkt
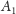 będący punktem przecięcia prostej
będący punktem przecięcia prostej
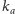 oraz płaszczyzny
rzutowania. Przez
oraz płaszczyzny
rzutowania. Przez
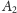 oznaczmy szukany obraz anamorficzny punktu
oznaczmy szukany obraz anamorficzny punktu
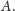
Rys. 4 Schemat odbicia okręgu leżącego w przekroju poprzecznym walca, górna część: rzut z boku, dolna: rzut z góry.
Spójrzmy teraz na dolną część rysunku 3 przedstawiającą rzut walca z góry.
Zauważmy, że w rzucie prostokątnym mamy równość odcinków
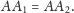 Oznaczmy teraz przez
Oznaczmy teraz przez
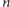 prostą prostopadłą do
powierzchni walca przechodzącą przez punkt
prostą prostopadłą do
powierzchni walca przechodzącą przez punkt
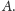 Zgodnie z prawem
fizycznym mówiącym, że kąt padania jest równy kątowi odbicia, mamy
równość kątów:
Zgodnie z prawem
fizycznym mówiącym, że kąt padania jest równy kątowi odbicia, mamy
równość kątów:
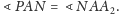 Ponadto z równości kątów
wierzchołkowych wynika, że
Ponadto z równości kątów
wierzchołkowych wynika, że
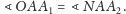 W związku z tym
również kąty przy podstawie trójkąta równoramiennego
W związku z tym
również kąty przy podstawie trójkąta równoramiennego
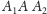 mają
tę samą miarę. Z tego z kolei wynika równoległość prostych
mają
tę samą miarę. Z tego z kolei wynika równoległość prostych
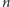 i
i
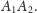 Obierając inny punkt na prostej
Obierając inny punkt na prostej
 – oznaczmy go
– oznaczmy go
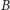 – i postępując analogicznie, otrzymamy punkty
– i postępując analogicznie, otrzymamy punkty
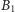 i
i
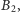 przy czym (wobec tego, że prosta
przy czym (wobec tego, że prosta
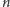 będzie ta sama) trójkąty
będzie ta sama) trójkąty
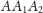 i
i
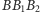 będą podobne. Zatem obrazem anamorficznym
tworzącej
będą podobne. Zatem obrazem anamorficznym
tworzącej
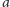 będzie półprosta
będzie półprosta
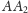 o wierzchołku w punkcie
o wierzchołku w punkcie
 Zastanówmy się teraz, jaki będzie obraz anamorficzny okręgu
Zastanówmy się teraz, jaki będzie obraz anamorficzny okręgu
 wyznaczonego przez przekrój walca płaszczyzną
wyznaczonego przez przekrój walca płaszczyzną
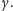 Przyjmijmy,
że promień walca jest równy
Przyjmijmy,
że promień walca jest równy
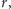 natomiast punkt
natomiast punkt
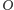 należy
jednocześnie do osi walca i płaszczyzny
należy
jednocześnie do osi walca i płaszczyzny
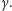 Wówczas
Wówczas
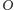 jest
środkiem okręgu
jest
środkiem okręgu
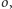 a
a
 jego promieniem. Niech
jego promieniem. Niech
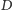 będzie
dowolnym punktem okręgu
będzie
dowolnym punktem okręgu
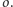 Poprowadźmy (Rys. 4) dwie proste
równoległe do kierunku rzutowania –
Poprowadźmy (Rys. 4) dwie proste
równoległe do kierunku rzutowania –
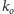 oraz
oraz
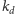 – przechodzące
odpowiednio przez punkty
– przechodzące
odpowiednio przez punkty
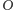 oraz
oraz
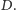 Oznaczmy przez
Oznaczmy przez
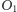 oraz
oraz
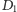 punkty przecięcia tych prostych z płaszczyzną
rzutowania, natomiast przez
punkty przecięcia tych prostych z płaszczyzną
rzutowania, natomiast przez
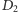 szukany obraz anamorficzny punktu
szukany obraz anamorficzny punktu
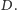 W obrazie rzutu prostopadłego zachodzi, oczywiście, równość
odcinków
W obrazie rzutu prostopadłego zachodzi, oczywiście, równość
odcinków
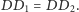 Dodatkowo, podobnie jak w poprzednim
przypadku, korzystając z prawa odbicia, otrzymujemy równość kątów
Dodatkowo, podobnie jak w poprzednim
przypadku, korzystając z prawa odbicia, otrzymujemy równość kątów
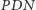 i
i
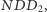 która pociąga za sobą następującą równość:
która pociąga za sobą następującą równość:

Zatem punkty
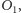
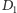 i
i
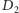 są współliniowe. Rozważmy
teraz okrąg o środku
są współliniowe. Rozważmy
teraz okrąg o środku
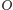 przechodzący przez
przechodzący przez
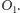 Oznaczmy przez
Oznaczmy przez
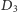 punkt przecięcia prostej
punkt przecięcia prostej
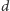 z okręgiem
z okręgiem
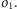 Wówczas
czworokąt
Wówczas
czworokąt
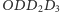 jest równoległobokiem o bokach równych co do
długości promieniom okręgów
jest równoległobokiem o bokach równych co do
długości promieniom okręgów
 oraz
oraz
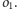 Z przeprowadzonej
analizy wynika, że obraz anamorficzny punktu
Z przeprowadzonej
analizy wynika, że obraz anamorficzny punktu
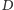 leży na prostej
przechodzącej przez punkty
leży na prostej
przechodzącej przez punkty
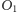 oraz
oraz
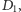 a ponadto znajduje się
w odległości
a ponadto znajduje się
w odległości
 od drugiego punktu przecięcia tej prostej z okręgiem
od drugiego punktu przecięcia tej prostej z okręgiem
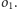 W celu wyznaczenia obrazu anamorficznego okręgu
W celu wyznaczenia obrazu anamorficznego okręgu
 wystarczy
zatem poprowadzić półproste z punktu
wystarczy
zatem poprowadzić półproste z punktu
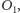 a następnie wyznaczyć
na nich punkty odległe o
a następnie wyznaczyć
na nich punkty odległe o
 od punktów ich przecięcia z okręgiem
od punktów ich przecięcia z okręgiem
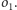 Krzywa, jaką otrzymamy w wyniku takiego procesu, nosi nazwę
ślimaka Pascala.
Krzywa, jaką otrzymamy w wyniku takiego procesu, nosi nazwę
ślimaka Pascala.
Jak się zatem okazuje, krzywa będąca obrazem anamorficznym okręgu leżącego w przekroju poprzecznym walca nie jest łatwa do określenia na pierwszy rzut oka. Nie ma się zatem co dziwić malarzom, którzy przez długi czas mieli problemy z wyznaczeniem dokładnej siatki kołowej. Z czasem udało się również zbudować urządzenie mechaniczne (przypominające swym wyglądem wielonogi cyrkiel) służące do wykreślania tego typu siatek, które jednak w dobie grafiki komputerowej chyba znacznie traci na wartości. W szczególności dostępne są darmowe programy generujące obrazy anamorficzne w przekształceniu walcowym dowolnego zdjęcia. Przykładem takiego programu jest Anamorph Me!. Wiele niezwykłych obrazów grafiki anamorficznej Czytelnik może znaleźć bez trudu w Internecie pod hasłem anamorphic art.
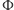 o biegunie
o biegunie
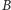 i promieniu
i promieniu
 to
zbiór punktów leżacych na dowolnej z prostych przechodzących przez
to
zbiór punktów leżacych na dowolnej z prostych przechodzących przez
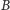 i odległych o
i odległych o
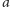 od jej przecięcia z
od jej przecięcia z
 Ślimak
Pascala to taka szczególna konchoida okręgu, której biegun leży na tym
okręgu.
Ślimak
Pascala to taka szczególna konchoida okręgu, której biegun leży na tym
okręgu.
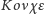 (konche) to po grecku muszla – stąd pochodzi nazwa
ślimaka Pascala. Jest on krzywą stopnia 4; jeśli okrąg o promieniu
(konche) to po grecku muszla – stąd pochodzi nazwa
ślimaka Pascala. Jest on krzywą stopnia 4; jeśli okrąg o promieniu
 umieścimy tak, by miał równanie
umieścimy tak, by miał równanie
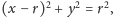 jego
konchoida o biegunie
jego
konchoida o biegunie
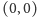 i promieniu
i promieniu
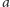 będzie miała
równanie
będzie miała
równanie
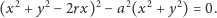
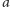 jest równe, odpowiednio,
jest równe, odpowiednio,
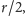
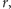
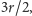
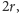
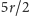 ; czwarta z nich ma
osobną nazwę – to kardioida.
; czwarta z nich ma
osobną nazwę – to kardioida.