Urok zbioru

Tematem mojej pracy były własności pewnych szczególnych punktów na
płaszczyźnie – punktów tytułowego zbioru
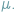 W poniższym tekście
przedstawię niektóre z tych własności oraz przykłady pokazujące, że przy
użyciu dowiedzionych twierdzeń można wyciągnąć wiele niemal
natychmiastowych wniosków.
W poniższym tekście
przedstawię niektóre z tych własności oraz przykłady pokazujące, że przy
użyciu dowiedzionych twierdzeń można wyciągnąć wiele niemal
natychmiastowych wniosków.
Definicja.
Niech
 będzie zbiorem punktów na płaszczyźnie.
Weźmy taki punkt
będzie zbiorem punktów na płaszczyźnie.
Weźmy taki punkt
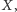 że dla każdej prostej
że dla każdej prostej
 przechodzącej
przez
przechodzącej
przez
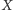 suma kwadratów odległości punktów
suma kwadratów odległości punktów
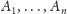 od
od
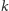 jest taka sama. Zbiór
jest taka sama. Zbiór
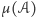 definiujemy jako zbiór
wszystkich punktów
definiujemy jako zbiór
wszystkich punktów
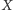 spełniających powyższy warunek.
spełniających powyższy warunek.
Na przykład, jest oczywiste, że dla dowolnego punktu
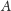 zachodzi
zachodzi
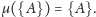 Natomiast pierwszy przypadek zbioru
Natomiast pierwszy przypadek zbioru
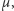 z którym
się zetknąłem, pochodzi z Olimpiady Matematycznej Gimnazjalistów. Poniżej
podaję rozwiązanie jednego z uczestników.
z którym
się zetknąłem, pochodzi z Olimpiady Matematycznej Gimnazjalistów. Poniżej
podaję rozwiązanie jednego z uczestników.

Weźmy dowolną prostą
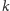 przechodzącą przez
przechodzącą przez
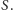 Poprowadźmy
do niej prostopadłą w
Poprowadźmy
do niej prostopadłą w
 i nazwijmy ją
i nazwijmy ją
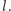 Przez
Przez
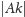 będziemy oznaczać odległość punktu
będziemy oznaczać odległość punktu
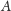 od prostej
od prostej
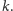 Z twierdzenia Pitagorasa wynika równość
Z twierdzenia Pitagorasa wynika równość
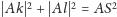 oraz analogiczne równości dla punktów
oraz analogiczne równości dla punktów
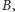

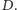 Wobec
tego sumy kwadratów odległości od
Wobec
tego sumy kwadratów odległości od
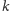 i
i
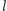 wzięte razem dają
wzięte razem dają
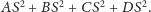 Ponadto, ze względu na symetrię sytuacji, sumy
odległości wierzchołków kwadratu od prostych
Ponadto, ze względu na symetrię sytuacji, sumy
odległości wierzchołków kwadratu od prostych
 i
i
 muszą być
równe. Zatem suma kwadratów odległości
muszą być
równe. Zatem suma kwadratów odległości
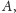
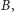
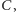
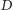 od
od
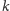 wynosi
wynosi
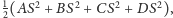 więc jest
niezależna od wyboru
więc jest
niezależna od wyboru
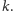
Inną metodą rozwiązania jest wykazanie najpierw, że
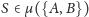 i analogicznie
i analogicznie
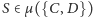 ; stąd już łatwo wynika teza. Można
wyobrazić sobie sporo przykładów opartych na podobnych obserwacjach.
Próba znalezienia ogólnych warunków na to, kiedy zbiór
; stąd już łatwo wynika teza. Można
wyobrazić sobie sporo przykładów opartych na podobnych obserwacjach.
Próba znalezienia ogólnych warunków na to, kiedy zbiór
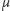 jest
niepusty, lub też kiedy dany punkt należy do zbioru
jest
niepusty, lub też kiedy dany punkt należy do zbioru
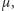 w naturalny
sposób prowadzi do poniższego twierdzenia. Podaje ono takie warunki
wyrażone analitycznie, a ponadto pozwala na wyciąganie dość ogólnych
wniosków, które zostaną zaprezentowane dalej.
w naturalny
sposób prowadzi do poniższego twierdzenia. Podaje ono takie warunki
wyrażone analitycznie, a ponadto pozwala na wyciąganie dość ogólnych
wniosków, które zostaną zaprezentowane dalej.
Twierdzenie. Niech
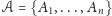 będzie zbiorem punktów na
płaszczyźnie, a
będzie zbiorem punktów na
płaszczyźnie, a
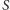 – środkiem masy tych punktów. Wówczas
zbiór
– środkiem masy tych punktów. Wówczas
zbiór
 jest jedno- lub dwuelementowy i symetryczny względem
jest jedno- lub dwuelementowy i symetryczny względem
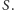
Dowód. Wprowadźmy układ współrzędnych zespolonych. Liczbę
zespoloną odpowiadającą punktowi
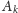 będziemy oznaczać
będziemy oznaczać
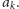 Sprawdźmy najpierw warunki równoważne temu, że
Sprawdźmy najpierw warunki równoważne temu, że
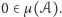 Zamiast obliczać odległości naszych punktów od zmiennej prostej
przechodzącej przez
Zamiast obliczać odległości naszych punktów od zmiennej prostej
przechodzącej przez
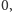 będziemy dla zmiennej liczby
będziemy dla zmiennej liczby
 z okręgu
jednostkowego liczyć odległości
z okręgu
jednostkowego liczyć odległości
 czyli obróconych wokół
czyli obróconych wokół
 punktów
punktów
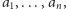 od prostej urojonej. Zgodnie ze wzorem
od prostej urojonej. Zgodnie ze wzorem
 suma kwadratów odległości tych punktów od prostej
urojonej to
suma kwadratów odległości tych punktów od prostej
urojonej to

Pierwszy człon jest stały, natomiast gdy
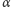 przebiega okrąg jednostkowy,
liczba w nawiasie przebiega okrąg o środku w
przebiega okrąg jednostkowy,
liczba w nawiasie przebiega okrąg o środku w
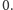 Gdy
Gdy
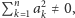 część rzeczywista, oczywiście, jest zmienna – dlatego
część rzeczywista, oczywiście, jest zmienna – dlatego
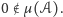 W
przeciwnym przypadku rozważany okrąg jest zdegenerowany do punktu i wtedy
W
przeciwnym przypadku rozważany okrąg jest zdegenerowany do punktu i wtedy
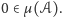
Otrzymaliśmy więc warunek konieczny i dostateczny dla zera. Aby
sprawdzić warunek dla punktu
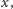 wystarczy przesunąć nasze punkty
o wektor
wystarczy przesunąć nasze punkty
o wektor
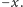 Następujące warunki są więc równoważne warunkowi
Następujące warunki są więc równoważne warunkowi
 :
:
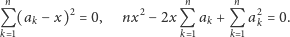 |
Otrzymaliśmy równanie kwadratowe, które, oczywiście, ma jedno
lub dwa rozwiązania w zbiorze liczb zespolonych, przy czym ze wzoru
Viète’a ich średnia arytmetyczna to
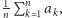 czyli punkt
czyli punkt
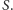
Korzystając z wyżej wykazanej własności zbioru
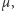 można łatwo
wyprowadzać kolejne. W szczególności, po dokładnym przyjrzeniu
się dowodowi okazuje się, że warunek z definicji można znacząco
osłabić.
można łatwo
wyprowadzać kolejne. W szczególności, po dokładnym przyjrzeniu
się dowodowi okazuje się, że warunek z definicji można znacząco
osłabić.
Wniosek. Niech
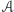 będzie skończonym zbiorem punktów na
płaszczyźnie. Wówczas zbiór
będzie skończonym zbiorem punktów na
płaszczyźnie. Wówczas zbiór
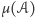 składa się ze wszystkich
takich punktów
składa się ze wszystkich
takich punktów
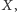 że dla pewnych trzech różnych prostych
że dla pewnych trzech różnych prostych
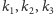 przechodzących przez
przechodzących przez
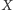 suma kwadratów odległości
punktów z
suma kwadratów odległości
punktów z
 od
od

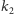 i
i
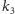 jest taka sama.
jest taka sama.


Poniższe przykłady można rozwiązać przy użyciu układu współrzędnych (sprawdzając wyprowadzone w twierdzeniu warunki), ale łatwiej jest zastosować uzyskane wyniki jakościowe.
Zgodnie ze wspomnianym wnioskiem, aby wykazać należenie
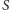 do
zbioru
do
zbioru
 wystarczy zauważyć, że ze względu na symetrię suma
kwadratów odległości od prostych
wystarczy zauważyć, że ze względu na symetrię suma
kwadratów odległości od prostych
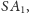
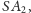
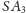 jest taka
sama. Co prawda użyty argument wymaga naprawy dla
jest taka
sama. Co prawda użyty argument wymaga naprawy dla
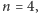 ale na
szczęście ten przypadek został już rozważony. Skoro
ale na
szczęście ten przypadek został już rozważony. Skoro
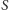 to środek
ciężkości rozważanych punktów, to zgodnie z twierdzeniem jest jedynym
punktem zbioru
to środek
ciężkości rozważanych punktów, to zgodnie z twierdzeniem jest jedynym
punktem zbioru
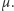
Przykład 3. Zbadajmy zbiór
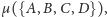 gdzie
gdzie
 jest rombem o kątach
jest rombem o kątach
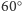 i
i
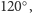 czyli składającym się
z dwóch trójkątów równobocznych. Przyjmijmy, że
czyli składającym się
z dwóch trójkątów równobocznych. Przyjmijmy, że
Zauważmy, że odległości


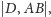
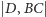 są równe. W związku z tym sumy
kwadratów odległości wierzchołków rombu od prostych
są równe. W związku z tym sumy
kwadratów odległości wierzchołków rombu od prostych
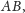
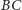 i
i
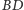 także są równe. Oznacza to, że
także są równe. Oznacza to, że
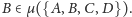 Stosując twierdzenie, otrzymujemy
Stosując twierdzenie, otrzymujemy
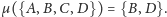
W dalszej części mojej pracy zajmowałem się, między innymi, charakteryzacją
zbiorów o jednoelementowym zbiorze
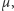 to jest takich, że środek masy
należy do zbioru
to jest takich, że środek masy
należy do zbioru
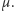 Opisałem także geometryczne znaczenie zbioru
Opisałem także geometryczne znaczenie zbioru
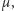 gdy rozważamy zbiór wierzchołków trójkąta. Z możliwych dróg
uogólnienia tego problemu szczególnie ciekawe wydaje mi się postawienie
analogicznych pytań dla zbiorów w wyższych wymiarach. Otrzymane
analitycznie warunki są podobne, ale nie doszedłem do dobrego opisu
klasy takich skończonych zbiorów punktów przestrzeni co najmniej
trójwymiarowej, które mają niepusty zbiór
gdy rozważamy zbiór wierzchołków trójkąta. Z możliwych dróg
uogólnienia tego problemu szczególnie ciekawe wydaje mi się postawienie
analogicznych pytań dla zbiorów w wyższych wymiarach. Otrzymane
analitycznie warunki są podobne, ale nie doszedłem do dobrego opisu
klasy takich skończonych zbiorów punktów przestrzeni co najmniej
trójwymiarowej, które mają niepusty zbiór
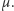 Można też
zastanowić się nad dostosowaniem definicji zbioru
Można też
zastanowić się nad dostosowaniem definicji zbioru
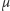 do zbiorów
nieskończonych.
do zbiorów
nieskończonych.


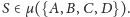
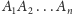


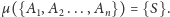
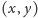 utożsamiać z liczbą zespoloną
utożsamiać z liczbą zespoloną
 Takie przyporządkowanie punktom liczb zespolonych nazywamy
układem współrzędnych zespolonych.
Takie przyporządkowanie punktom liczb zespolonych nazywamy
układem współrzędnych zespolonych.
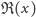 oznacza część rzeczywistą liczby
oznacza część rzeczywistą liczby
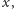 a
a
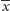 liczbę
sprzężoną z
liczbę
sprzężoną z
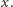
 do
do
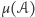 zapiszemy we współrzędnych kartezjańskich, to problem okazuje
się równoważny następującemu:
zapiszemy we współrzędnych kartezjańskich, to problem okazuje
się równoważny następującemu:  i punktu
i punktu
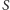 wykazać, że istnieje jedna lub dwie pary punktów
wykazać, że istnieje jedna lub dwie pary punktów
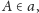
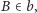 takie że odcinki
takie że odcinki
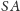 i
i
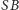 są równe
i prostopadłe.
są równe
i prostopadłe.