Stowarzyszenie na rzecz Edukacji Matematycznej
LXII Olimpiada Matematyczna
W roku szkolnym 2010/2011 Stowarzyszenie na rzecz Edukacji Matematycznej
jest organizatorem LXII edycji Olimpiady Matematycznej. Od września do
grudnia
 roku uczestnicy Olimpiady Matematycznej zmagali się
z dwunastoma zadaniami domowymi pierwszego etapu zawodów
roku uczestnicy Olimpiady Matematycznej zmagali się
z dwunastoma zadaniami domowymi pierwszego etapu zawodów
Do jedenastu Komitetów Okręgowych OM w całym kraju przysłano
do oceny prace
 uczniów. Do zawodów drugiego stopnia
zakwalifikowano 605 uczestników. Omówimy jedno z zadań pierwszego
etapu LXII OM.
uczniów. Do zawodów drugiego stopnia
zakwalifikowano 605 uczestników. Omówimy jedno z zadań pierwszego
etapu LXII OM.
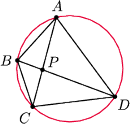
Rys. 2
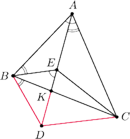
Rys. 3
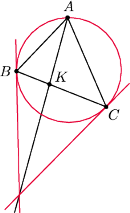
Rys. 4
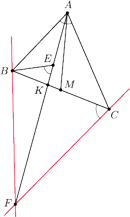
Rys. 5
Z treści rozważanego zadania wynika, że prosta
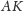 jest symedianą
w
jest symedianą
w
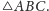 Oznacza to, że prosta
Oznacza to, że prosta
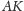 jest obrazem środkowej
jest obrazem środkowej
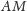 w symetrii osiowej względem dwusiecznej kąta
w symetrii osiowej względem dwusiecznej kąta
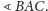 Przedstawimy poniżej dwa inne rozwiązania zadania
Przedstawimy poniżej dwa inne rozwiązania zadania
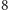 wykorzystujące
własności symedian. Rozwiązania te nie są prostsze niż rozwiązanie już
zaprezentowane, korzystają jednak z ciekawych faktów.
wykorzystujące
własności symedian. Rozwiązania te nie są prostsze niż rozwiązanie już
zaprezentowane, korzystają jednak z ciekawych faktów.
Fakt 1. W czworokącie
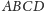 wpisanym
w okrąg przekątne przecinają się w punkcie
wpisanym
w okrąg przekątne przecinają się w punkcie
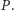 Jeżeli
Jeżeli
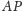 jest
symedianą w
jest
symedianą w
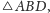 to
to
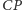 jest symedianą w
jest symedianą w
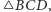
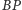 jest symedianą w
jest symedianą w
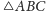 oraz
oraz
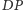 jest symedianą w
jest symedianą w
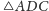 (Rys. 2).
(Rys. 2).
Rozwiązanie zadania 8 oparte na fakcie 1.
Niech
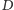 będzie punktem przecięcia prostej
będzie punktem przecięcia prostej
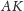 z okręgiem
opisanym na
z okręgiem
opisanym na
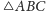 różnym
od punktu
różnym
od punktu
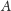 (Rys. 3). Wówczas
(Rys. 3). Wówczas
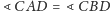 jako kąty
wpisane oparte na tym samym łuku. Ponadto
z założenia
jako kąty
wpisane oparte na tym samym łuku. Ponadto
z założenia
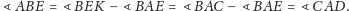 Z faktu
Z faktu
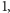
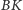 jest symedianą w
jest symedianą w
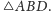 Równość
Równość
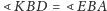 oznacza, że
oznacza, że
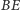 jest środkową w
jest środkową w
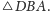 Więc
Więc
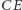 jest środkową
w
jest środkową
w
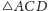 i
i
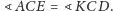 Ponadto
Ponadto
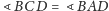 jako kąty wpisane oparte na tym samym łuku.
Ostatecznie
jako kąty wpisane oparte na tym samym łuku.
Ostatecznie
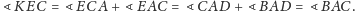
Fakt 2. Jeżeli
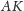 jest symedianą w
jest symedianą w
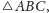 to styczne do
okręgu opisanego na
to styczne do
okręgu opisanego na
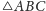 w punktach
w punktach
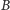 i
i
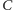 oraz
prosta
oraz
prosta
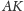 są współpękowe (Rys. 4).
są współpękowe (Rys. 4).
Rozwiązanie zadania 8 oparte na fakcie 2. Niech styczne
do okręgu opisanego na
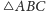 w punktach
w punktach
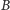 i
i
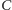 przecinają się w punkcie
przecinają się w punkcie
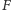 (Rys. 5). Z faktu 2 prosta
(Rys. 5). Z faktu 2 prosta
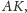 jako symediana w
jako symediana w
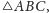 przechodzi przez
przechodzi przez
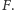 Mamy zatem
Mamy zatem
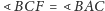 z twierdzenia o kącie pomiędzy styczną i cięciwą.
Z założenia
z twierdzenia o kącie pomiędzy styczną i cięciwą.
Z założenia
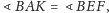 więc punkty
więc punkty
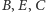 i
i
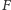 leżą na jednym okręgu. Z równości
leżą na jednym okręgu. Z równości
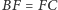 wynika, że
wynika, że
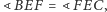 co jest tezą zadania.
co jest tezą zadania.