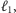
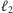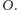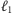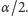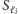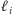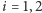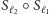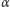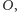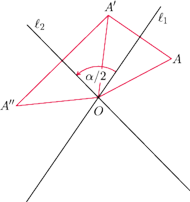
Rozważmy na płaszczyźnie dwie proste przecinające się w punkcie Przypuśćmy, że kąt między tymi prostymi (mierzony od prostej przeciwnie do ruchu wskazówek zegara) ma miarę Niech oznacza symetrię osiową względem prostej ( ). 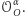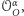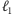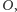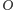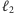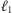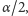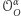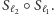Bez trudu możemy zauważyć, że złożenie tych symetrii jest obrotem o kąt wokół punktu który oznaczymy przez Odwrotnie, jeśli mamy dany obrót to wybierając dowolną prostą przechodzącą przez punkt a następnie prowadząc przez prostą tworzącą z  kąt o mierze możemy przedstawić w postaci złożenia symetrii osiowych Tak więc dowolny obrót jest złożeniem dwóch symetrii osiowych o osiach przechodzących przez środek obrotu. Zauważmy przy tym, iż jedna z osi może być wybrana dowolnie.

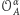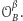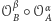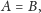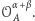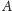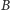Rozważmy dwa obroty oraz Zastanowimy się, jakim przekształceniem jest złożenie tych obrotów. W przypadku, gdy odpowiedź jest natychmiastowa. Otrzymujemy obrót Mniej oczywista jest sytuacja, gdy i  są różnymi punktami.

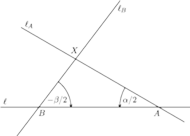
Poprowadźmy przez punkty 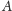i 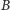 prostą 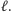Następnie narysujmy

• przez punkt 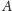prostą 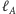tworzącą z prostą 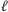kąt o mierze 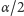(mierzony od prostej ),
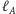• przez punkt 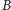prostą 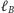tworzącą z prostą 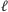kąt o mierze 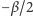(mierzony od prostej ).

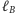Na mocy powyższych uwag rozważane obroty możemy przedstawić w postaci złożenia symetrii osiowych

Tak więc,

gdyż 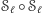jest, oczywiście, przekształceniem tożsamościowym. Teraz staje się jasne, że jeśli proste 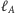i 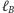 przecinają się w punkcie 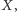to

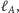
W przypadku, gdy proste 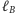są równoległe (ma to miejsce wtedy, gdy 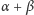jest całkowitą wielokrotnością kąta 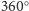), złożenie rozważanych obrotów jest przesunięciem (jako złożenie dwóch symetrii osiowych o osiach równoległych).

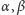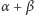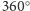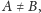Podsumowanie. Jeżeli niezerowe kąty są takie, że nie jest całkowitą wielokrotnością oraz to

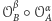
(1)

jest obrotem 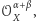gdzie 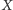jest wierzchołkiem trójkąta 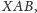takiego że 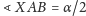i  ;

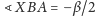(2)

w szczególności jeśli 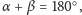to 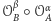jest symetrią środkową względem punktu 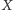(wyznaczonego w analogiczny jak wyżej sposób).

Umowa. 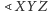oznacza kąt między półprostym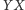i i 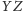 mierzony od półprostej

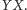
Poniżej przedstawimy kilka zadań, w rozwiązaniach których zastosujemy obroty.