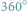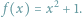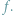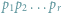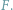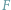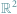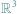Delta mi!

Równania algebraiczne, czyli takie, które można zapisać, przyrównując wielomian do zera, intrygowały ludzi od bardzo dawna. Rozwiązywaniem równań zajmowano się już w czasach starożytnych. W szkole uczą nas, jak rozwiązywać równania liniowe i kwadratowe, to jest takie, w których występuje funkcja liniowa (wielomian stopnia pierwszego) albo funkcja kwadratowa (wielomian stopnia drugiego). Matematycy włoscy podali w XVI wieku wzory na pierwiastki równań stopnia trzeciego i czwartego. A co z równaniami wyższych stopni?

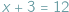Rozwiązywanie równań wymuszało poszerzenie zasobu liczb, jakimi się posługiwano. Równanie można było rozwiązać, posługując się najnaturalniejszymi liczbami, zwanymi zresztą naturalne, ale równanie 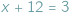wymagało rozszerzenia ich zasobu do liczb całkowitych. Wyjście poza obręb równań pierwszego stopnia pokazało, że do rozwiązania np. równania 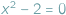nie wystarczą nie tylko liczby całkowite, ale nawet wszystkie liczby wymierne, czyli ułamki 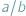zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną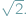

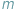Ten artykuł będzie poświęcony zliczaniu różnych kolorowań obiektów, które podlegają symetrii. Wyobraźmy sobie, że Kalina chciałaby pokolorować rogi kwadratu za pomocą kolorów. Ile różnych figur może w ten sposób otrzymać?

Grupa warkoczy była rozważana po raz pierwszy przez Adolfa Hurwitza w roku 1885, jednak nie pod tą nazwą; w grupie rozważanej przez Hurwitza trudno było dopatrzyć się warkoczy. Nazwę wprowadził Emil Artin w roku 1925, bo w jego interpretacji elementy grupy kojarzą się z warkoczami. Przypomnę, jak się je zaplata...

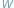Rozważamy wielomian o współczynnikach rzeczywistych stopnia 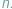Wiadomo, że wielomian taki ma 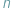pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu 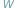należących do wybranego przedziału 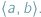Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej 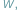znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.

Rozważamy wielomian stopnia o współczynnikach rzeczywistych...

Jednym z najstarszych zagadnień matematyki są równania algebraiczne, wśród nich problem znalezienia pierwiastków trójmianu kwadratowego...

Dodawanie jest łatwe. Każdy się z tym zgodzi. Ot, zapisujemy dodawane liczby jedna pod drugą, dodajemy kolejne cyfry, bacząc na przeniesienia i to wszystko. Gorzej jest z mnożeniem...

Matematyka, zwłaszcza tzw. szkolna, wypracowała przez lata procedury rozwiązywania określonego typu zadań. Gdy rozpoznajemy problem jako równanie kwadratowe, w głowie pojawia się hasło "bekwadratminusczteryace" i już wszystko wiadomo, niezależnie od tego, jak w rzeczywistości nazwaliśmy współczynniki funkcji kwadratowej...

Wbrew często (i zazwyczaj bezmyślnie) powtarzanemu przysłowiu nie każdy obraz jest wart tysiąca słów. Ale niektóre są...

Teoria krat pojawiła się pod koniec XIX wieku, wyrastając z logiki i algebry. W logice kraty pojawiły się za sprawą George’a Boole’a, a w algebrze kraty pierwszy rozpatrywał Richard Dedekind. Kraty są przedmiotem badań algebraików, stanowią jednocześnie wygodny środek opisu znanych struktur matematycznych, których przykłady przedstawię w dalszej części artykułu.

Rozwiąż równanie! – to jedno z najczęściej słyszanych przez ucznia poleceń nauczyciela matematyki. Gdy usłyszymy to polecenie, nie wątpimy, że otrzymane równanie można rozwiązać i że my potrafimy to zrobić. Zresztą o każdym zadaniu matematycznym, na które natrafimy, uważamy, że można je rozwiązać. Jeśli nie widzimy rozwiązania od razu, to pewnie trzeba jeszcze trochę pomyśleć, pokombinować, wynaleźć jakiś sprytny sposób, może poczytać w mądrych książkach i rozwiązanie musi się znaleźć. Czy na pewno tak jest? Okazuje się, że istnieją zadania, niedające się rozwiązać, choć są łudząco podobne do innych, które rozwiązujemy bez trudu.

Za pomocą kolorowania wielomianów można udowodnić Zasadnicze twierdzenie algebry w zaskakująco elementarny sposób...

30 maja 1832 roku w Paryżu zginął w pojedynku młody matematyk, Evariste Galois. Nie ma pewności, czy pojedynek ten miał podłoże polityczne, czy też Galois bronił honoru pewnej młodej damy. W pożegnalnym liście poprosił on, by jego notatki wysłać Jacobiemu albo Gaussowi. Żaden z tych wielkich matematyków nigdy nie zobaczył jednak zapisków Galois.

Wyobraźmy sobie igłę umieszczoną wewnątrz pewnego zbioru na płaszczyźnie. Igłę traktujemy jak odcinek jednostkowy, który możemy dowolnie obracać i przesuwać w obrębie naszego zbioru. Załóżmy, że chcielibyśmy wykonać igłą obrót o  – jak wiele miejsca do tego potrzeba?

Niejeden maturzysta marzy zapewne, żeby na egzaminie dojrzałości rozwiązywać następujące, z pozoru błahe, zadanie: Wyznacz liczbę miejsc zerowych funkcji Abiturienta nie zraziłaby prawdopodobnie nawet drobna przeszkoda, jaką jest wyraźny brak informacji o dziedzinie funkcji  Z uwagi na wszechobecność zbioru liczb rzeczywistych w obecnym programie nauczania wydaje się, że o żadnych zerach mowy być nie może. Nawet słynna „delta” nie jest tu potrzebna.

Twierdzenie o jednoznaczności rozkładu na czynniki pierwsze w zbiorze liczb naturalnych wypowiada się najprościej w następujący sposób: każdą liczbę naturalną różną od jedności możemy przedstawić w postaci iloczynu  liczb pierwszych na jeden tylko sposób, o ile rozkłady, różniące się kolejnością czynników, uważać będziemy za równe...

W tym artykule będziemy się zajmowali obliczaniem wyznaczników macierzy w dowolnym skończonym ciele  Będziemy także badali, jakie jest prawdopodobieństwo, że taki wyznacznik dla macierzy z losowo wpisanymi elementami z ciała  jest różny od  oraz jakie jest prawdopodobieństwo, że w losowym grafie skierowanym jest nieparzyście wiele pokryć cyklowych.

Jeśli chcemy rozwiązać układ równań – taki zwykły, dwa równania liniowe z dwiema niewiadomymi – za pomocą komputera, całkiem wygodnie jest użyć metody wyznaczników...

Każdy uczeń szkoły średniej wie, że gdy zna się współczynniki trójmianu kwadratowego, to można jawnymi wzorami wyrazić pierwiastki tego trójmianu. We wzorach tych wykonuje się (skończoną liczbę razy) tylko cztery działania arytmetyczne i pierwiastkowanie.

Jak wiele innych ważnych twierdzeń matematyki, zasadnicze twierdzenie algebry, udowodnione przez Carla Friedricha Gaussa w ostatnim roku osiemnastego stulecia, informuje nas, że pewne obiekty nie istnieją. Mianowicie, nie ma takiego, różnego od stałej, wielomianu zmiennej zespolonej, który nie znikałby w żadnym punkcie płaszczyzny zespolonej

Płaszczyznę można wyposażyć w działania dodawania i mnożenia jej punktów. Dlaczego nie można tego zrobić z przestrzenią ?

Na ile sposobów można przykryć banknotem prostokąt o tych samych rozmiarach? xxx Każdy od razu zgadnie, że na cztery sposoby: do góry orłem, przy czym orzeł może być do dołu lub do góry nogami, i podobnie na dwa sposoby królem do góry (choć na banknocie nie widać jego nóg).

Przyjmijmy, że słowem będzie dla nas dowolny ciąg liter. Nie tylko taki, który da się wymówić albo którego znaczenie jest objaśnione w słowniku. Zupełnie dowolny ciąg, złożony z jednej litery, kilku lub nawet długości całej encyklopedii.