Czwórkę punktów nazywamy układem ortocentrycznym, gdy każde dwa z nich wyznaczają prostą prostopadłą do prostej wyznaczonej przez pozostałe dwa.

Powyższa definicja jest konsekwencją pewnego rodzaju równouprawnienia: jeśli punkt 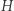jest ortocentrum nieprostokątnego trójkąta 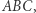to każdy z punktów 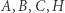jest ortocentrum trójkąta wyznaczonego przez trzy pozostałe. Gdy zachodzą dwie z prostopadłości, o których mowa w definicji, to trzecia również - wynika to z tego, że każdy trójkąt ma ortocentrum.

Układy ortocentryczne pojawiają się zatem w naturalny sposób w wielu konfiguracjach geometrycznych. W zadaniu 1 poznajemy kilka własności układów ortocentrycznych, a w zadaniach 2 i 3 uczymy się je rozpoznawać.

Ze względu na wspomniane wcześniej równouprawnienie, spodki wysokości trójkąta 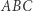możemy nazwać po prostu spodkami układu ortocentrycznego 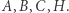Są to spodki wysokości każdego z trójkątów: 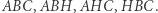Punkty 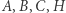wyznaczają sześć odcinków, które będziemy nazywać odcinkami układu ortocentrycznego. Każdy z nich jest średnicą okręgu przechodzącego przez pewne dwa spodki, co wynika z odpowiednich prostopadłości. Korzystamy z tego w zadaniach 1(e) oraz 4-6.

Należy jeszcze wspomnieć o zdegenerowanym układzie ortocentrycznym. W przypadku trójkąta 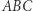z kątem prostym przy wierzchołku 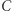mamy 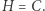Jest oczywiste, że 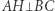i 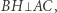trudno natomiast mówić o prostej 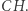Można jednak z całą pewnością stwierdzić, że istnieje prosta prostopadła do 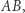na której leżą punkty 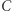i