Co to jest?

Pierścień

Jednym z fundamentalnych pojęciem algebraicznych są pierścienie. Zostały one wprowadzone pod koniec XIX wieku z nadzieją na pomoc w udowodnieniu Wielkiego Twierdzenia Fermata. Jak wiadomo, zostało to uczynione dopiero w 1995 roku, więc przez długi czas nadzieja ta była płonna...

Modelowym przykładem pierścienia jest zbiór liczb całkowitych 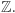$|Z.$ Formalnie, pierścień przemienny 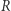$R$ to zbiór z działaniami dodawania, odejmowania i mnożenia, przy czym spełnione są naturalne własności: 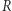$|R$ z dodawaniem i odejmowaniem jest grupą, jest rozdzielność mnożenia względem dodawania, a mnożenie jest łączne i przemienne i posiada jedynkę.

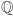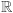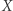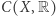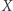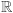Inne przykłady pierścieni przemiennych to $|Q$ lub $R$ z naturalnymi działaniami. Przykład z innej półki: jeśli $X$ jest przestrzenią metryczną (patrz artykuł o przestrzeniach metrycznych z tego numeru Delty) lub ogólniej przestrzenią topologiczną, to zbiór $,R) |C(X$ wszystkich ciągłych funkcji z $|X$ do $|R$ jest pierścieniem przemiennym.

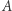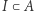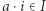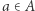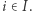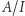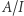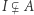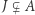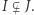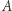Ideał w pierścieniu przemiennym $| A$ jest to podgrupa $| I⊂ A$ taka, że $|a⋅i ∈I$ dla wszystkich $a ∈ A$ oraz $i |∈ I.$ Ten warunek gwarantuje, że w zbiorze $A/I$ da się sensownie mnożyć; tzn. że $A/I |$ jest pierścieniem przemiennym. W tym sensie ideał odpowiada podgrupie normalnej. Ideał $| I⊊ A$ jest maksymalny, jeśli nie istnieje ideał $| J⊊ A$ taki, że $| I ⊊J.$ Każde $|A$ posiada przynajmniej dwa ideały: 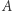$A |$ oraz ${0}. 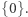|$ Mówimy, że 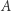$A$ jest ciałem, jeśli nie posiada żadnych innych ideałów, np. 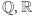$Q, R$ są ciałami, lecz 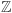$|Z$ nie jest ciałem.

Jeśli 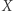$X$ jest przestrzenią topologiczną i 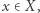$, |x∈ X$ to podzbiór

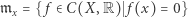
,R) f(x)=0} 𝔪x = { f ∈C(X

jest ideałem maksymalnym. Co więcej, jeśli 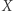$X$ jest zwartą przestrzenią (dla przestrzeni metrycznej zwartość oznacza, że każdy ciąg zawiera podciąg zbieżny), są to jedyne ideały maksymalne w 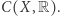$,R). C(X$ Zatem jeśli ktoś roztargniony zgubi swoją ulubioną przestrzeń topologiczną 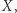$, X$ ale będzie pamiętać, jaki jest pierścień 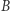$|B$ funkcji ciągłych na tej przestrzeni, to może zrekonstruować 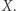$. 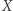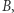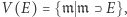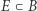|X$ Mianowicie, punktami $|X$ będą ideały maksymalne w $B,$ a zbiory domknięte to zbiory ideałów maksymalnych postaci $|V(E) = {𝔪 𝔪 ⊃ E},$ gdzie $|E⊂ B$ jest podzbiorem.

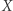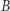W latach pięćdziesiątych Alexandre Grothendieck zaproponował, by tę operację "odzyskiwania" $X$ z $B$ przeprowadzać dla dowolnego pierścienia 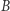$B$ ; niekoniecznie pochodzącego od 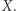$. X$ Doprowadziło to do powstania teorii schematów, która ostatecznie miała wielki udział m.in. w dowodzie Wielkiego Twierdzenia Fermata. Po stu latach pierścienie miały swój rewanż!