Drobiazgi
Skąd mógł to wiedzieć?
W 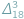 (Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...
(Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...
Warto zauważyć, że takie wizjonerskie przedstawianie matematycznych faktów trafiało się wielokrotnie. Zbiorem takich wizji jest ogromne dzieło Diofantosa (które będzie przywołane w 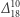 ) powstałe dwa tysiące lat temu, a dotyczące teorii liczb.
) powstałe dwa tysiące lat temu, a dotyczące teorii liczb.
W szczególności znajduje się tam stwierdzenie, że dla dowolnych liczb całkowitych 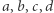 wyrażenie
wyrażenie 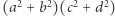 też da się przedstawić jako suma kwadratów dwóch liczb całkowitych i to na dwa sposoby. Zamiast dowodu jest tam po prostu napisane, jakie są to liczby:
też da się przedstawić jako suma kwadratów dwóch liczb całkowitych i to na dwa sposoby. Zamiast dowodu jest tam po prostu napisane, jakie są to liczby: 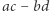 i
i 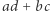 lub
lub 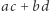 i
i 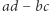 ; dla przykładu, biorąc 2, 4, 3 i 5, otrzymamy
; dla przykładu, biorąc 2, 4, 3 i 5, otrzymamy

proszę sprawdzić.
Dziś ta prawidłowość kojarzy się z twierdzeniem o liczbach zespolonych, które mówi, że moduł iloczynu równa się iloczynowi modułów, ale jak mógł to dostrzec Diofantos?