Drobiazgi
Dlaczego pierwiastek z 2. nie pasuje do liczb wymiernych?
Zupełnie nieszokująca zasada dobrego uporządkowania mówi, że każdy niepusty podzbiór liczb naturalnych ma element najmniejszy. Pokażemy, jak ją wykorzystać do wykazania, że 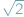 jest niewymierne, czyli że dla żadnej liczby naturalnej
jest niewymierne, czyli że dla żadnej liczby naturalnej 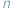 liczba
liczba 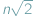 nie jest całkowita.
nie jest całkowita.
Niech 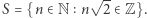 Załóżmy, że zbiór
Załóżmy, że zbiór 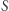 jest niepusty. Oczywiście,
jest niepusty. Oczywiście, 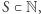 więc z zasady dobrego uporządkowania zbiór
więc z zasady dobrego uporządkowania zbiór 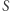 ma element najmniejszy (być może nie jest on jedyny). Niech tym elementem będzie
ma element najmniejszy (być może nie jest on jedyny). Niech tym elementem będzie 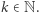 Rozważmy następującą liczbę:
Rozważmy następującą liczbę: 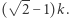 Skoro
Skoro 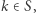 to
to 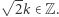 Zatem
Zatem 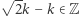 oraz
oraz

Zauważmy, że 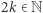 oraz
oraz 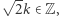 więc
więc 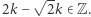 W takim razie
W takim razie 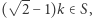 ale
ale 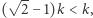 a założyliśmy, że
a założyliśmy, że 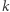 jest elementem najmniejszym ze zbioru
jest elementem najmniejszym ze zbioru 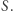 Zatem otrzymujemy sprzeczność z założeniem, że
Zatem otrzymujemy sprzeczność z założeniem, że 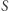 jest niepustym zbiorem.
jest niepustym zbiorem.