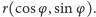Liczby zespolone czterema sposobami
Jeżeli określimy dodawanie i mnożenie punktów płaszczyzny, z wyróżnionymi punktami 0 i 1, w sposób przedstawiony na rysunku, to otrzymamy liczby zespolone...
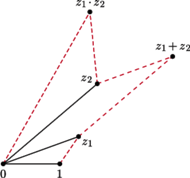
Suma to taki punkt, że 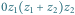 jest równoległobokiem; iloczyn to taki punkt, że trójkąty
jest równoległobokiem; iloczyn to taki punkt, że trójkąty  i
i 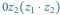 są podobne i mają tę samą orientację.
są podobne i mają tę samą orientację.
Ten szybki, jasny sposób wprowadzenia liczb zespolonych - zwany geometrycznym - okazał się jednak mało praktyczny. Spójrzmy teraz na te liczby inaczej, jak na wektory o początku w 0. Ponieważ wszystkie mają ten sam początek, więc będziemy je nazywać tak jak ich końce. Każdy z nich może być uzyskany z wektora 1 za pomocą podobieństwa spiralnego o środku 0 (podobieństwo spiralne to złożenie jednokładności i obrotu o tym samym środku; jedynie wtedy obojętna jest kolejność wykonywania tych przekształceń). Dodawanie liczb zespolonych w tej postaci - nazwijmy ją wektorową - to składanie przesunięć odpowiadających składnikom, natomiast mnożenie to składanie podobieństw spiralnych (proszę na rysunku sprawdzić, że wektor 1 przy wykonaniu podobieństw spiralnych, odpowiadających 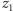 i
i 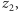 stanie się wektorem
stanie się wektorem 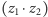 ).
).
Takie ujęcie liczb zespolonych pozwala zauważyć, że każda z nich jest określona przez liczbę  mówiącą, ile razy musiał się przedłużyć wektor 1, aby ją otrzymać i liczbę
mówiącą, ile razy musiał się przedłużyć wektor 1, aby ją otrzymać i liczbę 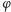 mówiącą, o jaki kąt wektor 1 musiał się obrócić. Pierwszą z tych liczb nazywamy modułem liczby zespolonej, a drugą argumentem. Jeżeli przedstawimy liczbę zespoloną w postaci
mówiącą, o jaki kąt wektor 1 musiał się obrócić. Pierwszą z tych liczb nazywamy modułem liczby zespolonej, a drugą argumentem. Jeżeli przedstawimy liczbę zespoloną w postaci 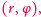 to - wobec powyższych uwag - wzór na mnożenie będzie wyglądał tak:
to - wobec powyższych uwag - wzór na mnożenie będzie wyglądał tak:

Przetłumaczenie tego na zwykłe współrzędne kartezjańskie daje (bez rachunków!) wzór zwany nazwiskiem de Moivre'a

co łatwo się uogólnia na wzory mówiące o potęgowaniu i pierwiastkowaniu liczb zespolonych.
Trzecia postać liczb zespolonych to przedstawienie ich bezpośrednio za pomocą współrzędnych kartezjańskich. Dodawanie ma wówczas bardzo prostą postać

bo tak się przecież dodaje wektory. Natomiast wzór de Moivre'a pozwala zobaczyć, że i wzór na mnożenie nie jest wiele bardziej skomplikowany:
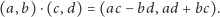 |
(1) |
Dowód. Jeśli 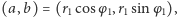 a
a 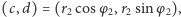 to
to

Można uczynić teraz dwie obserwacje. Pierwsza to ta, że każda liczba zespolona da się przedstawić jako

Zauważmy, że  to po prostu 1 - każdy może sprawdzić, jak się przez
to po prostu 1 - każdy może sprawdzić, jak się przez  mnoży. Natomiast
mnoży. Natomiast

co jest zwykłą minus jedynką, i to też można sprawdzić mnożąc. Liczba  jest oznaczana przez
jest oznaczana przez 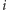 (od imaginarius), nazywana jednostką urojoną i stanowi wielką tajemnicę dla różnego rodzaju filozofów (bo jak to możliwe, aby kwadrat był ujemny...). Tak algebraicznie ujęte liczby zespolone to sumy
(od imaginarius), nazywana jednostką urojoną i stanowi wielką tajemnicę dla różnego rodzaju filozofów (bo jak to możliwe, aby kwadrat był ujemny...). Tak algebraicznie ujęte liczby zespolone to sumy 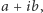 gdzie
gdzie 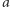 i
i 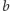 to liczby rzeczywiste. Rachunki na nich przeprowadza się tak jak na wielomianach, pamiętając zawsze, że
to liczby rzeczywiste. Rachunki na nich przeprowadza się tak jak na wielomianach, pamiętając zawsze, że 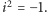 Na przykład wzór na mnożenie wyprowadza się przy tej interpretacji tak:
Na przykład wzór na mnożenie wyprowadza się przy tej interpretacji tak:

Jest to najstarszy i najczęściej stosowany sposób używania liczb zespolonych.
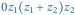 jest równoległobokiem; iloczyn to taki punkt, że trójkąty
jest równoległobokiem; iloczyn to taki punkt, że trójkąty 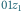 i
i 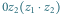 są podobne i mają tę samą orientację.
są podobne i mają tę samą orientację.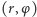 ma, jak łatwo zauważyć, współrzędne kartezjańskie
ma, jak łatwo zauważyć, współrzędne kartezjańskie 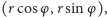 czyli
czyli