Symetrie ciał i grupy: teoria Galois

Poniższa opowieść była na tyle ważna dla młodego, zaledwie dwudziestoletniego, matematyka Évariste'a Galois, że poświęcił ostatni dzień przed pojedynkiem, aby spisać ją w liście do przyjaciela. Niestety, nie dostał od losu szansy na kontynuowanie swoich prac, ale jakiś czas po jego śmierci matematycy zrozumieli znaczenie jego pomysłów. Ślady teorii, z której zarysem Czytelnik zapoznać się może w dalszej części artykułu, odnaleźć można w wielu gałęziach współczesnej matematyki. Jej bezpośrednim następstwem jest wiele efektownych rozwiązań problemów, których ludzkość szukała przez setki lat: nierozwiązalność (przez pierwiastniki) równań wielomianowych stopnia 5 lub wyższego, niekonstruowalność pewnych wielokątów foremnych (cyrklem i linijką), a także niewykonalność klasycznych konstrukcji geometrycznych, czyli podwojenia sześcianu, trysekcji kąta i kwadratury koła.
Pierwiastki wielomianów.
Zbiór liczb wymiernych 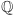 jest przydatny i przyjazny użytkownikowi, ale jednak mocno wybrakowany. Zwykle dostrzegamy jego braki, patrząc na dopuszczalne rozwinięcia dziesiętne: liczby wymierne mogą mieć tylko skończone lub okresowe od pewnego miejsca rozwinięcia. Tym razem spójrzmy na ten problem z punktu widzenia wielomianów. Znajdźmy, na przykład, pierwiastki wielomianu
jest przydatny i przyjazny użytkownikowi, ale jednak mocno wybrakowany. Zwykle dostrzegamy jego braki, patrząc na dopuszczalne rozwinięcia dziesiętne: liczby wymierne mogą mieć tylko skończone lub okresowe od pewnego miejsca rozwinięcia. Tym razem spójrzmy na ten problem z punktu widzenia wielomianów. Znajdźmy, na przykład, pierwiastki wielomianu 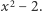 Dostajemy dwie możliwości:
Dostajemy dwie możliwości: 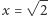 i
i 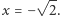 Żadna z nich nie jest liczbą wymierną - przeczyłoby to podstawowym własnościom podzielności. Stąd wniosek, że zbiór
Żadna z nich nie jest liczbą wymierną - przeczyłoby to podstawowym własnościom podzielności. Stąd wniosek, że zbiór 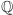 jest za mały, żebyśmy mogli znaleźć wewnątrz niego rozwiązania dla wszystkich równań wielomianowych mających wymierne współczynniki, czyli w pewnym sensie pochodzących od tego zbioru.
jest za mały, żebyśmy mogli znaleźć wewnątrz niego rozwiązania dla wszystkich równań wielomianowych mających wymierne współczynniki, czyli w pewnym sensie pochodzących od tego zbioru.
Ta własność potrafi dawać jeszcze ciekawszy efekt: jeśli chcemy znaleźć pierwiastki wielomianu 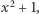 to musimy wyjść poza zbiór liczb rzeczywistych. Rozwiązaniami są jednostka urojona
to musimy wyjść poza zbiór liczb rzeczywistych. Rozwiązaniami są jednostka urojona 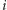 oraz liczba do niej przeciwna
oraz liczba do niej przeciwna 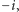 tak zwane pierwiastki kwadratowe z minus jedynki. Widzimy zatem, że pewne liczby niewymierne, a nawet nierzeczywiste, pojawiają się naturalnie w okolicach zbioru liczb wymiernych za sprawą wielomianów.
tak zwane pierwiastki kwadratowe z minus jedynki. Widzimy zatem, że pewne liczby niewymierne, a nawet nierzeczywiste, pojawiają się naturalnie w okolicach zbioru liczb wymiernych za sprawą wielomianów.
Rozszerzenia ciał.
W tej sytuacji wygodnie byłoby rozważać zbiór liczb wymiernych z dodanymi 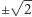 lub
lub 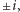 lub innym zestawem pierwiastków pewnego wielomianu. Tylko trzeba odpowiednio się za to zabrać - zadbać o zachowanie pewnych podstawowych własności algebraicznych. O zbiorze
lub innym zestawem pierwiastków pewnego wielomianu. Tylko trzeba odpowiednio się za to zabrać - zadbać o zachowanie pewnych podstawowych własności algebraicznych. O zbiorze 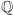 mówimy, że jest ciałem, co oznacza, że jego elementy możemy dodawać, odejmować, mnożyć i dzielić (z wyjątkiem zera, przez które nie chcemy dzielić), i w wyniku tych działań zawsze otrzymujemy elementy tego samego zbioru, liczby wymierne. Jeśli teraz chcemy rozszerzyć ciało
mówimy, że jest ciałem, co oznacza, że jego elementy możemy dodawać, odejmować, mnożyć i dzielić (z wyjątkiem zera, przez które nie chcemy dzielić), i w wyniku tych działań zawsze otrzymujemy elementy tego samego zbioru, liczby wymierne. Jeśli teraz chcemy rozszerzyć ciało 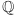 o pewien element, to wymagamy, żeby efektem takiej operacji też było ciało. To oznacza, że będziemy rozważać zbiór otrzymany ze wszystkich możliwych wyników kombinacji czterech podstawowych działań na liczbach wymiernych i dodanym elemencie (lub elementach). Na przykład, jeśli rozszerzamy
o pewien element, to wymagamy, żeby efektem takiej operacji też było ciało. To oznacza, że będziemy rozważać zbiór otrzymany ze wszystkich możliwych wyników kombinacji czterech podstawowych działań na liczbach wymiernych i dodanym elemencie (lub elementach). Na przykład, jeśli rozszerzamy 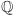 o
o 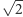 (lub o
(lub o 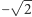 ), to otrzymujemy ciało oznaczane
), to otrzymujemy ciało oznaczane 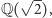 które składa się ze wszystkich liczb postaci
które składa się ze wszystkich liczb postaci 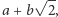 gdzie
gdzie 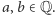 Czytelnik Wnikliwy sprawdzi, że suma, różnica, iloczyn i iloraz dwóch liczb tej postaci również jest tej postaci.
Czytelnik Wnikliwy sprawdzi, że suma, różnica, iloczyn i iloraz dwóch liczb tej postaci również jest tej postaci.
Ogólnie, rozszerzenie 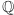 o liczby
o liczby 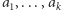 oznaczamy
oznaczamy 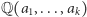 i definiujemy jako najmniejszy zbiór zamknięty na operacje dodawania, odejmowania, mnożenia i dzielenia zawierający cały zbiór
i definiujemy jako najmniejszy zbiór zamknięty na operacje dodawania, odejmowania, mnożenia i dzielenia zawierający cały zbiór 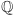 oraz
oraz 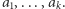 Jeśli
Jeśli 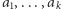 są pierwiastkami pewnych wielomianów o współczynnikach wymiernych, to będziemy je nazywać elementami algebraicznymi nad
są pierwiastkami pewnych wielomianów o współczynnikach wymiernych, to będziemy je nazywać elementami algebraicznymi nad 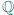 , a rozszerzenie
, a rozszerzenie 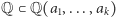 - rozszerzeniem algebraicznym.
- rozszerzeniem algebraicznym.
Stopień rozszerzenia.
Przyjrzyjmy się dokładniej rozszerzeniom 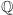 o jeden element algebraiczny nad
o jeden element algebraiczny nad 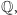 czyli ciałom postaci
czyli ciałom postaci 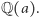 To ograniczenie okazuje się w pełni uprawnione, ponieważ, jak mówi twierdzenie Abela, dowolne rozszerzenie algebraiczne można przedstawić jako rozszerzenie o jeden element. Znalezienie go może nie być łatwe, ale istnieją też proste przypadki.
To ograniczenie okazuje się w pełni uprawnione, ponieważ, jak mówi twierdzenie Abela, dowolne rozszerzenie algebraiczne można przedstawić jako rozszerzenie o jeden element. Znalezienie go może nie być łatwe, ale istnieją też proste przypadki.
Na przykład ciało 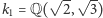 jest tym samym co
jest tym samym co 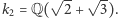 Oczywiście
Oczywiście 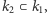 ponieważ
ponieważ 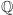 i element
i element 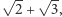 który generuje rozszerzenie, należą do
który generuje rozszerzenie, należą do 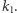 A jak sprawdzić, że
A jak sprawdzić, że 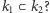 Wystarczy przedstawić
Wystarczy przedstawić 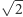 i
i 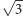 jako elementy
jako elementy 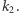 Zauważmy, że
Zauważmy, że 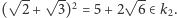 Ponieważ mamy do dyspozycji wszystkie liczby wymierne i podstawowe działania, więc możemy otrzymać
Ponieważ mamy do dyspozycji wszystkie liczby wymierne i podstawowe działania, więc możemy otrzymać 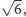 nie wychodząc poza
nie wychodząc poza 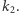 Spójrzmy na wynik mnożenia
Spójrzmy na wynik mnożenia 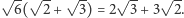 Odejmując od niego dwu- lub trzykrotność
Odejmując od niego dwu- lub trzykrotność 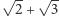 i dzieląc przez liczbę całkowitą, dowiadujemy się, że
i dzieląc przez liczbę całkowitą, dowiadujemy się, że 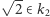 i
i 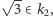 a zatem
a zatem 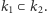
Dlaczego wolimy pracować z rozszerzeniami o jeden element? W tej sytuacji łatwiej jest opisać postać wszystkich elementów rozszerzenia algebraicznego i określić pewne jego parametry. Z definicji element 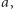 o który rozszerzamy
o który rozszerzamy 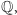 jest pierwiastkiem wielomianu o współczynnikach w
jest pierwiastkiem wielomianu o współczynnikach w 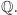 Ale takich wielomianów może być wiele… Na przykład,
Ale takich wielomianów może być wiele… Na przykład, 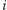 jest pierwiastkiem
jest pierwiastkiem 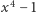 (czyli jest pierwiastkiem 4 stopnia z 1), ale ten wielomian możemy zapisać jako iloczyn
(czyli jest pierwiastkiem 4 stopnia z 1), ale ten wielomian możemy zapisać jako iloczyn 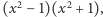 gdzie
gdzie 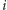 jest pierwiastkiem drugiego czynnika. Który więc wybrać? Wystarczy powiedzieć, że bierzemy wielomian (o współczynnikach wymiernych) najniższego możliwego stopnia, którego
jest pierwiastkiem drugiego czynnika. Który więc wybrać? Wystarczy powiedzieć, że bierzemy wielomian (o współczynnikach wymiernych) najniższego możliwego stopnia, którego 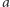 jest pierwiastkiem; nazwiemy go wielomianem minimalnym dla
jest pierwiastkiem; nazwiemy go wielomianem minimalnym dla 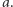 To określa go jednoznacznie z dokładnością do mnożenia przez stałą, więc wybieramy zawsze ten, który ma współczynnik przy najwyższej potędze zmiennej
To określa go jednoznacznie z dokładnością do mnożenia przez stałą, więc wybieramy zawsze ten, który ma współczynnik przy najwyższej potędze zmiennej  równy 1.
równy 1.
Stopniem rozszerzenia 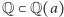 będziemy nazywać po prostu stopień wielomianu minimalnego dla
będziemy nazywać po prostu stopień wielomianu minimalnego dla 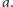 Ta liczba określa również liczbę różnych potęg
Ta liczba określa również liczbę różnych potęg 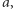 których musimy użyć, żeby opisać wszystkie elementy ciała
których musimy użyć, żeby opisać wszystkie elementy ciała 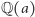 bez dodatkowych mnożeń przez liczby inne niż wymierne. Można powiedzieć, że stopień rozszerzenia
bez dodatkowych mnożeń przez liczby inne niż wymierne. Można powiedzieć, że stopień rozszerzenia 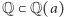 to wymiar
to wymiar 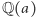 jako przestrzeni liniowej nad
jako przestrzeni liniowej nad 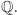 Dokładniej, jeśli
Dokładniej, jeśli 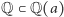 jest rozszerzeniem stopnia
jest rozszerzeniem stopnia 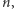 to wszystkie elementy
to wszystkie elementy 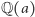 są postaci
są postaci 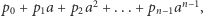 gdzie
gdzie 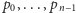 są liczbami wymiernymi. Argument opiera się na spostrzeżeniu, że
są liczbami wymiernymi. Argument opiera się na spostrzeżeniu, że 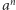 umiemy tak przedstawić - w końcu
umiemy tak przedstawić - w końcu 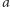 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 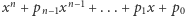 o współczynnikach z
o współczynnikach z 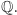
Wobec tego rozszerzenie 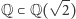 jest stopnia 2, a wielomianem minimalnym dla
jest stopnia 2, a wielomianem minimalnym dla 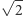 jest
jest 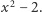 Podobnie
Podobnie 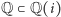 jest rozszerzeniem stopnia 2. A czy rozszerzenie
jest rozszerzeniem stopnia 2. A czy rozszerzenie 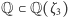 o pierwiastek trzeciego stopnia z 1 (czyli pierwiastek wielomianu
o pierwiastek trzeciego stopnia z 1 (czyli pierwiastek wielomianu 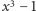 ) jest stopnia 3? Otóż nie - to również jest rozszerzenie stopnia 2. Wielomian
) jest stopnia 3? Otóż nie - to również jest rozszerzenie stopnia 2. Wielomian 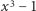 można rozłożyć na czynniki
można rozłożyć na czynniki 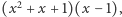 a pierwiastkami pierwszego czynnika są
a pierwiastkami pierwszego czynnika są 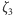 i
i 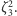 Zatem
Zatem 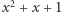 jest wielomianem minimalnym dla
jest wielomianem minimalnym dla 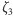 i dla
i dla 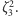
Jeszcze ciekawszy przykład.
Czy podobnie jest z pierwiastkiem trzeciego stopnia z 2? Nie, tym razem dostajemy rozszerzenie 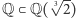 stopnia 3, a wielomian minimalny dla
stopnia 3, a wielomian minimalny dla 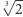 to
to 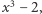 którego pozostałymi pierwiastkami są
którego pozostałymi pierwiastkami są 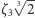 i
i 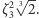 Zauważmy jednak, że
Zauważmy jednak, że 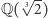 nie zawiera tych dwóch pozostałych pierwiastków - to ciało jest zawarte w ciele liczb rzeczywistych, do którego
nie zawiera tych dwóch pozostałych pierwiastków - to ciało jest zawarte w ciele liczb rzeczywistych, do którego 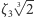 i
i 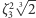 nie należą. Żeby otrzymać najmniejsze ciało zawierające wszystkie pierwiastki
nie należą. Żeby otrzymać najmniejsze ciało zawierające wszystkie pierwiastki 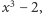 tak zwane ciało rozkładu tego wielomianu, trzeba rozszerzyć
tak zwane ciało rozkładu tego wielomianu, trzeba rozszerzyć 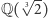 o pozostałe pierwiastki (wystarczy wziąć jeden z nich). Tak samo, jak wcześniej rozszerzaliśmy
o pozostałe pierwiastki (wystarczy wziąć jeden z nich). Tak samo, jak wcześniej rozszerzaliśmy 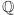 o pewne elementy algebraiczne, możemy rozszerzać dowolne inne ciało!
o pewne elementy algebraiczne, możemy rozszerzać dowolne inne ciało!
Możemy też obliczyć stopień takiego rozszerzenia 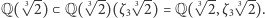 W tym celu trzeba znaleźć wielomian minimalny dla
W tym celu trzeba znaleźć wielomian minimalny dla 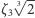 o współczynnikach w
o współczynnikach w 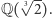 Oczywistym kandydatem jest
Oczywistym kandydatem jest 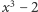 ; ma współczynniki z dobrego ciała, jednak okazuje się za duży. Ale jeśli podzielimy go przez
; ma współczynniki z dobrego ciała, jednak okazuje się za duży. Ale jeśli podzielimy go przez 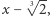 to dostaniemy szukany wielomian minimalny:
to dostaniemy szukany wielomian minimalny: 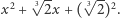 To oznacza, że badane rozszerzenie jest stopnia 2. Możemy też popatrzeć na oba rozszerzenia razem, czyli na wieżę rozszerzeń
To oznacza, że badane rozszerzenie jest stopnia 2. Możemy też popatrzeć na oba rozszerzenia razem, czyli na wieżę rozszerzeń 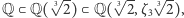 i, zapominając o środkowym ciele, rozważyć rozszerzenie
i, zapominając o środkowym ciele, rozważyć rozszerzenie 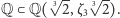 Ponieważ stopnie rozszerzeń w wieżach się mnożą, to rozszerzenie jest stopnia 6.
Ponieważ stopnie rozszerzeń w wieżach się mnożą, to rozszerzenie jest stopnia 6.
Symetrie, czyli automorfizmy.
Jak zauważyliśmy wcześniej, rozszerzenie 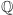 o
o 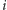 oraz o
oraz o 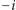 są tym samym. Co więcej, położenia tych elementów w ciele
są tym samym. Co więcej, położenia tych elementów w ciele 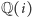 są w pewnym sensie symetryczne. Dokładniej, umiemy tak przekształcić ciało
są w pewnym sensie symetryczne. Dokładniej, umiemy tak przekształcić ciało 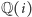 na nie samo, żeby zamienić
na nie samo, żeby zamienić 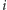 z
z 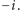 Oczywiście, to nie może być byle jakie przekształcenie - wymagamy, żeby było bijekcją i respektowało strukturę ciała, czyli podstawowe operacje. Przekształcenie
Oczywiście, to nie może być byle jakie przekształcenie - wymagamy, żeby było bijekcją i respektowało strukturę ciała, czyli podstawowe operacje. Przekształcenie 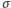 musi zachowywać sumę:
musi zachowywać sumę: 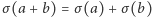 dla dowolnych
dla dowolnych 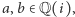 i analogicznie dla odejmowania, mnożenia i dzielenia (a stąd
i analogicznie dla odejmowania, mnożenia i dzielenia (a stąd 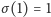 i
i 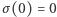 ). Takie przekształcenie ciała nazywamy jego automorfizmem. W przypadku
). Takie przekształcenie ciała nazywamy jego automorfizmem. W przypadku 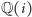 okazuje się, że żądane własności ma sprzężenie liczb zespolonych:
okazuje się, że żądane własności ma sprzężenie liczb zespolonych: 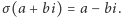 Zauważmy, że ten automorfizm trzyma w miejscu liczby wymierne: dla każdego
Zauważmy, że ten automorfizm trzyma w miejscu liczby wymierne: dla każdego 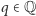 mamy
mamy 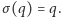
I tu pojawia się kolejna struktura algebraiczna: grupa. Spójrzmy na zbiór wszystkich automorfizmów wybranego ciała - możemy je składać i odwracać! Nietrudno sprawdzić, że przy obu tych operacjach będziemy dostawać przekształcenia zachowujące podstawowe działania. Mamy też automorfizm trywialny, przeprowadzający każdy element na niego samego; składanie z nim nic nie zmienia. To wszystko znaczy właśnie, że automorfizmy ciała tworzą grupę: zbiór z odwracalnym działaniem (nazywanym zwyczajowo mnożeniem).
Grupa automorfizmów ciała będącego rozszerzeniem algebraicznym 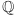 nie może być zbyt duża - liczba jej elementów nie przekracza stopnia rozszerzenia. Łatwo to wykazać, jeśli umiemy opisać rozszerzenie za pomocą jednego dodawanego elementu
nie może być zbyt duża - liczba jej elementów nie przekracza stopnia rozszerzenia. Łatwo to wykazać, jeśli umiemy opisać rozszerzenie za pomocą jednego dodawanego elementu 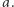 Co wtedy dzieje się z wielomianem minimalnym dla
Co wtedy dzieje się z wielomianem minimalnym dla 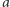 przy automorfizmie
przy automorfizmie 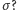 Nic! Jego współczynniki pochodzą z ciała zachowywanego przez
Nic! Jego współczynniki pochodzą z ciała zachowywanego przez 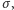 więc wielomian pozostaje bez zmian. A ponieważ
więc wielomian pozostaje bez zmian. A ponieważ  jest jego pierwiastkiem, więc
jest jego pierwiastkiem, więc 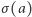 też musi być jego pierwiastkiem. Teraz wystarczy zauważyć, że wybór wartości
też musi być jego pierwiastkiem. Teraz wystarczy zauważyć, że wybór wartości 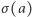 określa
określa 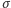 jednoznacznie, mamy więc co najwyżej tyle różnych automorfizmów, ile (różnych) pierwiastków wielomianu minimalnego.
jednoznacznie, mamy więc co najwyżej tyle różnych automorfizmów, ile (różnych) pierwiastków wielomianu minimalnego.
I wreszcie twierdzenia.
Galois interesował się specjalnym rodzajem automorfizmów ciał. Dla ustalonego rozszerzenia 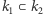 szukał takich automorfizmów ciała
szukał takich automorfizmów ciała 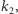 które trzymają w miejscu wszystkie elementy
które trzymają w miejscu wszystkie elementy 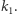 Tak wybrane automorfizmy też tworzą grupę, nazywaną grupą Galois rozszerzenia i oznaczaną
Tak wybrane automorfizmy też tworzą grupę, nazywaną grupą Galois rozszerzenia i oznaczaną 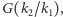 zwykle trochę mniejszą niż grupa wszystkich automorfizmów
zwykle trochę mniejszą niż grupa wszystkich automorfizmów 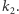 Badał też przejście w drugą stronę, od grupy do rozszerzenia ciał. Dla dowolnej podgrupy
Badał też przejście w drugą stronę, od grupy do rozszerzenia ciał. Dla dowolnej podgrupy 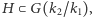 czyli mniejszej grupy zawartej w większej, można wyznaczyć zbiór wspólnych punktów stałych wszystkich automorfizmów
czyli mniejszej grupy zawartej w większej, można wyznaczyć zbiór wspólnych punktów stałych wszystkich automorfizmów 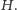 Okazuje się, że to też będzie ciało
Okazuje się, że to też będzie ciało 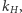 leżące gdzieś pomiędzy
leżące gdzieś pomiędzy 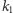 i
i 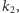 a więc tworzące z nimi wieżę rozszerzeń
a więc tworzące z nimi wieżę rozszerzeń 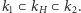
Powiemy, że rozszerzenie 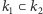 jest rozszerzeniem Galois, jeśli wykonanie kolejno obu tych operacji powoduje powrót do punktu wyjścia, czyli jeśli elementy ciała
jest rozszerzeniem Galois, jeśli wykonanie kolejno obu tych operacji powoduje powrót do punktu wyjścia, czyli jeśli elementy ciała 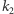 trzymane w miejscu przez każdy automorfizm z grupy
trzymane w miejscu przez każdy automorfizm z grupy 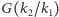 to dokładnie elementy ciała
to dokładnie elementy ciała 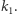 Główny wynik Galois to obserwacja, że rozszerzenia Galois zachowują się bardzo porządnie względem opisanych dwóch operacji. Na tyle porządnie, że, w pewnym zakresie, zamiast badać duże zbiory o złożonej strukturze - ciała i ich rozszerzenia - możemy odczytywać informacje ze struktury ich grup symetrii, zwykle znacznie prostszej. A dokładnie, opisane operacje brania grupy Galois rozszerzenia i brania ciała punktów stałych grupy automorfizmów zadają wzajemnie jednoznaczną odpowiedniość między ciałami
Główny wynik Galois to obserwacja, że rozszerzenia Galois zachowują się bardzo porządnie względem opisanych dwóch operacji. Na tyle porządnie, że, w pewnym zakresie, zamiast badać duże zbiory o złożonej strukturze - ciała i ich rozszerzenia - możemy odczytywać informacje ze struktury ich grup symetrii, zwykle znacznie prostszej. A dokładnie, opisane operacje brania grupy Galois rozszerzenia i brania ciała punktów stałych grupy automorfizmów zadają wzajemnie jednoznaczną odpowiedniość między ciałami 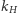 leżącymi w środku rozszerzenia Galois
leżącymi w środku rozszerzenia Galois 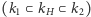 a podgrupami grupy Galois
a podgrupami grupy Galois 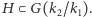 Co więcej, ta odpowiedniość pozwala sprawdzić, kiedy rozszerzenie
Co więcej, ta odpowiedniość pozwala sprawdzić, kiedy rozszerzenie 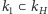 jest rozszerzeniem Galois (natomiast
jest rozszerzeniem Galois (natomiast 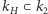 zawsze jest Galois). Dzieje się tak wtedy, gdy podgrupa
zawsze jest Galois). Dzieje się tak wtedy, gdy podgrupa 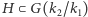 ma dobre własności: jest tak zwaną podgrupą normalną, czyli niezmienniczą ze względu na pewną klasę automorfizmów
ma dobre własności: jest tak zwaną podgrupą normalną, czyli niezmienniczą ze względu na pewną klasę automorfizmów 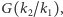 nazywanych sprzężeniami. Co ciekawe, pojęcie podgrupy normalnej pojawia się w bardzo wielu zagadnieniach algebraicznych, ale pierwszy raz zostało wyszczególnione właśnie przez Galois przy okazji powyższego twierdzenia.
nazywanych sprzężeniami. Co ciekawe, pojęcie podgrupy normalnej pojawia się w bardzo wielu zagadnieniach algebraicznych, ale pierwszy raz zostało wyszczególnione właśnie przez Galois przy okazji powyższego twierdzenia.
Jak to wygląda w praktyce?
Wróćmy do przykładu 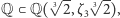 czyli ciała rozkładu
czyli ciała rozkładu 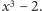 W naszej sytuacji, czyli przy założeniu, że wszystkie rozważane ciała zawierają
W naszej sytuacji, czyli przy założeniu, że wszystkie rozważane ciała zawierają 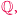 bycie ciałem rozkładu wystarcza do bycia rozszerzeniem Galois. Grupa Galois tego rozszerzenia ma 6 elementów, ponieważ dla rozszerzenia Galois liczba jej elementów musi być równa stopniowi rozszerzenia. Wiemy ponadto, że automorfizm z grupy Galois może przeprowadzać pierwiastki wielomianu o współczynnikach z
bycie ciałem rozkładu wystarcza do bycia rozszerzeniem Galois. Grupa Galois tego rozszerzenia ma 6 elementów, ponieważ dla rozszerzenia Galois liczba jej elementów musi być równa stopniowi rozszerzenia. Wiemy ponadto, że automorfizm z grupy Galois może przeprowadzać pierwiastki wielomianu o współczynnikach z 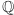 tylko na inne pierwiastki tego wielomianu, czyli je permutuje. Wielomian
tylko na inne pierwiastki tego wielomianu, czyli je permutuje. Wielomian 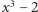 ma trzy różne pierwiastki, które można spermutować na 6 sposobów. Ponadto każda permutacja wyznacza już jednoznacznie automorfizm
ma trzy różne pierwiastki, które można spermutować na 6 sposobów. Ponadto każda permutacja wyznacza już jednoznacznie automorfizm 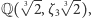 ponieważ mówi, jakie mają być obrazy generatorów tego rozszerzenia. Wobec tego grupa Galois
ponieważ mówi, jakie mają być obrazy generatorów tego rozszerzenia. Wobec tego grupa Galois 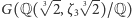 to grupa wszystkich permutacji trójelementowego zbioru!
to grupa wszystkich permutacji trójelementowego zbioru!
Ponadto można sprawdzić, na przykład badając własności permutacji, że jedyną (nietrywialną) normalną podgrupą jest grupa cyklicznych permutacji trzech elementów. A wewnątrz 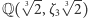 możemy znaleźć ciało
możemy znaleźć ciało 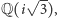 ponieważ
ponieważ

Okazuje się, że to dokładnie ciało punktów stałych podgrupy trójelementowych cykli, więc rozszerzenie 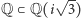 jest Galois - co zgadza się z faktem, że stanowi ono ciało rozkładu
jest Galois - co zgadza się z faktem, że stanowi ono ciało rozkładu 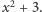
Jak to powiązać z klasyczną geometrią?
W przypadku konstrukcji geometrycznych kluczowym spostrzeżeniem jest to, że jeśli z pewnego zbioru punktów umiemy za pomocą cyrkla i linijki otrzymać nowy punkt, to jego współrzędne należą do rozszerzenia algebraicznego stopnia 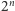 ciała zawierającego współrzędne danych punktów. Działanie cyrkla i linijki można opisać algebraicznie przez układy równań stopnia co najwyżej 2, więc każdy krok konstrukcji to rozszerzenie ciała o pierwiastek równania kwadratowego (lub brak rozszerzenia, jeśli nowe współrzędne już należą do ciała generowanego przez wcześniejsze). Wobec tego, jeśli mamy dany sześcian o boku długości 1, to konstrukcja sześcianu o dwukrotnie większej objętości wymagałaby umiejętności otrzymania odcinka o długości
ciała zawierającego współrzędne danych punktów. Działanie cyrkla i linijki można opisać algebraicznie przez układy równań stopnia co najwyżej 2, więc każdy krok konstrukcji to rozszerzenie ciała o pierwiastek równania kwadratowego (lub brak rozszerzenia, jeśli nowe współrzędne już należą do ciała generowanego przez wcześniejsze). Wobec tego, jeśli mamy dany sześcian o boku długości 1, to konstrukcja sześcianu o dwukrotnie większej objętości wymagałaby umiejętności otrzymania odcinka o długości 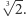 Ta liczba, jak wiemy, jest stopnia 3 nad
Ta liczba, jak wiemy, jest stopnia 3 nad 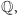 co nie pozwala jej znaleźć się w żadnym rozszerzeniu
co nie pozwala jej znaleźć się w żadnym rozszerzeniu 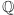 stopnia
stopnia 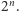
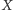 jest zamknięty ze względu na pewne działanie, jeśli wynik tego działania wykonanego na elementach
jest zamknięty ze względu na pewne działanie, jeśli wynik tego działania wykonanego na elementach 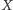 jest elementem
jest elementem 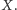 Na przykład zbiór
Na przykład zbiór 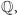 jak i każde inne ciało, jest zamknięty ze względu na dodawanie, odejmowanie, mnożenie i dzielenie przez niezerowe elementy. Natomiast zbiór liczb całkowitych nie jest zamknięty ze względu na dzielenie, więc nie jest ciałem.
jak i każde inne ciało, jest zamknięty ze względu na dodawanie, odejmowanie, mnożenie i dzielenie przez niezerowe elementy. Natomiast zbiór liczb całkowitych nie jest zamknięty ze względu na dzielenie, więc nie jest ciałem.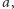 to biorąc ich różnicę, otrzymalibyśmy wielomian (niezerowy!) niższego stopnia, którego pierwiastkiem byłoby
to biorąc ich różnicę, otrzymalibyśmy wielomian (niezerowy!) niższego stopnia, którego pierwiastkiem byłoby 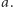 Czyli wcale nie zaczynalibyśmy od wielomianów minimalnych!
Czyli wcale nie zaczynalibyśmy od wielomianów minimalnych!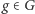 to automorfizm, który elementowi
to automorfizm, który elementowi 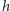 przyporządkowuje wynik mnożenia
przyporządkowuje wynik mnożenia 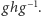 Wobec tego
Wobec tego 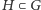 jest podgrupą normalną, jeśli dla dowolnych
jest podgrupą normalną, jeśli dla dowolnych 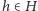 i
i 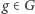 zachodzi
zachodzi 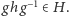
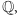 to twierdzenia Galois pozostają prawdziwe, a do niektórych omawianych po drodze wyników potrzebne jest założenie rozdzielczości rozszerzenia, co oznacza, że żaden wielomian rozkładalny w większym ciele nie może mieć w nim wielokrotnych pierwiastków.
to twierdzenia Galois pozostają prawdziwe, a do niektórych omawianych po drodze wyników potrzebne jest założenie rozdzielczości rozszerzenia, co oznacza, że żaden wielomian rozkładalny w większym ciele nie może mieć w nim wielokrotnych pierwiastków.