Combinatorial Nullstellensatz w teorii liczb
W Delcie 7/2017 przedstawiliśmy kilka "olimpijskich" zastosowań twierdzenia Combinatorial Nullstellensatz. Okazuje się, że zamiast "zwykłych" wielomianów wielu zmiennych możemy rozważać wielomiany o współczynnikach będących resztami z dzielenia przez pewną liczbę pierwszą 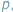 z dodawaniem i mnożeniem modulo
z dodawaniem i mnożeniem modulo 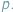 Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.
Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.

Twierdzenie Combinatorial Nullstellensatz można sformułować następująco:
Twierdzenie 5 (Combinatorial Nullstellensatz). Niech 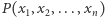 będzie niezerowym wielomianem
będzie niezerowym wielomianem  zmiennych stopnia
zmiennych stopnia 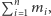 w którym współczynnik przy
w którym współczynnik przy 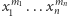 jest różny od zera. Wówczas dla dowolnych zbiorów
jest różny od zera. Wówczas dla dowolnych zbiorów 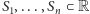 spełniających warunki
spełniających warunki 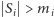 dla
dla 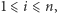 istnieją takie
istnieją takie 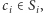 że
że 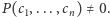
Okazuje się, że zamiast "zwykłych" wielomianów wielu zmiennych możemy rozważać wielomiany o współczynnikach będących resztami z dzielenia przez pewną liczbę pierwszą  z dodawaniem i mnożeniem modulo
z dodawaniem i mnożeniem modulo 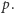 Zbiór tych reszt wraz z tak określonymi operacjami oznaczać będziemy jako
Zbiór tych reszt wraz z tak określonymi operacjami oznaczać będziemy jako  Dla
Dla 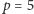 będziemy zatem mieli, na przykład,
będziemy zatem mieli, na przykład,

Twierdzenie 6 (Cauchy'ego-Davenporta). Dla dowolnej liczby pierwszej 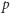 i dowolnych zbiorów
i dowolnych zbiorów 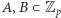 zachodzi nierówność
zachodzi nierówność

gdzie 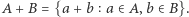
Dowód. Przyjmijmy najpierw, że 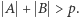 Niech
Niech  będzie dowolnym elementem zbioru
będzie dowolnym elementem zbioru 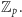 Zdefiniujmy dla elementu
Zdefiniujmy dla elementu  zbiór
zbiór 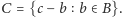 Zbiór
Zbiór  jest równoliczny ze zbiorem
jest równoliczny ze zbiorem 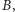 zatem
zatem 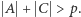 To oznacza, że istnieje element wspólny zbiorów
To oznacza, że istnieje element wspólny zbiorów 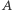 i
i  Niech elementem wspólnym będzie
Niech elementem wspólnym będzie 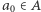 oraz
oraz  Wówczas
Wówczas  czyli
czyli 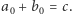 Wobec dowolności wyboru
Wobec dowolności wyboru  otrzymujemy, że
otrzymujemy, że 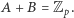
Załóżmy teraz, że 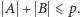 Dla dowodu nie wprost przypuśćmy, że
Dla dowodu nie wprost przypuśćmy, że  Wówczas w
Wówczas w  istnieje zbiór
istnieje zbiór 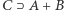 spełniający warunek
spełniający warunek 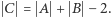 Rozważmy wielomian
Rozważmy wielomian

o współczynnikach z 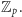 Jego stopień jest równy
Jego stopień jest równy 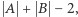 a współczynnik przy
a współczynnik przy 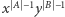 jest przystający do
jest przystający do 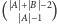 modulo
modulo  To wyrażenie nie jest podzielne przez
To wyrażenie nie jest podzielne przez 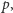 ponieważ
ponieważ 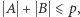 jest zatem (modulo
jest zatem (modulo 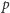 ) różne od 0. Na podstawie Combinatorial Nullstellensatz istnieją takie elementy
) różne od 0. Na podstawie Combinatorial Nullstellensatz istnieją takie elementy  że
że 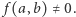 To jest niemożliwe, gdyż
To jest niemożliwe, gdyż 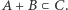 Zatem
Zatem 
Twierdzenie 7 (Erdősa-Heilbronna). Dla dowolnej liczby pierwszej 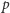 i dla dowolnego zbioru
i dla dowolnego zbioru 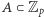 zachodzi nierówność:
zachodzi nierówność:

gdzie 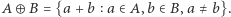
Dowód. Dla 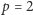 twierdzenie jest oczywiste. Załóżmy więc, że
twierdzenie jest oczywiste. Załóżmy więc, że  Niech
Niech  Wykażemy, że
Wykażemy, że 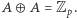 Wybierzmy dowolny element
Wybierzmy dowolny element 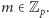 Rozbijmy zbiór
Rozbijmy zbiór  na pary elementów, których suma w
na pary elementów, których suma w 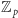 jest równa
jest równa 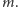 Otrzymujemy
Otrzymujemy 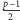 par oraz jeden element, który tworzy parę sam ze sobą. Wobec założenia
par oraz jeden element, który tworzy parę sam ze sobą. Wobec założenia  na podstawie zasady Dirichleta, do zbioru
na podstawie zasady Dirichleta, do zbioru 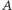 należą dwa różne elementy jednej z par, a więc
należą dwa różne elementy jednej z par, a więc 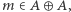 co należało dowieść. Niech teraz
co należało dowieść. Niech teraz  Wybierzmy dowolny element
Wybierzmy dowolny element  i zdefiniujmy
i zdefiniujmy 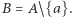 Łatwo zauważyć, że
Łatwo zauważyć, że 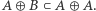 Potrzeba jeszcze pokazać, że
Potrzeba jeszcze pokazać, że  Wykażemy, że w tym przypadku
Wykażemy, że w tym przypadku 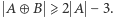 Dla dowodu nie wprost przyjmiemy, że istnieje taki podzbiór
Dla dowodu nie wprost przyjmiemy, że istnieje taki podzbiór  że
że 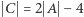 oraz
oraz 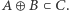 Rozważmy wielomian
Rozważmy wielomian

o współczynnikach z 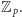 Jest to wielomian stopnia
Jest to wielomian stopnia 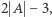 a współczynnik przy
a współczynnik przy 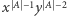 jest równy
jest równy
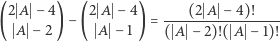 |
i jest różny od 0 w  gdyż
gdyż  Ponieważ zbiór
Ponieważ zbiór 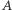 ma moc większą niż wykładnik
ma moc większą niż wykładnik 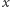 oraz
oraz 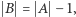 to z Combinatorial Nullstellensatz wynika, że istnieją takie elementy
to z Combinatorial Nullstellensatz wynika, że istnieją takie elementy 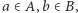 że
że 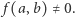 Otrzymaliśmy sprzeczność z własnością
Otrzymaliśmy sprzeczność z własnością 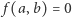 dla dowolnych
dla dowolnych 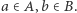
Twierdzenie 8 (Erdősa-Ginzburga-Ziva). Niech 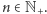 Wówczas wśród dowolnych
Wówczas wśród dowolnych 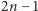 liczb całkowitych można wybrać
liczb całkowitych można wybrać 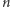 liczb, których suma jest podzielna przez
liczb, których suma jest podzielna przez 
Dowód. Najpierw wykażemy, że twierdzenie jest prawdziwe, jeśli 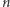 jest liczbą pierwszą; zgodnie z notacyjną tradycją przyjmijmy oznaczenie
jest liczbą pierwszą; zgodnie z notacyjną tradycją przyjmijmy oznaczenie 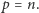 Niech
Niech 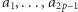 będą danymi liczbami całkowitymi. Bez straty ogólności można założyć, że
będą danymi liczbami całkowitymi. Bez straty ogólności można założyć, że 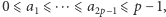 gdyż możemy rozważyć tylko reszty z dzielenia liczb
gdyż możemy rozważyć tylko reszty z dzielenia liczb 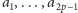 przez
przez 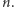 Rozważmy dwa przypadki.
Rozważmy dwa przypadki.
Przypadek 1. Jeżeli  dla pewnego
dla pewnego  to twierdzenie jest oczywiste: wybieramy liczby
to twierdzenie jest oczywiste: wybieramy liczby 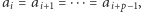 których suma jest podzielna przez
których suma jest podzielna przez 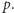
Przypadek 2. Niech 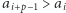 dla dowolnej liczby
dla dowolnej liczby 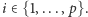 W tym przypadku rozważmy dwuelementowe zbiory
W tym przypadku rozważmy dwuelementowe zbiory

oraz zbiór jednoelementowy 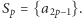 Zdefiniujmy wielomian
Zdefiniujmy wielomian

Wielomian 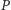 jest stopnia
jest stopnia 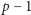 i współczynnik przy jednomianie
i współczynnik przy jednomianie 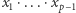 jest równy
jest równy 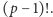 Nie jest on równy
Nie jest on równy 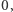 gdyż na podstawie twierdzenia Wilsona
gdyż na podstawie twierdzenia Wilsona 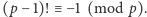 Na podstawie Combinatorial Nullstellensatz istnieje taki element
Na podstawie Combinatorial Nullstellensatz istnieje taki element  że
że 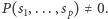 Gdyby suma
Gdyby suma 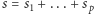 nie była podzielna przez
nie była podzielna przez 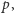 to na podstawie Małego Twierdzenia Fermata
to na podstawie Małego Twierdzenia Fermata  byłoby dzielnikiem
byłoby dzielnikiem 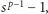 co nie jest prawdą, gdyż
co nie jest prawdą, gdyż 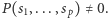 Wobec tego suma
Wobec tego suma 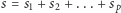 jest podzielna przez
jest podzielna przez 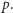

Teraz wykażemy, że twierdzenie jest prawdziwe dla dowolnej dodatniej liczby naturalnej 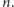 Każda liczba naturalna
Każda liczba naturalna 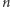 ma jednoznaczny rozkład, z dokładnością do kolejności, na iloczyn liczb pierwszych. Udowodniliśmy twierdzenie dla każdej liczby pierwszej. Zatem wystarczy wykazać, że twierdzenie jest prawdziwe dla dowolnego iloczynu liczb pierwszych. Wobec tego wystarczy wykazać, że jeżeli twierdzenie jest prawdziwe dla dwóch liczb naturalnych
ma jednoznaczny rozkład, z dokładnością do kolejności, na iloczyn liczb pierwszych. Udowodniliśmy twierdzenie dla każdej liczby pierwszej. Zatem wystarczy wykazać, że twierdzenie jest prawdziwe dla dowolnego iloczynu liczb pierwszych. Wobec tego wystarczy wykazać, że jeżeli twierdzenie jest prawdziwe dla dwóch liczb naturalnych 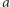 i
i 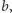 to jest prawdziwe dla ich iloczynu
to jest prawdziwe dla ich iloczynu 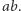
Załóżmy, że twierdzenie jest prawdziwe dla dwóch dodatnich liczb naturalnych 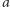 i
i 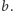 Wykażemy, że jest także prawdziwe dla ich iloczynu
Wykażemy, że jest także prawdziwe dla ich iloczynu 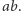 Spośród
Spośród 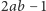 liczb wybierzmy
liczb wybierzmy 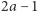 liczb. Spośród nich można wybrać
liczb. Spośród nich można wybrać 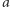 liczb, których suma jest podzielna przez
liczb, których suma jest podzielna przez 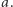 Zatem pozostaje
Zatem pozostaje  liczb. Ponownie wybierzmy
liczb. Ponownie wybierzmy 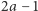 spośród nich. Wśród nich jest
spośród nich. Wśród nich jest  liczb, których suma jest podzielna przez
liczb, których suma jest podzielna przez 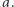 Pozostaje
Pozostaje 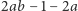 liczb. Postępujemy analogicznie
liczb. Postępujemy analogicznie 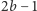 razy. Otrzymujemy w ten sposób
razy. Otrzymujemy w ten sposób 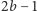 zbiorów, z których każdy zawiera
zbiorów, z których każdy zawiera 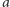 elementów, a suma tych elementów w każdym z tych zbiorów jest podzielna przez
elementów, a suma tych elementów w każdym z tych zbiorów jest podzielna przez 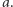 Potraktujmy sumę wybranych elementów każdego z tych zbiorów jako jedną liczbę i podzielmy ją przez
Potraktujmy sumę wybranych elementów każdego z tych zbiorów jako jedną liczbę i podzielmy ją przez 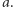 Otrzymujemy
Otrzymujemy 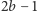 liczb, spośród których możemy wybrać
liczb, spośród których możemy wybrać 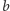 liczb, których suma jest podzielna przez
liczb, których suma jest podzielna przez  Zatem uzyskaliśmy
Zatem uzyskaliśmy 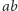 liczb, których suma jest podzielna przez
liczb, których suma jest podzielna przez 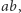 co kończy dowód twierdzenia, jak również cały artykuł.
co kończy dowód twierdzenia, jak również cały artykuł.