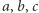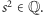Najłatwiejsze zadanie?
Na drugim etapie tegorocznej Olimpiady Matematycznej pojawiło się pewne zadanie. Pojawiło się ono na zawodach z numerem 1 i (zgodnie z oczekiwaniami) okazało się bardzo łatwe - rozwiązała je znacząca większość uczestników. Przedstawimy szkic rozwiązania... x
Zadanie 1. We wnętrzu trójkąta o bokach długości 3, 4, 5 leży punkt 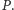 Wykazać, że jeżeli odległości
Wykazać, że jeżeli odległości 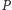 od wierzchołków są wszystkie wymierne, to odległości
od wierzchołków są wszystkie wymierne, to odległości 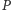 od boków też.
od boków też.
Szkic rozwiązania. Umieśćmy trójkąt (który jest, oczywiście, prostokątny) w układzie współrzędnych tak, by jego wierzchołkami były 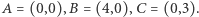 Niech punkt
Niech punkt 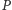 ma współrzędne
ma współrzędne 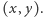 Wtedy z twierdzenia Pitagorasa wynika, że
Wtedy z twierdzenia Pitagorasa wynika, że 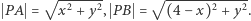 Stąd
Stąd
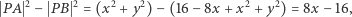
a ponieważ 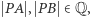 to
to 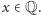 Analogicznie
Analogicznie 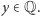 Zatem wykazaliśmy, że punkt
Zatem wykazaliśmy, że punkt 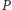 leży w wymiernych odległościach od boków
leży w wymiernych odległościach od boków 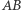 i
i 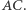 Odległość od boku
Odległość od boku 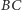 możemy obliczyć, korzystając, na przykład, ze wzoru na odległość punktu od prostej. Ponieważ prosta
możemy obliczyć, korzystając, na przykład, ze wzoru na odległość punktu od prostej. Ponieważ prosta 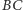 jest opisana równaniem
jest opisana równaniem 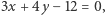 to szukana odległość wynosi
to szukana odległość wynosi
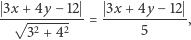
czyli jest wymierna.
Pomimo niewielkiej trudności samego zadania możemy powiązać z nim kilka ciekawych problemów. Pierwsze pytanie, które się nasuwa, brzmi: czy w ogóle istnieje punkt spełniający warunki zadania? Przed przejściem do dalszej części artykułu Czytelnik może sam spróbować poszukać takich punktów.
Chociaż ich ręczne znalezienie może być trudne, z pomocą komputera szybko znajdujemy kilka punktów spełniających nasze warunki. Najprostszy z nich (o najmniejszych mianownikach) ma współrzędne 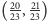 i jest odległy od wierzchołków
i jest odległy od wierzchołków 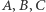 odpowiednio o
odpowiednio o 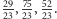
Tak naprawdę powiedzieć możemy dużo więcej. J.H.J. Almering w 1963 roku udowodnił, że
Dla dowolnego (niekoniecznie prostokątnego) trójkąta o bokach wymiernej długości zbiór punktów, których odległości od wszystkich wierzchołków są wymierne, nie tylko jest niepusty, ale nawet nieskończony i ponadto jest gęstym podzbiorem płaszczyzny!
Jak dowodzi T.G. Berry w pracy z 1992 roku, wystarczy jedynie założyć, że kwadraty długości boków są wymierne i co najmniej jeden bok trójkąta ma długość wymierną - to ostatnie założenie jest konieczne, bo w trójkącie o bokach 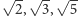 nie ma żadnego punktu o wymiernych odległościach od wierzchołków (zachęcamy Czytelnika do samodzielnego udowodnienia tego faktu).
nie ma żadnego punktu o wymiernych odległościach od wierzchołków (zachęcamy Czytelnika do samodzielnego udowodnienia tego faktu).
Kolejne pytanie, jakie możemy sobie postawić, dotyczy uogólnienia wyjściowego zadania. Rozumowanie analogiczne do przedstawionego powyżej rozwiązania pokazuje, że teza zadania jest spełniona dla dowolnego trójkąta prostokątnego o bokach wymiernych.
Wykażemy teraz, że teza zachodzi dla dowolnego trójkąta o bokach długości wymiernej i wymiernym polu. Zacznijmy od prostego lematu.
Lemat 1. Załóżmy, że trójkąt 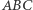 ma wymierne boki. Niech
ma wymierne boki. Niech 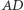 będzie wysokością tego trójkąta. Wtedy odcinki
będzie wysokością tego trójkąta. Wtedy odcinki 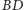 i
i 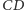 mają długości wymierne.
mają długości wymierne.
Dowód. Wiemy, że 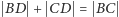 lub
lub 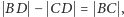 co jest liczbą wymierną. Ponadto z twierdzenia Pitagorasa wynika, że
co jest liczbą wymierną. Ponadto z twierdzenia Pitagorasa wynika, że 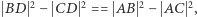 co też jest wymierne. Stąd
co też jest wymierne. Stąd 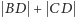 i
i 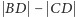 są wymierne, co natychmiast implikuje tezę lematu.
są wymierne, co natychmiast implikuje tezę lematu.
Załóżmy teraz, że trójkąt 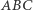 ma wymierne boki i wymierne pole. Przyjmując oznaczenia jak w lemacie, dostajemy, że
ma wymierne boki i wymierne pole. Przyjmując oznaczenia jak w lemacie, dostajemy, że 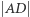 jest wymierne (ze wzoru na pole trójkąta), a także
jest wymierne (ze wzoru na pole trójkąta), a także 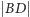 i
i 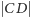 są wymierne. Zatem możemy ustawić trójkąt w układzie współrzędnych tak, aby punkty
są wymierne. Zatem możemy ustawić trójkąt w układzie współrzędnych tak, aby punkty 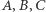 miały odpowiednio współrzędne
miały odpowiednio współrzędne 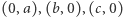 dla pewnych liczb wymiernych
dla pewnych liczb wymiernych 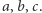 Rozważmy punkt
Rozważmy punkt 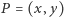 o wymiernych odległościach od punktów
o wymiernych odległościach od punktów 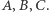 Kwadraty tych odległości też są liczbami wymiernymi i są równe odpowiednio
Kwadraty tych odległości też są liczbami wymiernymi i są równe odpowiednio 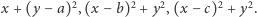 Czytelnik zechce samodzielnie sprawdzić, że wymierność tych liczb implikuje wymierność
Czytelnik zechce samodzielnie sprawdzić, że wymierność tych liczb implikuje wymierność 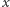 i
i 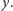
Możemy pójść jeszcze dalej i zapytać, czy da się uogólnić ten rezultat na inne wielokąty. Okazuje się, że tak:
Twierdzenie. Załóżmy, że 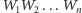 jest wielokątem wypukłym o wymiernych bokach
jest wielokątem wypukłym o wymiernych bokach 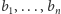 i wymiernym polu
i wymiernym polu 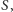 a
a 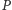 niech będzie punktem we wnętrzu tego wielokąta. Wówczas, jeśli wszystkie odległości
niech będzie punktem we wnętrzu tego wielokąta. Wówczas, jeśli wszystkie odległości 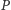 od wierzchołków tego wielokąta są wymierne, to również wszystkie odległości
od wierzchołków tego wielokąta są wymierne, to również wszystkie odległości 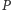 od jego boków są wymierne.
od jego boków są wymierne.
Dowód korzysta z następującego prostego faktu.
Wynika to, na przykład, ze słynnego wzoru Herona

ale można udowodnić to dużo prościej. Następny lemat jest bardziej wyrafinowany, ale przy naszym podejściu niezbędny.
Lemat 3. Załóżmy, że liczby 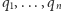 są wymierne i dodatnie oraz że liczba
są wymierne i dodatnie oraz że liczba 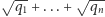 też jest wymierna. Wówczas wszystkie liczby
też jest wymierna. Wówczas wszystkie liczby 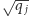 są wymierne.
są wymierne.
Czytelnik Oblatany może zgłębić zakamarki dowodu, a Czytelnik Nieśmiały na ten czas może przyjąć jego poprawność na wiarę i przejść do dalszej części.
Dowód. Załóżmy, że jest inaczej i rozważmy ciało 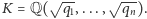 Mamy więc
Mamy więc 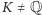 i ciało
i ciało 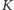 jest rozszerzeniem Galois ciała
jest rozszerzeniem Galois ciała 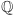 (gdyż jest ciałem rozkładu wielomianu
(gdyż jest ciałem rozkładu wielomianu 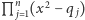 ). Niech
). Niech 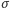 będzie dowolnym nietrywialnym automorfizmem
będzie dowolnym nietrywialnym automorfizmem 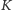 nad
nad 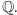 Ponieważ
Ponieważ
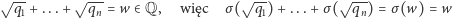
(gdyż 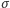 zachowuje działania). Dla każdego
zachowuje działania). Dla każdego 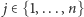 mamy
mamy 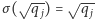 albo
albo 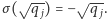 Ale z powyższych dwóch równości wynika, że zawsze musi być
Ale z powyższych dwóch równości wynika, że zawsze musi być 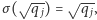 a zatem
a zatem 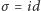 - sprzeczność.
- sprzeczność.
Przechodzimy teraz do dowodu uogólnienia. Niech 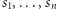 będą polami trójkątów
będą polami trójkątów 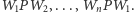 Z lematu 2 mamy
Z lematu 2 mamy 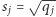 gdzie
gdzie 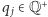 dla
dla 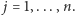 Z założenia
Z założenia 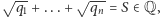 a zatem na podstawie lematu 3 mamy
a zatem na podstawie lematu 3 mamy 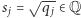 dla
dla 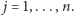 Z wymierności boków wielokąta i wzoru na pole trójkąta wynika teraz, że odległości punktu
Z wymierności boków wielokąta i wzoru na pole trójkąta wynika teraz, że odległości punktu 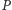 od boków są wymierne.
od boków są wymierne.