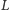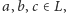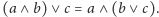O pewnych kratach testowych
Teoria krat pojawiła się pod koniec XIX wieku, wyrastając z logiki i algebry. W logice kraty pojawiły się za sprawą George’a Boole’a, a w algebrze kraty pierwszy rozpatrywał Richard Dedekind. Kraty są przedmiotem badań algebraików, stanowią jednocześnie wygodny środek opisu znanych struktur matematycznych, których przykłady przedstawię w dalszej części artykułu.

Kraty można opisać na dwa sposoby: algebraicznie lub przy użyciu częściowych porządków.
Definicja 1. Krata w sensie algebraicznym to struktura algebraiczna
 spełniająca dla dowolnych elementów
spełniająca dla dowolnych elementów
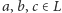 następujące
równości:
następujące
równości:

Krata w sensie częściowych porządków to niepusty częściowo uporządkowany
zbiór
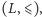 w którym każdy dwuelementowy podzbiór ma oba kresy:
górny i dolny.
w którym każdy dwuelementowy podzbiór ma oba kresy:
górny i dolny.
Pojęcia krat w sensie algebraicznym i częściowych porządków są równoważne.
Jeśli zdefiniujemy kratę jako zbiór algebraiczny z wymienionymi aksjomatami,
to zadając porządek przez
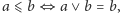 otrzymamy kratę w sensie
porządku. Odwrotnie, jeśli w kracie w sensie porządku zdefiniujemy
otrzymamy kratę w sensie
porządku. Odwrotnie, jeśli w kracie w sensie porządku zdefiniujemy
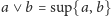 oraz
oraz
 to dostaniemy kratę
w sensie algebraicznym.
to dostaniemy kratę
w sensie algebraicznym.
Zanim omówię wybrane przykłady krat, podam kilka użytecznych definicji.
Kratę
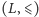 będziemy zwykle oznaczali literą
będziemy zwykle oznaczali literą
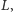 identyfikując ją ze
zbiorem jej elementów. Jeśli w kracie
identyfikując ją ze
zbiorem jej elementów. Jeśli w kracie
 istnieje element największy, to
nazywamy go jednością kraty i oznaczamy przez
istnieje element największy, to
nazywamy go jednością kraty i oznaczamy przez
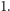 Podobnie, najmniejszy
element w kracie (jeśli istnieje) oznaczamy symbolem 0 i nazywamy zerem
kraty. Kratę z zerem i jednością nazywamy kratą ograniczoną. Podzbiór
Podobnie, najmniejszy
element w kracie (jeśli istnieje) oznaczamy symbolem 0 i nazywamy zerem
kraty. Kratę z zerem i jednością nazywamy kratą ograniczoną. Podzbiór
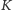 kraty
kraty
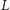 nazwiemy jej podkratą, jeśli dla dowolnych
nazwiemy jej podkratą, jeśli dla dowolnych
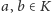 mamy
mamy
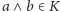 oraz
oraz
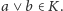 Powiemy, że kraty
Powiemy, że kraty
 i
i
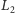 są izomorficzne wtedy i tylko wtedy, gdy istnieje bijekcja
są izomorficzne wtedy i tylko wtedy, gdy istnieje bijekcja
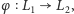 taka że
taka że
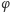 i
i
 zachowują porządek, tj.
zachowują porządek, tj.

Zauważmy, że jeśli
 jest kratą, to para
jest kratą, to para
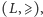 gdzie
relacja
gdzie
relacja
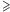 zdefiniowana jest wzorem
zdefiniowana jest wzorem
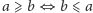 również
jest kratą. Kratę
również
jest kratą. Kratę
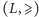 będziemy nazywać kratą dualną do kraty
będziemy nazywać kratą dualną do kraty
 i oznaczać symbolem
i oznaczać symbolem
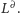 Łatwo sprawdzić, że jeśli
Łatwo sprawdzić, że jeśli
 w kracie
w kracie
 to
to
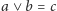 w kracie
w kracie
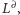 oraz
analogicznie jeśli
oraz
analogicznie jeśli
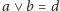 w kracie
w kracie
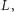 to
to
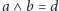 w kracie
w kracie
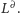
Przykład 1.
Niech
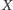 będzie dowolnym zbiorem. Rodzina
będzie dowolnym zbiorem. Rodzina
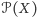 wszystkich
podzbiorów zbioru
wszystkich
podzbiorów zbioru
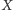 wraz
z porządkiem zadanym przez inkluzję
wraz
z porządkiem zadanym przez inkluzję
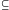 jest kratą. Mianowicie, jeśli
jest kratą. Mianowicie, jeśli
 to
to
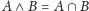 oraz
oraz
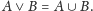 Jest
to krata ograniczona. Zerem tej kraty jest zbiór pusty, a jednością zbiór
Jest
to krata ograniczona. Zerem tej kraty jest zbiór pusty, a jednością zbiór
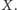
Przykład 2. Niech
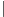 oznacza
relację podzielności w zbiorze
oznacza
relację podzielności w zbiorze
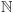 dodatnich liczb całkowitych. Niech
dodatnich liczb całkowitych. Niech
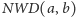 tradycyjnie oznacza największy wspólny
dzielnik liczb
tradycyjnie oznacza największy wspólny
dzielnik liczb
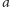 i
i
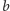 oraz
oraz
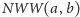 ich najmniejszą
wspólną wielokrotność. Zbiór uporządkowany
ich najmniejszą
wspólną wielokrotność. Zbiór uporządkowany
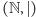 jest kratą
z działaniami
jest kratą
z działaniami
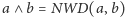 oraz
oraz
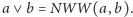 Krata ta ma
element najmniejszy równy
Krata ta ma
element najmniejszy równy
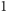 i nie ma elementu największego.
i nie ma elementu największego.
Przykład 3. Niech
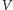 będzie
przestrzenią liniową nad ciałem
będzie
przestrzenią liniową nad ciałem
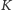 i niech
i niech
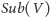 oznacza
rodzinę wszystkich jej podprzestrzeni. Zbiór
oznacza
rodzinę wszystkich jej podprzestrzeni. Zbiór
 jest kratą.
Jeśli
jest kratą.
Jeśli
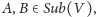 to
to
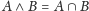 oraz
oraz
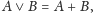 gdzie
gdzie
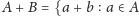 i
i
 Zerem w tej kracie jest wektor
zerowy, a jedynką cała przestrzeń
Zerem w tej kracie jest wektor
zerowy, a jedynką cała przestrzeń
 Podobnie, kratami są również: rodzina podgrup zadanej grupy,
rodzina jej dzielników normalnych oraz rodzina podpierścieni danego
pierścienia, wszystko z relacją inkluzji.
Podobnie, kratami są również: rodzina podgrup zadanej grupy,
rodzina jej dzielników normalnych oraz rodzina podpierścieni danego
pierścienia, wszystko z relacją inkluzji.
Przykład 4.
Niech
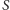 będzie rodziną podzbiorów przestrzeni
będzie rodziną podzbiorów przestrzeni
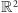 złożoną
ze zbioru pustego, całej przestrzeni
złożoną
ze zbioru pustego, całej przestrzeni
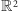 oraz wszystkich punktów
i wszystkich prostych w
oraz wszystkich punktów
i wszystkich prostych w
 Zbiór ten z relacją zawierania stanowi
kratę ograniczoną. Zerem tej kraty jest zbiór pusty, a jednością
Zbiór ten z relacją zawierania stanowi
kratę ograniczoną. Zerem tej kraty jest zbiór pusty, a jednością
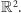
Kraty, tak jak wszystkie porządki, możemy ilustrować za pomocą diagramów,
które tworzymy w następujący sposób: elementy kraty
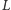 zaznaczamy na
płaszczyźnie jako punkty. Jeśli
zaznaczamy na
płaszczyźnie jako punkty. Jeśli
 są elementami kraty
są elementami kraty
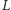 oraz
oraz
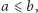 to punkt odpowiadający elementowi
to punkt odpowiadający elementowi
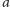 rysujemy
poniżej punktu odpowiadającego elementowi
rysujemy
poniżej punktu odpowiadającego elementowi
 Jeśli
Jeśli
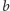 jest
następnikiem
jest
następnikiem
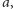 czyli
czyli
 oraz nie istnieje
oraz nie istnieje
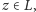 taki że
taki że
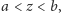 to punkty
to punkty
 i
i
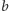 łączymy odcinkiem.
łączymy odcinkiem.

Rys. 1 Diagramy nieprzedstawiające krat.

Rys. 2 Kraty o co najwyżej trzech elementach.
Przyjrzyjmy się diagramom z rysunku 1. Widzimy, że na diagramie (a)
elementy
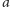 i
i
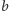 nie mają kresu górnego, a w przypadku
diagramu (b) elementy
nie mają kresu górnego, a w przypadku
diagramu (b) elementy
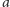 i
i
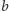 nie mają kresu dolnego. Na
diagramie (c) elementy
nie mają kresu dolnego. Na
diagramie (c) elementy
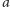 i
i
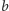 mają dwa ograniczenia górne
mają dwa ograniczenia górne
 i
i
 ale nie mają kresu górnego. Zatem diagramy te nie
przedstawiają krat.
ale nie mają kresu górnego. Zatem diagramy te nie
przedstawiają krat.
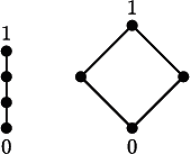
Wskażemy teraz diagramy porządków będących kratami. Oczywiście, każdy liniowo uporządkowany zbiór (często nazywany łańcuchem) jest kratą. Łatwo można sprawdzić, że kraty o co najwyżej trzech elementach muszą być łańcuchami.
Rys. 3 Kraty czteroelementowe.

Rys. 4 Kraty pięcioelementowe.
Kraty o czterech elementach są tylko dwie (z dokładnością do izomorfizmu), a krat pięcioelementowych jest dokładnie pięć (Rys. 3 i 4).
W matematyce ważną rolę spełniają kraty rozdzielne i modularne.
Definicja 3. Kratę
 nazywamy rozdzielną (dystrybutywną), gdy
dla dowolnych jej elementów
nazywamy rozdzielną (dystrybutywną), gdy
dla dowolnych jej elementów
 spełniona jest równość
spełniona jest równość

Wprost z definicji wynika, iż każda krata rozdzielna jest modularna.
Zwróćmy uwagę, że wszystkie łańcuchy są kratami rozdzielnymi. Rozważmy
kratę z przykładu 1 – równość z definicji kraty rozdzielnej w przypadku
kraty
 ma postać dobrze znanego prawa rozdzielności przecięcia
zbiorów względem dodawania
ma postać dobrze znanego prawa rozdzielności przecięcia
zbiorów względem dodawania
 zatem
krata
zatem
krata
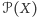 jest rozdzielna. W tym przypadku nie napotkaliśmy
problemów z wykazaniem tej własności, często jednak sprawdzenie wprost
z definicji, czy dana krata jest dystrybutywna bądź modularna, jest dość
kłopotliwe. Na szczęście istnieją niezwykle obrazowe i przydatne twierdzenia
sprowadzające problem do pytania, czy wśród jej podkrat znajdują się pewne
wymienione wcześniej kraty.
jest rozdzielna. W tym przypadku nie napotkaliśmy
problemów z wykazaniem tej własności, często jednak sprawdzenie wprost
z definicji, czy dana krata jest dystrybutywna bądź modularna, jest dość
kłopotliwe. Na szczęście istnieją niezwykle obrazowe i przydatne twierdzenia
sprowadzające problem do pytania, czy wśród jej podkrat znajdują się pewne
wymienione wcześniej kraty.
Twierdzenie 1. Krata
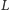 jest modularna wtedy i tylko wtedy, gdy nie
ma podkraty izomorficznej z
jest modularna wtedy i tylko wtedy, gdy nie
ma podkraty izomorficznej z
 (Rys. 4).
(Rys. 4).
Szkic dowodu. Łatwo zauważyć, że jeśli
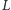 ma podkratę
izomorficzną z
ma podkratę
izomorficzną z
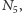 to nie jest modularna. Załóżmy teraz, że
to nie jest modularna. Załóżmy teraz, że
 nie jest modularna, tzn. istnieją
nie jest modularna, tzn. istnieją
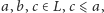 takie że
takie że
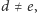 gdzie
gdzie
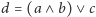 i
i
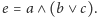 Z założenia
Z założenia
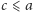 oraz oczywistych relacji
oraz oczywistych relacji
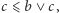
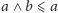 i
i
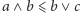 w prosty sposób
wynika
w prosty sposób
wynika
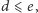 więc
więc
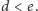 Wykażemy, że
Wykażemy, że
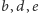 wraz z
wraz z
 i
i
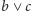 tworzą kratę izomorficzną
z
tworzą kratę izomorficzną
z
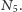 Najpierw upewnimy się, że
Najpierw upewnimy się, że
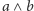 i
i
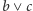 są
różne od reszty wyszczególnionych elementów – istotnie, gdyby
było
są
różne od reszty wyszczególnionych elementów – istotnie, gdyby
było
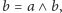 to mielibyśmy
to mielibyśmy
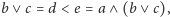 co
jest niemożliwe; podobnie dowodzimy, że
co
jest niemożliwe; podobnie dowodzimy, że
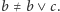 Ponadto
Ponadto
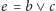 byłoby równoznaczne z
byłoby równoznaczne z
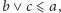 skąd
skąd
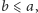 czyli
czyli
 co jak już wiemy,
jest niemożliwe; analogicznie
co jak już wiemy,
jest niemożliwe; analogicznie
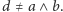 Korzystając z własności
działań kratowych, otrzymujemy
Korzystając z własności
działań kratowych, otrzymujemy

i analogicznie
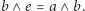 Ponadto, skoro zachodzi
Ponadto, skoro zachodzi
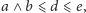 to
to

tak
więc
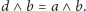 Podobnie dowodzimy
Podobnie dowodzimy
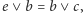 co
w połączeniu z wykazanymi wcześniej zależnościami prowadzi nas
już do wniosku, że wskazane elementy faktycznie tworzą podkratę
izomorficzną z
co
w połączeniu z wykazanymi wcześniej zależnościami prowadzi nas
już do wniosku, że wskazane elementy faktycznie tworzą podkratę
izomorficzną z
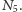
W analogiczny, choć nieco bardziej skomplikowany sposób, otrzymujemy podobny wynik dla krat rozdzielnych.
Twierdzenie 2. Krata
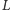 jest rozdzielna wtedy i tylko wtedy, gdy nie
ma podkraty izomorficznej z
jest rozdzielna wtedy i tylko wtedy, gdy nie
ma podkraty izomorficznej z
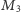 lub
lub
 (patrz Rys. 4).
(patrz Rys. 4).
Z podanych twierdzeń w prosty sposób wynika, że jeśli krata
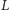 jest modularna (rozdzielna), to krata
jest modularna (rozdzielna), to krata
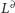 również jest
modularna (rozdzielna).
również jest
modularna (rozdzielna).

Weźmy teraz kratę z przykładu 3. Gdyby
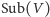 nie była modularna, to
w kracie tej istniałaby podkrata izomorficzna z
nie była modularna, to
w kracie tej istniałaby podkrata izomorficzna z
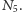 Istniałyby zatem
parami różne podprzestrzenie
Istniałyby zatem
parami różne podprzestrzenie
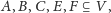 takie że
takie że
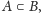
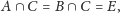 oraz
oraz
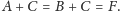 Nie jest to jednak
możliwe, co pozostawiam Czytelnikowi Podejrzliwemu jako nietrudne zadanie
z algebry liniowej. Krata
Nie jest to jednak
możliwe, co pozostawiam Czytelnikowi Podejrzliwemu jako nietrudne zadanie
z algebry liniowej. Krata
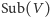 jest zatem kratą modularną,
jednocześnie łatwo wykazać, że nie jest to krata rozdzielna. Weźmy
przestrzeń
jest zatem kratą modularną,
jednocześnie łatwo wykazać, że nie jest to krata rozdzielna. Weźmy
przestrzeń
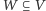 wymiaru dwa i trzy jej różne jednowymiarowe
podprzestrzenie
wymiaru dwa i trzy jej różne jednowymiarowe
podprzestrzenie
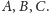 Podprzestrzenie
Podprzestrzenie
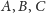 przecinają się
w wektorze zerowym i każde dwie z nich generują
przecinają się
w wektorze zerowym i każde dwie z nich generują
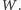 Dostajemy
zatem podkratę izomorficzną z
Dostajemy
zatem podkratę izomorficzną z
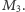
Wykażemy teraz, że krata z przykładu 4 nie jest nawet modularna. Zauważmy,
że jeżeli
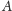 oznacza punkt leżący na prostej
oznacza punkt leżący na prostej
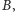 a przez
a przez
 oznaczymy prostą nieprzecinającą prostej
oznaczymy prostą nieprzecinającą prostej
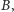 to otrzymujemy
podkratę:
to otrzymujemy
podkratę:
Kraty modularne i rozdzielne są dokładnie opisane w literaturze i znamy wiele
ich własności. Poza nimi rozważa się, oczywiście, wiele innych rodzajów
tych struktur. Niektóre z nich dają się scharakteryzować poprzez zawieranie
pewnej podkraty lub podkrat. Te charakterystyczne obiekty (np.
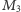 oraz
oraz
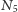 ) to właśnie tytułowe kraty testowe.
) to właśnie tytułowe kraty testowe.