Kolorowanie wielomianów
Za pomocą kolorowania wielomianów można udowodnić Zasadnicze twierdzenie algebry w zaskakująco elementarny sposób...
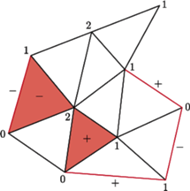
Rys. 1 Striangulowany wielokąt; kolorem wyróżniono trójkąty i odcinki odgrywające rolę w lemacie Spernera.
Lemat Spernera
Narysujmy na płaszczyźnie wielokąt i dokonajmy jego triangulacji, czyli
podziału na trójkąty, które mogą stykać się z innymi trójkątami wspólną
krawędzią lub wspólnym wierzchołkiem (jak na rysunku 1). Wierzchołki tych
trójkątów „pokolorujemy”, tzn. każdemu z nich przypiszemy jego „kolor” –
liczbę ze zbioru
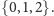
Wyróżnijmy trójkąty, które mają wierzchołki wszystkich trzech kolorów.
Jeśli poruszając się po obwodzie trójkąta przeciwnie do ruchu wskazówek
zegara widzimy liczby w kolejności 0, 1, 2, to mamy do czynienia z trójkątem
„dodatnio zorientowanym”. Oznaczmy liczbę takich trójkątów przez
 natomiast liczbę trójkątów „ujemnie zorientowanych” przez
natomiast liczbę trójkątów „ujemnie zorientowanych” przez
Interesować nas też będą krawędzie na brzegu wielokąta. Jeżeli wierzchołki
takiej krawędzi mają kolory
 i
i
 (przy czym kolor
(przy czym kolor
 ma
wierzchołek, który napotykamy najpierw, gdy poruszamy się po obwodzie
wielokąta przeciwnie do ruchu wskazówek zegara), to taką krawędź
nazwiemy
ma
wierzchołek, który napotykamy najpierw, gdy poruszamy się po obwodzie
wielokąta przeciwnie do ruchu wskazówek zegara), to taką krawędź
nazwiemy
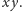 Wyróżnimy krawędzie, które mają kolory 0 i 1.
Krawędzie 01 nazwiemy „dodatnio zorientowanymi”, natomiast krawędzie
10 będą „ujemnie zorientowane”. Ich liczbę oznaczymy, odpowiednio, przez
Wyróżnimy krawędzie, które mają kolory 0 i 1.
Krawędzie 01 nazwiemy „dodatnio zorientowanymi”, natomiast krawędzie
10 będą „ujemnie zorientowane”. Ich liczbę oznaczymy, odpowiednio, przez
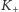 i
i
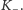
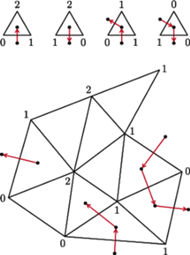
Rys. 2 Ilustracja dowodu lematu Spernera.
Ciekawy lemat (znany jako skierowana wersja lematu Spernera) podaje zależność między tym, co musi się dziać wewnątrz takiego striangulowanego wielokąta, a tym, co się dzieje na jego brzegu – mianowicie
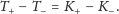 | (*) |
Dowód. Dowód lematu jest bardzo prosty. Przetnijmy każdą
z krawędzi 01 i 10 prostopadłym wektorem (w kierunku takim, jak na
rysunku 2) i utwórzmy z tych wektorów graf. Graf ten składa się
ze skierowanych ścieżek. Każda ścieżka zaczyna się w ujemnie
zorientowanym
trójkącie lub na dodatnio zorientowanym odcinku, natomiast kończy
się w dodatnio zorientowanym trójkącie lub na ujemnie zorientowanym
odcinku. Liczba początków
 musi być równa liczbie
końców ścieżek
musi być równa liczbie
końców ścieżek
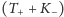 , co dowodzi równości
, co dowodzi równości
Liczby zespolone
O liczbach zespolonych (ich zbiór będziemy oznaczać przez
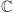 ) możemy
myśleć jak o wektorach (postaci
) możemy
myśleć jak o wektorach (postaci
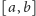 ) na płaszczyźnie. Na liczbach
tych możemy wykonywać działania. Dodawanie wykonuje się dokładnie tak
samo jak dodawanie wektorów. Aby zdefiniować mnożenie, potrzebne są
nam dwa pojęcia. Argumentem liczby zespolonej
) na płaszczyźnie. Na liczbach
tych możemy wykonywać działania. Dodawanie wykonuje się dokładnie tak
samo jak dodawanie wektorów. Aby zdefiniować mnożenie, potrzebne są
nam dwa pojęcia. Argumentem liczby zespolonej
 nazywamy
kąt, który tworzy ona z wektorem
nazywamy
kąt, który tworzy ona z wektorem
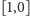 i oznaczamy go przez
i oznaczamy go przez
 (Argument jest dany z dokładnością do
(Argument jest dany z dokładnością do
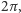 tzn. jeżeli
tzn. jeżeli
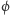 jest argumentem
jest argumentem
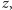 to
to
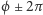 też. W dalszym ciągu ta
niejednoznaczność nie będzie nam przeszkadzała. Przyjmujemy także, że
też. W dalszym ciągu ta
niejednoznaczność nie będzie nam przeszkadzała. Przyjmujemy także, że
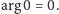 ) Modułem liczby zespolonej
) Modułem liczby zespolonej
 nazywamy długość
wektora reprezentującego
nazywamy długość
wektora reprezentującego
 i oznaczamy go przez
i oznaczamy go przez
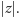 Łatwo
zauważyć, że
Łatwo
zauważyć, że
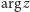 i
i
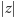 jednoznacznie wyznaczają liczbę
jednoznacznie wyznaczają liczbę
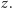
Wynikiem mnożenia dwóch liczb
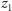 i
i
 jest liczba zespolona
jest liczba zespolona
 o argumencie
o argumencie
 i module
i module

Teraz, gdy umiemy już dodawać i mnożyć, możemy zdefiniować wielomian
zmiennej zespolonej (analogicznie jak wielomian zmiennej rzeczywistej):
wielomianem stopnia
 zmiennej zespolonej
zmiennej zespolonej
 będziemy nazywać
funkcję
będziemy nazywać
funkcję
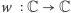 daną wzorem
daną wzorem

gdzie
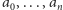 są liczbami zespolonymi oraz
są liczbami zespolonymi oraz
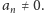
Zasadnicze twierdzenie algebry głosi, że każdy wielomian dodatniego stopnia zmiennej zespolonej ma co najmniej jeden pierwiastek. Jest wiele dowodów tego ważnego twierdzenia, ale lemat Spernera pomoże nam je udowodnić w zaskakująco elementarny sposób.
Kolorowanie
Ustalmy wielomian
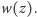 Przez kolorowanie wielomianu nazwiemy
kolorowanie płaszczyzny zespolonej
Przez kolorowanie wielomianu nazwiemy
kolorowanie płaszczyzny zespolonej
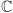 trzema kolorami 0, 1, 2
w zależności od argumentu liczby zespolonej
trzema kolorami 0, 1, 2
w zależności od argumentu liczby zespolonej
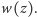 Kolor
Kolor
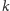 -ty
otrzymają liczby ze zbioru
-ty
otrzymają liczby ze zbioru

Tak pokolorowaną płaszczyznę (Rys. 3) oznaczmy przez
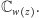
Popatrzmy na kilka przykładów. Jeśli wielomian
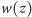 będzie stopnia 0,
to cała płaszczyzna będzie jednokolorowa. Jeśli wielomian będzie postaci
będzie stopnia 0,
to cała płaszczyzna będzie jednokolorowa. Jeśli wielomian będzie postaci
 to płaszczyzna będzie podzielona na trzy przystające
kąty o wspólnym wierzchołku w punkcie
to płaszczyzna będzie podzielona na trzy przystające
kąty o wspólnym wierzchołku w punkcie
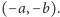 Będzie to wyglądało
tak samo jak na rysunku 3, tylko punkt zbiegu kolorów będzie leżał gdzie
indziej.
Będzie to wyglądało
tak samo jak na rysunku 3, tylko punkt zbiegu kolorów będzie leżał gdzie
indziej.
Aby pokolorować wielomian
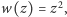 sięgniemy do definicji
mnożenia liczb zespolonych. Mamy
sięgniemy do definicji
mnożenia liczb zespolonych. Mamy
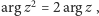 zatem
jeśli punkt
zatem
jeśli punkt
 dostał kolor 0, to
dostał kolor 0, to
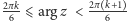 lub
lub
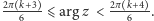 Analogiczne rozumowanie w przypadku
kolorów 1 i 2 prowadzi nas do wniosku, że
Analogiczne rozumowanie w przypadku
kolorów 1 i 2 prowadzi nas do wniosku, że
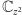 jest podzielona na
sześć przystających kątów o wierzchołkach w punkcie
jest podzielona na
sześć przystających kątów o wierzchołkach w punkcie
 (patrz
rysunek 4).
(patrz
rysunek 4).

Rys. 3 Wielomian
|

Rys. 4 Wielomian
|

Rys. 5 Wielomian
|

Rys. 6 Wielomian
|
Nietrudno się przekonać o tym, że kolorując
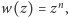 będziemy
musieli namalować
będziemy
musieli namalować
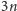 przystających kątów. Będą one miały kolejno
kolory 0, 1, 2, 0, 1, 2 itd.
przystających kątów. Będą one miały kolejno
kolory 0, 1, 2, 0, 1, 2 itd.
Do tej pory szło nam łatwo, ale już w przypadku wielomianu
 napotykamy kłopoty. Z pomocą komputera możemy
wygenerować kolorowanie tego i innych wielomianów (rysunki 5 i 6,
a także okładka). Obserwując obrazki, możemy dojść do dwóch
wniosków:
napotykamy kłopoty. Z pomocą komputera możemy
wygenerować kolorowanie tego i innych wielomianów (rysunki 5 i 6,
a także okładka). Obserwując obrazki, możemy dojść do dwóch
wniosków:
- Łatwo na rysunku znaleźć zera wielomianu. Są to dokładnie te punkty, w których zbiegają się wszystkie trzy kolory.
- Niech
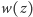 będzie wielomianem stopnia
będzie wielomianem stopnia
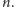 Im dalej
od punktu
Im dalej
od punktu
 tym bardziej kolorowanie
tym bardziej kolorowanie
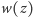 przypomina kolorowanie
przypomina kolorowanie
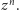
Pierwszy z wniosków wynika z ciągłości
 Dla dowodu drugiego
zauważmy, że przy
Dla dowodu drugiego
zauważmy, że przy
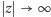 mamy
mamy
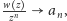 zatem
poza dostatecznie dużym kołem
zatem
poza dostatecznie dużym kołem
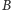 o środku w punkcie
o środku w punkcie
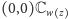 będzie wyglądało prawie jak
będzie wyglądało prawie jak
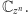
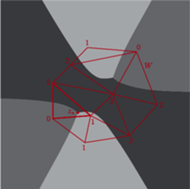
Rys. 7 Ilustracja dowodu zasadniczego twierdzenia algebry. Kolorowanie wielomianu
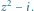 Poza wielokątem
Poza wielokątem
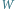 wielomian wygląda jak
wielomian wygląda jak
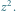
Wiemy zatem, co się dzieje poza dużym kołem
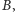 tym bardziej wiemy też,
co się dzieje poza dowolnym wielokątem wypukłym
tym bardziej wiemy też,
co się dzieje poza dowolnym wielokątem wypukłym
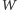 zawierającym to
koło. Nie wiemy jednak, co się dzieje w jego wnętrzu, ale spróbujemy to
odgadnąć, badając jego brzeg. Do tego przyda nam się lemat Spernera.
Dokonajmy triangulacji wielokąta
zawierającym to
koło. Nie wiemy jednak, co się dzieje w jego wnętrzu, ale spróbujemy to
odgadnąć, badając jego brzeg. Do tego przyda nam się lemat Spernera.
Dokonajmy triangulacji wielokąta
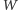 i pokolorujmy jego wierzchołki.
Kolorowanie będzie wyznaczone przez
i pokolorujmy jego wierzchołki.
Kolorowanie będzie wyznaczone przez
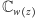 (patrz rysunek 7). Jeśli
trójkąty są dostatecznie małe, to na brzegu pojawią się tylko krawędzie
(patrz rysunek 7). Jeśli
trójkąty są dostatecznie małe, to na brzegu pojawią się tylko krawędzie
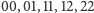 i
i
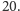 Krawędzi
Krawędzi
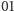 jest dokładnie
jest dokładnie
 (znowu przy założeniu dostatecznie drobnej triangulacji), zatem
(znowu przy założeniu dostatecznie drobnej triangulacji), zatem
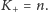
Analogicznie, brak krawędzi
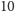 powoduje, że
powoduje, że
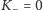 i prawa
strona równania
i prawa
strona równania
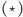 jest równa
jest równa
 Wynika z tego, że
Wynika z tego, że
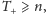 zatem w wielokącie
zatem w wielokącie
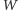 istnieje trójkąt trójkolorowy.
istnieje trójkąt trójkolorowy.
Zdefiniujmy teraz taki ciąg triangulacji
 że średnica
największego trójkąta w
że średnica
największego trójkąta w
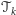 dąży do 0 przy
dąży do 0 przy
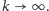 W triangulacji
W triangulacji
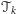 znajdziemy trójkolorowy trójkąt o wierzchołkach
znajdziemy trójkolorowy trójkąt o wierzchołkach
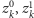 i
i
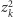 (punkt
(punkt
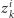 ma kolor
ma kolor
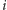 ). Ponieważ ciąg punktów
). Ponieważ ciąg punktów
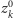 jest
ograniczony przez wielokąt
jest
ograniczony przez wielokąt
 więc na podstawie twierdzenia
Bolzano-Weierstrassa można z niego wybrać podciąg zbieżny
więc na podstawie twierdzenia
Bolzano-Weierstrassa można z niego wybrać podciąg zbieżny
 Z tego, co powiedzieliśmy o średnicach, wynika, że
podciągi
Z tego, co powiedzieliśmy o średnicach, wynika, że
podciągi
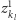 i
i
 również są zbieżne do tej samej granicy
również są zbieżne do tej samej granicy
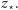
Widać zatem, że w punkcie
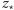 zbiegają się wszystkie trzy kolory,
zatem
zbiegają się wszystkie trzy kolory,
zatem
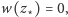 co kończy dowód zasadniczego twierdzenia
algebry.
co kończy dowód zasadniczego twierdzenia
algebry.


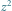
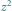
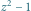
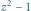
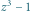
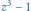
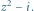 Poza wielokątem
Poza wielokątem
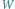 wielomian wygląda jak
wielomian wygląda jak
