Liczby pierwsze i jednoznaczność rozkładu – ogólniej
Twierdzenie o jednoznaczności rozkładu na czynniki pierwsze w zbiorze liczb
naturalnych wypowiada się najprościej w następujący sposób: każdą
liczbę naturalną różną od jedności możemy przedstawić w postaci
iloczynu
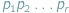 liczb pierwszych na jeden tylko sposób, o ile
rozkłady, różniące się kolejnością czynników, uważać będziemy za
równe...
liczb pierwszych na jeden tylko sposób, o ile
rozkłady, różniące się kolejnością czynników, uważać będziemy za
równe...
Podobne twierdzenie można wysłowić także i dla liczb całkowitych, niekoniecznie dodatnich:
Twierdzenie. Każdą liczbę całkowitą, różną od
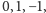 możemy przedstawić na jeden sposób w postaci iloczynu
możemy przedstawić na jeden sposób w postaci iloczynu
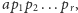 przy czym
przy czym
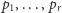 są liczbami pierwszymi,
a liczba
są liczbami pierwszymi,
a liczba
 równa jest
równa jest
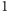 lub
lub
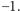
(Oczywiście i w tym przypadku należy utożsamiać rozkłady,
różniące się kolejnością czynników.) Nazwijmy pierścieniem liczbowym
każdy zbiór zawarty w zbiorze liczb zespolonych, w którym wykonalne jest
dodawanie, odejmowanie i mnożenie. Oczywiście, zbiór
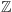 liczb
całkowitych jest takim pierścieniem. Nasuwa się naturalne pytanie, czy
w każdym pierścieniu liczbowym zachodzi twierdzenie analogiczne do
wysłowionego przed chwilą w przypadku pierścienia
liczb
całkowitych jest takim pierścieniem. Nasuwa się naturalne pytanie, czy
w każdym pierścieniu liczbowym zachodzi twierdzenie analogiczne do
wysłowionego przed chwilą w przypadku pierścienia
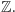
Rozpatrzmy dla przykładu pierścień liczb całkowitych Gaussa, złożony ze
wszystkich liczb zespolonych postaci
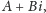 przy czym
przy czym
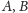 są
liczbami całkowitymi. O tym pierścieniu można udowodnić następujące
twierdzenie, analogiczne do twierdzenia o jednoznacznym rozkładzie w
są
liczbami całkowitymi. O tym pierścieniu można udowodnić następujące
twierdzenie, analogiczne do twierdzenia o jednoznacznym rozkładzie w
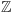 :
:
Twierdzenie. Jeśli
 jest liczbą całkowitą Gaussa, różną od
jest liczbą całkowitą Gaussa, różną od
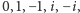 to możemy ją przedstawić w postaci
to możemy ją przedstawić w postaci

przy czym liczby
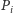 są liczbami pierwszymi Gaussa, tj. mają tę
własność, że z rozkładu
są liczbami pierwszymi Gaussa, tj. mają tę
własność, że z rozkładu
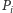 na czynniki,
na czynniki,
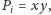 gdzie
gdzie
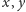 są liczbami całkowitymi Gaussa, wynika, że jeden z tych
czynników jest równy,
są liczbami całkowitymi Gaussa, wynika, że jeden z tych
czynników jest równy,
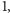
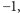
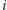 lub
lub
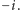
Jeżeli

jest innym rozkładem tego typu, to
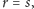 a przy tym po odpowiednim
przenumerowaniu liczb
a przy tym po odpowiednim
przenumerowaniu liczb
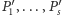 zachodzą równości:
zachodzą równości:
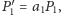
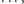
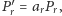 przy czym każda z liczb
przy czym każda z liczb
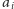 jest równa
jest równa
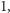
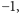
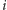 lub
lub
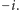
Dla przykładu rozłożymy na czynniki pierwsze w pierścieniu Gaussa liczbę 2:
mamy równość:
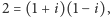 a rozkład ten jest rozkładem na
czynniki pierwsze, bo jeśli np.
a rozkład ten jest rozkładem na
czynniki pierwsze, bo jeśli np.
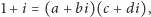 to
to

a zatem
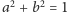 lub też
lub też
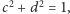 co pokazuje, że jedna
z liczb
co pokazuje, że jedna
z liczb
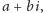
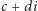 jest równa
jest równa
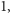
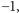
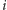 lub
lub
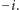
Możemy przy tym także napisać:

co pokazuje, że możliwości podane w sformułowaniu twierdzenia rzeczywiście występują.
By móc sensownie sformułować twierdzenie o jednoznaczności rozkładu dla
dowolnego pierścienia liczbowego, należy uprzednio określić, co będziemy
rozumieli przez liczby pierwsze w takim pierścieniu i jakie liczby będą
grały role liczb
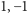 w pierścieniu liczb całkowitych, czy też
liczb
w pierścieniu liczb całkowitych, czy też
liczb
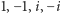 w pierścieniu Gaussa. W tym celu zauważmy,
że odwrotność każdej z liczb
w pierścieniu Gaussa. W tym celu zauważmy,
że odwrotność każdej z liczb
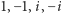 również leży
w pierścieniu Gaussa.
również leży
w pierścieniu Gaussa.
To podsuwa następujące określenie: jeżeli
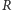 jest pierścieniem liczbowym,
to liczba
jest pierścieniem liczbowym,
to liczba
 należąca do niego nazywa się odwracalna w
należąca do niego nazywa się odwracalna w
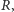 jeżeli
jeżeli
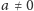 oraz
oraz
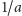 należy do
należy do
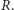 (Oczywiście, liczby
(Oczywiście, liczby
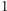 i
i
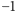 są odwracalne w każdym pierścieniu, a przykład pierścienia
Gaussa pokazuje, że liczb odwracalnych może być więcej.) Teraz możemy
określić liczby pierwsze w pierścieniu
są odwracalne w każdym pierścieniu, a przykład pierścienia
Gaussa pokazuje, że liczb odwracalnych może być więcej.) Teraz możemy
określić liczby pierwsze w pierścieniu
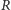 : różną od zera liczbę
: różną od zera liczbę
 pierścienia
pierścienia
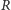 nazywamy liczbą pierwszą w
nazywamy liczbą pierwszą w
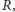 jeżeli
z równości
jeżeli
z równości
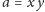 (
(
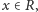
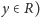 wynika, że jedna
z liczb
wynika, że jedna
z liczb
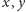 jest odwracalna w
jest odwracalna w
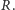
Używając tych definicji, możemy teraz sformułować dla dowolnego
pierścienia liczbowego
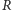 odpowiednik twierdzenia o jednoznaczności
rozkładu:
odpowiednik twierdzenia o jednoznaczności
rozkładu:
Twierdzenie.
W pierścieniu
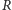 zachodzi twierdzenie o jednoznaczności rozkładu,
jeżeli każda liczba
zachodzi twierdzenie o jednoznaczności rozkładu,
jeżeli każda liczba
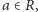 różna od zera i nieodwracalna da się
zapisać w postaci
różna od zera i nieodwracalna da się
zapisać w postaci

przy czym liczby
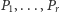 są liczbami
pierwszymi w
są liczbami
pierwszymi w
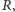 a przy tym jeżeli
a przy tym jeżeli
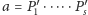 jest innym
takim rozkładem, to
jest innym
takim rozkładem, to
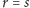 i po odpowiednim ponumerowaniu liczb
i po odpowiednim ponumerowaniu liczb
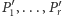 zachodzą równości:
zachodzą równości:

przy czym liczby
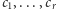 są odwracalne.
są odwracalne.
Następujący przykład świadczy o tym, że sformułowane powyżej twierdzenie nie we wszystkich pierścieniach liczbowych jest prawdziwe:
Przykład. Rozpatrzmy pierścień
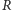 złożony ze wszystkich liczb
złożony ze wszystkich liczb
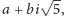 przy
przy
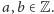 (Proponuję Czytelnikowi
sprawdzenie, że
(Proponuję Czytelnikowi
sprawdzenie, że
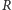 w istocie jest pierścieniem.) Liczba 6 ma w
w istocie jest pierścieniem.) Liczba 6 ma w
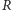 dwa różne rozkłady:
dwa różne rozkłady:

Nietrudno sprawdzić, że występujące tu czynniki są liczbami pierwszymi
w rozważanym pierścieniu. Jeżeli np.
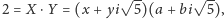 przy czym
przy czym
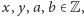 to
to

a więc
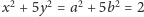 lub też jedna z liczb
lub też jedna z liczb
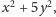
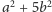 jest równa 1, a druga równa 4. Ponieważ równanie
jest równa 1, a druga równa 4. Ponieważ równanie
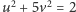 nie ma rozwiązań całkowitych, musi zachodzić druga
możliwość, a wówczas jedna z liczb
nie ma rozwiązań całkowitych, musi zachodzić druga
możliwość, a wówczas jedna z liczb
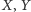 musi być równa
1 lub
musi być równa
1 lub
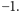 Podobnie sprawdzamy, że pozostałe
czynniki naszych rozkładów są pierwsze. Pozostaje sprawdzić, że ilorazy
czynników obu rozkładów nie są odwracalne, ale to wynika z uwagi, że
żadna z liczb
Podobnie sprawdzamy, że pozostałe
czynniki naszych rozkładów są pierwsze. Pozostaje sprawdzić, że ilorazy
czynników obu rozkładów nie są odwracalne, ale to wynika z uwagi, że
żadna z liczb
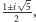
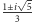 nie leży w
nie leży w
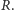 Widzimy
ostatecznie, że w pierścieniu
Widzimy
ostatecznie, że w pierścieniu
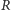 twierdzenie o jednoznaczności
rozkładu nie zachodzi.
twierdzenie o jednoznaczności
rozkładu nie zachodzi.