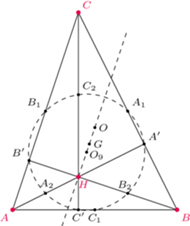
Układ ortocentryczny

Przed rozpoczęciem lektury niniejszego kącika warto zapoznać się z poprzednim, w którym zdefiniowany został układ ortocentryczny (na rysunku 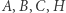) oraz jego spodki 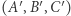, odcinki 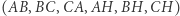i środki tych odcinków .

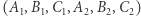Poruszając temat układów ortocentrycznych, byłoby nietaktem pominąć dwa słynne twierdzenia z nimi związane: o okręgu dziewięciu punktów i o prostej Eulera.

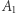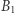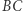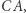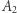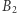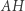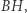Punkty i są środkami boków i a punkty i - odcinków i więc 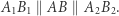Analogicznie dowodzimy, że 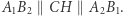Proste 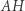i 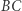są prostopadłe, więc czworokąt 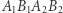jest prostokątem. Z tego wynika, że odcink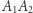i i 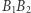są równej długości i mają wspólny środek. 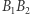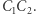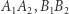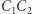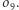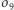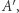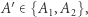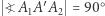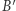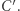To samo można udowodnić dla odcinków i Te trzy odcinki - i - są zatem średnicami tego samego okręgu - nazwijmy go Na okręgu leży również punkt gdyż albo albo ; analogicznie jest dla punktów i Okrąg 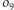to słynny okrąg dziewięciu punktów trójkąta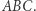

Trójkąt 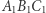jest jednokładny do trójkąta 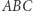w stosunku 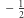względem ich wspólnego środka ciężkości 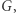zatem opisane na nich okręgi i 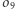również są jednokładne względem 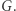Z tego wynika, że punkt 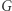leży na odcinku 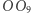łączącym środki tych okręgów, przy czym 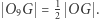Co więcej, trójkąt 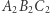jest jednokładny do trójkąta 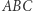w stosunku 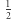względem punktu 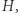więc punkt 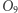jest środkiem odcinka 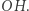Z tego wynika, że punkty 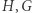i 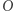leżą w tej kolejności na jednej prostej i zachodzi równość 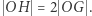Nazywamy ją prostą Eulera trójkąta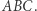

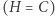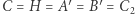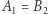Na koniec zauważmy, że w przypadku zdegenerowanego układu ortocentrycznego zachodzą równości oraz i 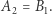Poza tym, że prostokąt 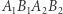degeneruje się do odcinka, nie dzieje się nic, co mogłoby zaszkodzić przeprowadzonemu wyżej rozumowaniu.