Kącik początkującego olimpijczyka
Rachunki
Kochajcie trygonometrię, dziewczęta
O stosowaniu trygonometrii w zadaniach olimpijskich.
Trygonometria, z zupełnie niezrozumiałych dla mnie powodów, bywa uznawana za brzydką metodę rozwiązywania zadań olimpijskich. Niestety skutkuje to tym, że młodzież mniej chętnie uczy się tego ważnego działu matematyki. Być może znalezienie odcinka, którego dorysowanie natychmiast rozwiązuje problem, jest nieco bardziej eleganckie niż stosowanie twierdzenia sinusów, ale nie ma gwarancji, że taki odcinek zdążymy w czasie zawodów znaleźć. Dlatego warto w swym arsenale mieć dodatkowe narzędzia, które, choć bardziej toporne, w niektórych warunkach są nieco pewniejsze.
W poniższych twierdzeniach używamy standardowych oznaczeń: niech 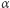 ,
, 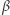 ,
, 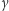 będą miarami kątów przy wierzchołkach odpowiednio
będą miarami kątów przy wierzchołkach odpowiednio 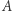 ,
, 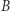 ,
, 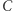 trójkąta
trójkąta 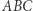 , zaś
, zaś 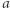 ,
, 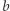 ,
,  - długościami boków naprzeciw nich. Przez
- długościami boków naprzeciw nich. Przez 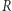 oznaczamy promień okręgu opisanego na tym trójkącie.
oznaczamy promień okręgu opisanego na tym trójkącie.
Nie będziemy wymieniać tu wzorów redukcyjnych ani innych tożsamości trygonometrycznych. Czytelnik, jeżeli jeszcze nie zapoznał się z nimi na lekcji matematyki w szkole średniej, znajdzie je w tablicach matematycznych.
Na koniec dwie uwagi do twierdzenia sinusów. Wynika z niego równość proporcji 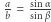 (i dwie analogiczne), więc możemy płynnie przechodzić pomiędzy długościami boków i sinusami kątów trójkąta. Ponadto do korzystania z twierdzenia sinusów wcale nam trójkąta nie potrzeba, gdyż łączy ono długość
(i dwie analogiczne), więc możemy płynnie przechodzić pomiędzy długościami boków i sinusami kątów trójkąta. Ponadto do korzystania z twierdzenia sinusów wcale nam trójkąta nie potrzeba, gdyż łączy ono długość 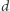 cięciwy okręgu, która wyznacza kąt wpisany
cięciwy okręgu, która wyznacza kąt wpisany 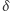 , z promieniem
, z promieniem 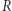 tego okręgu:
tego okręgu: 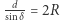 .
.
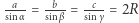
![|[ABC]](/math/temat/matematyka/geometria/2020/01/29/kochajcie-trygonometrie-dziewczeta/5x-1014fd95293424119b8d56dd3b7ba6cea31b9cb5-im-33,33,33-FF,FF,FF.gif)