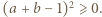Funkcja 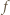 jest ciągła i rosnąca, a jej granice przy końcach dziedziny
jest ciągła i rosnąca, a jej granice przy końcach dziedziny 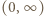 wynoszą 0 oraz
wynoszą 0 oraz 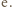 Zatem liczba
Zatem liczba 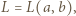 dla której
dla której 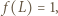 jest jednoznacznie określona. Wykażemy, że
jest jednoznacznie określona. Wykażemy, że 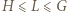 (gdzie
(gdzie 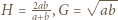 ); stąd też wyniknie, że
); stąd też wyniknie, że 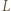 leży pomiędzy
leży pomiędzy 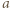 i
i 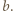 Wobec ścisłej monotoniczności funkcji
Wobec ścisłej monotoniczności funkcji 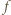 wystarczy dowieść, że
wystarczy dowieść, że 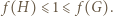
Niech 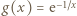 dla
dla 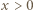 ; jest to funkcja rosnąca. Skoro
; jest to funkcja rosnąca. Skoro 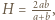 zatem
zatem
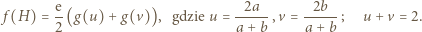 |
(1) |
Badając znak 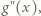 stwierdzamy, że funkcja
stwierdzamy, że funkcja 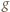 jest wklęsła w przedziale
jest wklęsła w przedziale 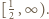 Jeżeli więc liczby
Jeżeli więc liczby 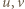 leżą w tym przedziale, to
leżą w tym przedziale, to 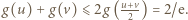 Jeśli zaś np.
Jeśli zaś np. 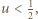 rozważamy dwa podprzypadki (pamiętając, że
rozważamy dwa podprzypadki (pamiętając, że 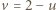 ):
):
we wszystkich przypadkach uzyskane wartości nie przekraczają 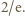 Otrzymane oszacowanie
Otrzymane oszacowanie 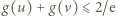 pokazuje (zgodnie ze wzorem (1)), że
pokazuje (zgodnie ze wzorem (1)), że 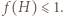
Pozostało do wykazania, że 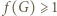 ; do tego użyjemy funkcji
; do tego użyjemy funkcji 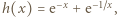 bowiem
bowiem
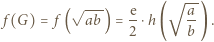 |
(2) |
Nietrudno się przekonać, że dla 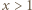 zachodzi nierówność
zachodzi nierówność 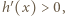 czyli
czyli 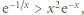 równoważna (przez logarytmowanie) nierówności
równoważna (przez logarytmowanie) nierówności 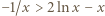 ; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie
; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie 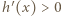 dla
dla 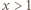 ; stąd
; stąd 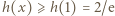 dla
dla 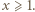 Ponieważ bez straty ogólności można przyjąć, że
Ponieważ bez straty ogólności można przyjąć, że 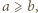 ze wzoru (2) wnosimy, że
ze wzoru (2) wnosimy, że 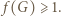 To kończy rozwiązanie.
To kończy rozwiązanie.
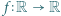 ma tę własność, że każda z funkcji
ma tę własność, że każda z funkcji 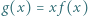 oraz
oraz 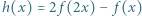 ma granicę 0 przy
ma granicę 0 przy 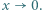 Czy wynika stąd, że także funkcja
Czy wynika stąd, że także funkcja 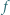 ma granicę 0 przy
ma granicę 0 przy 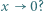
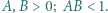
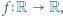
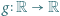
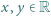

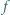
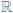
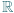 ; ma więc funkcję odwrotną
; ma więc funkcję odwrotną 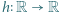
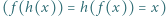 . Udowodnić, że funkcja
. Udowodnić, że funkcja 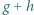
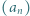 jest określony wzorami
jest określony wzorami 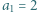 ;
; 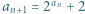 dla
dla 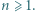 Niech
Niech 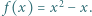 Udowodnić, że dla każdego
Udowodnić, że dla każdego 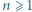 liczba
liczba 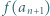 dzieli się przez
dzieli się przez 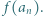
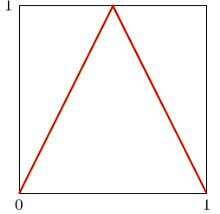
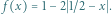
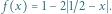
![| f [0,1] [0,1]](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/1x-6ef1c75cd7890fac5a5a10e6c2a3afccfa359dba-im-2C,6B,73-FF,FF,FF.gif) będzie dane wzorem
będzie dane wzorem 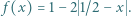 Niech ponadto
Niech ponadto 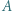 oraz
oraz 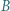 będą dowolnymi niepustymi przedziałami (otwartymi lub domkniętymi jedno- lub obustronnie), których końce są liczbami niewymiernymi. Uzasadnić, że istnieje takie
będą dowolnymi niepustymi przedziałami (otwartymi lub domkniętymi jedno- lub obustronnie), których końce są liczbami niewymiernymi. Uzasadnić, że istnieje takie 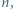 że
że 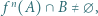 gdzie
gdzie 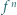 oznacza
oznacza  -krotne złożenie funkcji
-krotne złożenie funkcji 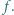
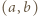 ma tę własność, że
ma tę własność, że ![fn((a,b)) = [0,1]](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/2x-3582530a21981c4662de24aae4547af0402ec105-im-66,57,43-FF,FF,FF.gif) dla pewnego
dla pewnego 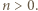 Niech
Niech 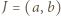 i
i 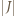 będzie długością tego przedziału. Zauważmy, że jeżeli
będzie długością tego przedziału. Zauważmy, że jeżeli 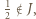 to
to 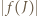 jest przedziałem dwukrotnie dłuższym niż
jest przedziałem dwukrotnie dłuższym niż 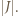 Tym samym kolejne przekształcenia
Tym samym kolejne przekształcenia 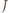 przez
przez 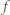 są przedziałami długości
są przedziałami długości 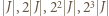 i tak dalej, o ile do żadnego z wymienionych zbiorów nie należy
i tak dalej, o ile do żadnego z wymienionych zbiorów nie należy 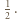 Wobec powyższego istnieje takie
Wobec powyższego istnieje takie 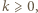 że
że 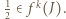 Ale
Ale 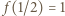 i
i 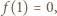 czyli
czyli 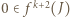 i wobec tego
i wobec tego 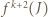 jest przedziałem postaci
jest przedziałem postaci 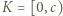 dla pewnego
dla pewnego 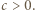 Teraz
Teraz 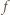 ponownie podwaja długość przedziału
ponownie podwaja długość przedziału 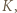 wobec tego dla pewnego
wobec tego dla pewnego 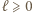 zachodzi
zachodzi 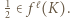 Tym samym
Tym samym ![[0, | 1/2]⊂ fℓ(K)](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/25x-3582530a21981c4662de24aae4547af0402ec105-im-66,57,43-FF,FF,FF.gif) i wystarczy jeszcze zauważyć, że
i wystarczy jeszcze zauważyć, że![[0,1] = f ([0,1/2]) ⊂ fℓ+1(K) = fℓ+1( fk+2(J)) = fk+ℓ+3(J).](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/26x-3582530a21981c4662de24aae4547af0402ec105-dm-66,57,43-FF,FF,FF.gif)
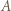 postulowany w treści zadania zawiera w sobie przedział otwarty oraz jeśli
postulowany w treści zadania zawiera w sobie przedział otwarty oraz jeśli 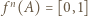 z przypadku ogólnego, to tym bardziej
z przypadku ogólnego, to tym bardziej 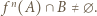
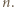
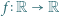 spełniające dla wszystkich
spełniające dla wszystkich 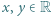 nierówność
nierówność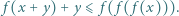
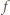 spełnia warunki zadania. Niech
spełnia warunki zadania. Niech 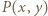 oznacza nierówność
oznacza nierówność 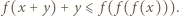 Wybierzmy dowolnie
Wybierzmy dowolnie 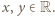 Ponieważ
Ponieważ 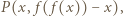 więc
więc 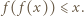 Podstawiając w ostatniej nierówności
Podstawiając w ostatniej nierówności 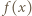 zamiast
zamiast  i uwzględniając
i uwzględniając 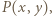 dostajemy
dostajemy 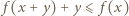 dla dowolnych
dla dowolnych 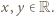 Podstawiając
Podstawiając 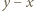 zamiast
zamiast 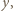 dostajemy
dostajemy 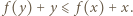 Z dowolności
Z dowolności 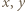 wnioskujemy, że
wnioskujemy, że 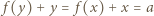 dla pewnego
dla pewnego 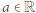 i wszystkich
i wszystkich 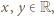 zatem musi być
zatem musi być 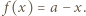 Łatwo sprawdzić, że ta funkcja faktycznie spełnia
Łatwo sprawdzić, że ta funkcja faktycznie spełnia 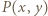 dla wszystkich
dla wszystkich 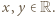
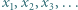 będzie rosnącym ciągiem wszystkich dodatnich liczb
będzie rosnącym ciągiem wszystkich dodatnich liczb 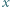 spełniających równanie
spełniających równanie 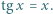 Niech
Niech 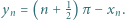 Obliczyć granicę ciągu
Obliczyć granicę ciągu 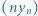 przy
przy 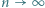 (lub wykazać, że granica nie istnieje).
(lub wykazać, że granica nie istnieje).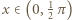 zachodzi nierówność
zachodzi nierówność 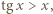 więc w tym przedziale nie leży żaden wyraz ciągu
więc w tym przedziale nie leży żaden wyraz ciągu 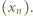 W każdym dalszym przedziale dodatniości funkcji tangens leży jeden wyraz. Tak więc
W każdym dalszym przedziale dodatniości funkcji tangens leży jeden wyraz. Tak więc 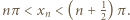 Wobec określenia
Wobec określenia 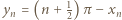 wynika stąd, że
wynika stąd, że 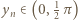 oraz
oraz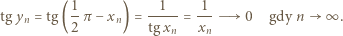
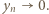 A skoro
A skoro 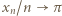 (oraz
(oraz 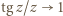 gdy
gdy 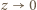 ), zatem
), zatem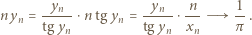
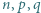 będą liczbami całkowitymi dodatnimi. Ciąg liczb całkowitych
będą liczbami całkowitymi dodatnimi. Ciąg liczb całkowitych 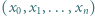 spełnia warunki:
spełnia warunki: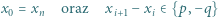
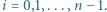 Udowodnić, że jeżeli
Udowodnić, że jeżeli 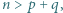 to istnieją takie
to istnieją takie 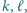 że
że 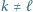 i
i 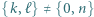 oraz
oraz 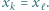
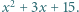 Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy
Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy  albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian
albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian 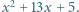 Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.
Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.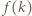 będzie wartością danego trójmianu w punkcie
będzie wartością danego trójmianu w punkcie 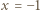 po zmianie współczynników przez
po zmianie współczynników przez 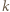 -tego ucznia i niech
-tego ucznia i niech 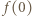 będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że
będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że 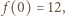 a
a 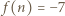 (gdzie
(gdzie 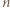 to numer ostatniego ucznia). Ponadto zachodzi nierówność
to numer ostatniego ucznia). Ponadto zachodzi nierówność 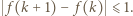 Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o
Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o 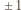 wartość współczynnika przy
wartość współczynnika przy 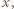 dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie
dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie 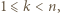 że
że 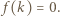 Zatem w pewnym momencie na tablicy był napisany trójmian
Zatem w pewnym momencie na tablicy był napisany trójmian 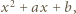 którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita
którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita 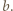
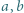 określamy funkcję
określamy funkcję 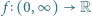 wzorem
wzorem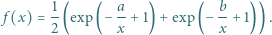
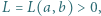 dla której
dla której 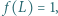 i że
i że 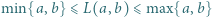 ; zatem liczba
; zatem liczba 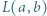 może być uważana za pewną średnią liczb
może być uważana za pewną średnią liczb 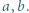
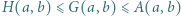 między średnimi: harmoniczną, geometryczną i arytmetyczną liczb
między średnimi: harmoniczną, geometryczną i arytmetyczną liczb 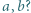
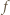 jest ciągła i rosnąca, a jej granice przy końcach dziedziny
jest ciągła i rosnąca, a jej granice przy końcach dziedziny 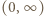 wynoszą 0 oraz
wynoszą 0 oraz 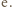 Zatem liczba
Zatem liczba 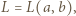 dla której
dla której 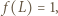 jest jednoznacznie określona. Wykażemy, że
jest jednoznacznie określona. Wykażemy, że 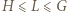 (gdzie
(gdzie 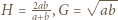 ); stąd też wyniknie, że
); stąd też wyniknie, że 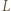 leży pomiędzy
leży pomiędzy 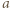 i
i 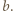 Wobec ścisłej monotoniczności funkcji
Wobec ścisłej monotoniczności funkcji 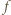 wystarczy dowieść, że
wystarczy dowieść, że 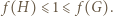
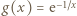 dla
dla 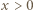 ; jest to funkcja rosnąca. Skoro
; jest to funkcja rosnąca. Skoro 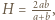 zatem
zatem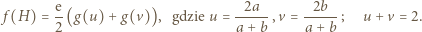
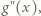 stwierdzamy, że funkcja
stwierdzamy, że funkcja 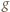 jest wklęsła w przedziale
jest wklęsła w przedziale 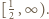 Jeżeli więc liczby
Jeżeli więc liczby 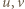 leżą w tym przedziale, to
leżą w tym przedziale, to 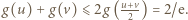 Jeśli zaś np.
Jeśli zaś np. 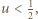 rozważamy dwa podprzypadki (pamiętając, że
rozważamy dwa podprzypadki (pamiętając, że 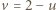 ):
):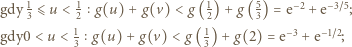
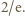 Otrzymane oszacowanie
Otrzymane oszacowanie 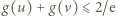 pokazuje (zgodnie ze wzorem (1)), że
pokazuje (zgodnie ze wzorem (1)), że 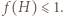
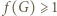 ; do tego użyjemy funkcji
; do tego użyjemy funkcji 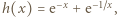 bowiem
bowiem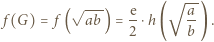
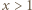 zachodzi nierówność
zachodzi nierówność 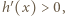 czyli
czyli 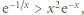 równoważna (przez logarytmowanie) nierówności
równoważna (przez logarytmowanie) nierówności 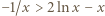 ; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie
; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie 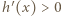 dla
dla 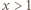 ; stąd
; stąd 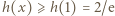 dla
dla 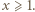 Ponieważ bez straty ogólności można przyjąć, że
Ponieważ bez straty ogólności można przyjąć, że 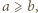 ze wzoru (2) wnosimy, że
ze wzoru (2) wnosimy, że 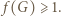 To kończy rozwiązanie.
To kończy rozwiązanie.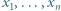 należą do odcinka
należą do odcinka ![[0,1].](/math/temat/matematyka/analiza/zadania/2020/02/29/zm-1632/2x-a703a273548e97ab80323cc80e76f4c2e0b71aa8-im-2C,6B,73-FF,FF,FF.gif) Udowodnić, że istnieje takie
Udowodnić, że istnieje takie 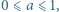 że
że 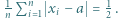
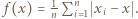 Ponieważ
Ponieważ 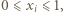 więc
więc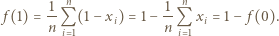
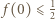 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 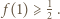 Teza wynika zatem z ciągłości funkcji
Teza wynika zatem z ciągłości funkcji 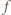 i własności Darboux funkcji ciągłych.
i własności Darboux funkcji ciągłych.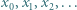 jest określony rekurencyjnie:
jest określony rekurencyjnie: 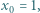
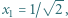
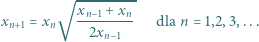
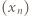 wynika (przez oczywistą indukcję), że wszystkie jego wyrazy są dobrze określonymi liczbami dodatnimi. Weźmy pod uwagę ilorazy
wynika (przez oczywistą indukcję), że wszystkie jego wyrazy są dobrze określonymi liczbami dodatnimi. Weźmy pod uwagę ilorazy 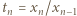 ; ciąg liczb dodatnich
; ciąg liczb dodatnich 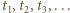 z wyrazem początkowym
z wyrazem początkowym 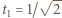 spełnia zależność rekurencyjną
spełnia zależność rekurencyjną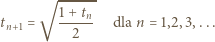
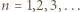 zachodzi równość
zachodzi równość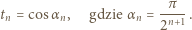
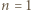 tak jest. Przyjmijmy równość
tak jest. Przyjmijmy równość 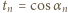 dla pewnego
dla pewnego 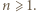 Ponieważ
Ponieważ 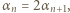 mamy wówczas
mamy wówczas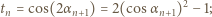
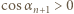 ):
):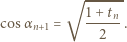
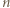 zastąpionym przez
zastąpionym przez 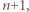 czyli tezę indukcyjną.
czyli tezę indukcyjną.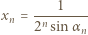
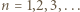 Znów indukcja: dla
Znów indukcja: dla 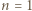 zgadza się (bo
zgadza się (bo 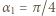 ). Ustalmy
). Ustalmy 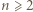 i przyjmijmy słuszność (3) z
i przyjmijmy słuszność (3) z 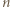 zastąpionym przez
zastąpionym przez 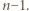 Z takiego założenia indukcyjnego i ze wzoru (2) otrzymujemy
Z takiego założenia indukcyjnego i ze wzoru (2) otrzymujemy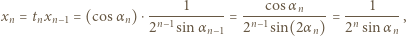
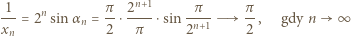
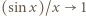 przy
przy 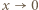 ). Stąd, ostatecznie,
). Stąd, ostatecznie, 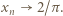
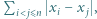 gdzie
gdzie ![x ∈[0,1] i](/math/temat/matematyka/analiza/zadania/2019/12/31/zm-1624/2x-7a859bc2426be6efd74caf08c9abc8e565add91b-im-2C,6B,73-FF,FF,FF.gif) dla
dla 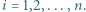
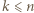 oraz dowolne wartości zmiennych
oraz dowolne wartości zmiennych ![x ∈[0,1] i](/math/temat/matematyka/analiza/zadania/2019/12/31/zm-1624/2x-e2b79e992298491a1812318ec88526ecbe876e9b-im-66,57,43-FF,FF,FF.gif) dla
dla 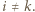 Wówczas wyrażenie
Wówczas wyrażenie 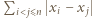 możemy traktować jako funkcję zmiennej
możemy traktować jako funkcję zmiennej 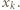 Jest to funkcja ściśle wypukła, jako suma ściśle wypukłych funkcji
Jest to funkcja ściśle wypukła, jako suma ściśle wypukłych funkcji 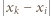 dla
dla 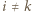 oraz stałych
oraz stałych 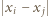 dla
dla 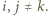 W tej sytuacji największa wartość tej funkcji jest przyjmowana na krańcach dziedziny, tj. dla
W tej sytuacji największa wartość tej funkcji jest przyjmowana na krańcach dziedziny, tj. dla 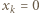 lub
lub 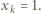 Z dowolności wyboru
Z dowolności wyboru 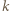 wnioskujemy, że największa wartość badanego wyrażenia jest przyjmowana dla pewnej konfiguracji
wnioskujemy, że największa wartość badanego wyrażenia jest przyjmowana dla pewnej konfiguracji 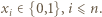 Jeśli
Jeśli 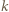 spośród zmiennych
spośród zmiennych 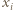 jest równe 1, to rozważana suma ma wartość
jest równe 1, to rozważana suma ma wartość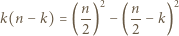
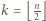 równą
równą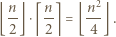
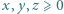 przyjmijmy:
przyjmijmy: 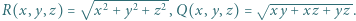 Wyznaczyć najmniejszą możliwą wartość wyrażenia
Wyznaczyć najmniejszą możliwą wartość wyrażenia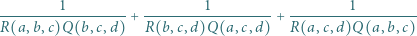
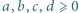 spełniających warunek
spełniających warunek 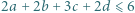 oraz wyznaczyć wszystkie czwórki
oraz wyznaczyć wszystkie czwórki 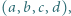 dla których to minimum jest osiągane.
dla których to minimum jest osiągane.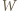 (stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):
(stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):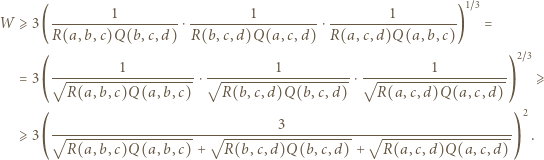
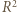 i
i 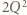 ), dostajemy oszacowanie
), dostajemy oszacowanie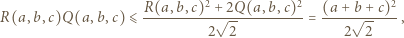
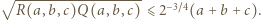 Stąd i z analogicznego oszacowania dla trójek
Stąd i z analogicznego oszacowania dla trójek 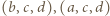 uzyskujemy kontynuację wcześniejszego ciągu nierówności:
uzyskujemy kontynuację wcześniejszego ciągu nierówności: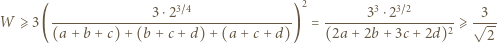
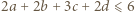 z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy
z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy 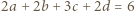 oraz
oraz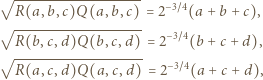
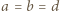 oraz
oraz 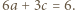 Ponadto - oznaczając krótko
Ponadto - oznaczając krótko 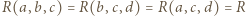 (i podobnie
(i podobnie 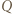 ) - musimy mieć równość
) - musimy mieć równość 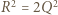 (do takiej pary też była stosowana nierówność między średnimi) - czyli
(do takiej pary też była stosowana nierówność między średnimi) - czyli 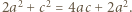 Wraz z równością
Wraz z równością 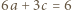 daje to alternatywę:
daje to alternatywę: 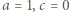 lub
lub 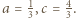 Dla czwórek
Dla czwórek 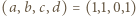 oraz
oraz 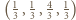 wyznaczone oszacowanie
wyznaczone oszacowanie 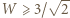 przechodzi w równość. Zatem szukane minimum wynosi
przechodzi w równość. Zatem szukane minimum wynosi 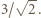
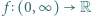 jest dana wzorem
jest dana wzorem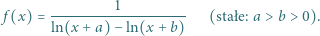
 ), i znaleźć równanie tej asymptoty.
), i znaleźć równanie tej asymptoty.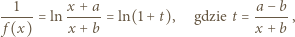
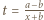 dąży do 0, gdy
dąży do 0, gdy 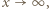 zatem
zatem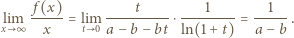
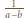 ; wystarczy zatem, by następująca różnica miała skończoną granicę (przy
; wystarczy zatem, by następująca różnica miała skończoną granicę (przy 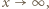 czyli
czyli 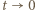 ):
):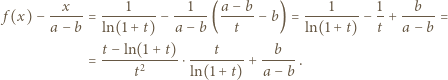
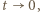 pierwszy z ilorazów (w ostatnim uzyskanym wyrażeniu) dąży do granicy 1/2 (bo
pierwszy z ilorazów (w ostatnim uzyskanym wyrażeniu) dąży do granicy 1/2 (bo 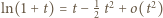 ). Stąd wniosek, że asymptotą (przy
). Stąd wniosek, że asymptotą (przy  ) jest prosta o równaniu
) jest prosta o równaniu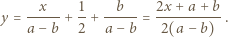
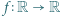 spełniające równanie
spełniające równanie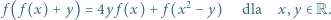
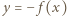 oraz
oraz 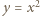 ; otrzymujemy równania
; otrzymujemy równania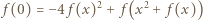
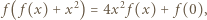
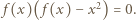 Zatem dla każdej liczby
Zatem dla każdej liczby 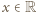 ma miejsce alternatywa:
ma miejsce alternatywa: 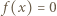 lub
lub 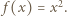 Stąd, w szczególności,
Stąd, w szczególności, 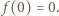
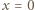 jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 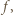 to
to 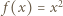 dla wszystkich
dla wszystkich  Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy
Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy 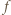 ma jeszcze jakieś miejsce zerowe
ma jeszcze jakieś miejsce zerowe 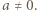 Wykażemy, że wówczas
Wykażemy, że wówczas 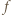 jest tożsamościowo równa zeru.
jest tożsamościowo równa zeru.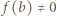 dla pewnego
dla pewnego 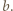 Biorąc w zadanym równaniu
Biorąc w zadanym równaniu 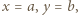 dostajemy
dostajemy 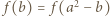 ; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie
; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie 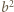 oraz
oraz 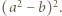 Przyrównanie tych wartości daje równość
Przyrównanie tych wartości daje równość 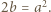 To liczba dodatnia; stąd
To liczba dodatnia; stąd 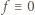 w przedziale
w przedziale ![|(−∞ ,0].](/math/temat/matematyka/analiza/zadania/2019/10/31/zm-k44-789/9x-86016eea9da0a9d7e7b58d20a6007ab7e898b219-im-66,57,43-FF,FF,FF.gif) Weźmy teraz dowolną liczbę
Weźmy teraz dowolną liczbę 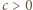 i w wyjściowym równaniu podstawmy
i w wyjściowym równaniu podstawmy 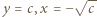 (już wiemy, że
(już wiemy, że 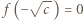 ). Wychodzi
). Wychodzi 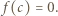 Tak więc
Tak więc 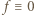 także w przedziale
także w przedziale 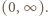
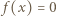 (dla wszystkich
(dla wszystkich 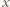 ) oraz
) oraz  (dla wszystkich
(dla wszystkich  ).
).

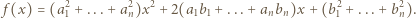
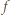 przyjmuje wyłącznie wartości nieujemne, więc
przyjmuje wyłącznie wartości nieujemne, więc 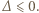 Jest to nierówność równoważna dowodzonej.
Jest to nierówność równoważna dowodzonej.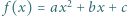 spełnia dla każdego
spełnia dla każdego ![|x∈ [−1,1]](/math/temat/matematyka/analiza/zadania/2019/09/30/zm-19_10-kpo-8/2x-74a6438c69d0f6ea8ca78cf3a770b01ff3c09138-im-2C,6B,73-FF,FF,FF.gif) nierówność
nierówność 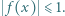 Wyznaczyć największą możliwą wartość wyrażenia
Wyznaczyć największą możliwą wartość wyrażenia 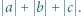
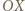 i
i 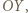 można założyć bez utraty ogólności, że
można założyć bez utraty ogólności, że 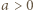 i
i 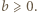 Jeśli
Jeśli 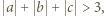 to
to 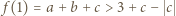 oraz
oraz 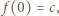 więc
więc 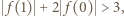 czyli
czyli 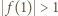 lub
lub 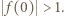 Wartość
Wartość 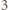 jest osiągalna, na przykład dla funkcji
jest osiągalna, na przykład dla funkcji 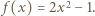
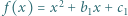 i
i 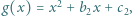 których współczynniki są rzeczywiste i spełniają warunek
których współczynniki są rzeczywiste i spełniają warunek
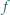 i
i 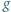 mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.
mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.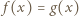 ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie 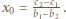 Wówczas
Wówczas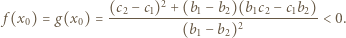
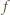 i
i 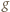 przecinają się tylko w jednym punkcie, leżącym poniżej osi
przecinają się tylko w jednym punkcie, leżącym poniżej osi 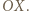 Resztę załatwia własność Darboux.
Resztę załatwia własność Darboux.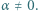 Funkcja
Funkcja 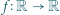 spełnia dla każdej pary liczb rzeczywistych
spełnia dla każdej pary liczb rzeczywistych 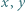 równanie
równanie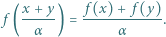
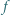 spełnia dla każdej pary liczb rzeczywistych
spełnia dla każdej pary liczb rzeczywistych 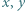 równanie
równanie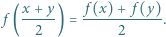
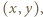 a drugi raz dla
a drugi raz dla 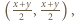 uzyskujemy
uzyskujemy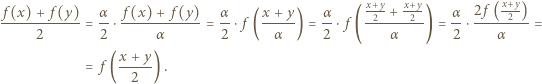
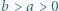 oraz parzystej liczby naturalnej
oraz parzystej liczby naturalnej 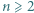 wyznaczyć kres górny wartości stosunku
wyznaczyć kres górny wartości stosunku 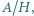 gdzie
gdzie 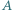 i
i 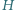 to (odpowiednio) średnia arytmetyczna i średnia harmoniczna
to (odpowiednio) średnia arytmetyczna i średnia harmoniczna 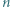 liczb wybranych dowolnie z przedziału
liczb wybranych dowolnie z przedziału ![[a,b].](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/7x-ef372a8dfa93edadbc34939244d39cca0f9e4c26-im-2C,6B,73-FF,FF,FF.gif)
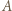 i
i 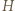 liczb
liczb ![x1, | ...,xn ∈[a,b].](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/3x-bed5f731d399079efabe3448810444f970457e80-im-66,57,43-FF,FF,FF.gif) Weźmy dowolną liczbę
Weźmy dowolną liczbę 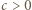 i zauważmy, że
i zauważmy, że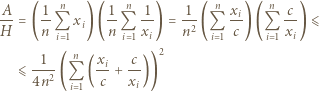
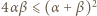 dla liczb
dla liczb 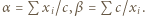
![x ∈ [a,b]](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/1x-2643bd4bae04ef39ab2c2805c88b5fc400e1fac5-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 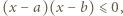 którą przepisujemy w postaci
którą przepisujemy w postaci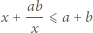
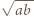 :
: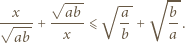
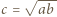 i korzystając z (2):
i korzystając z (2):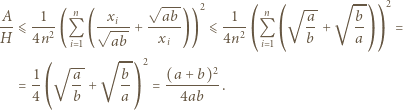
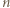 jest z założenia parzysta. Gdy
jest z założenia parzysta. Gdy 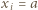 dla połowy spośród wskaźników
dla połowy spośród wskaźników 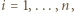 zaś
zaś 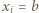 dla pozostałej połowy, wówczas we wszystkich szacowaniach zachodzi równość. Zatem liczba
dla pozostałej połowy, wówczas we wszystkich szacowaniach zachodzi równość. Zatem liczba 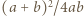 jest maksymalną wartością stosunku
jest maksymalną wartością stosunku 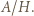
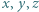 prawdziwa jest nierówność
prawdziwa jest nierówność
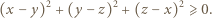

 i
i 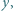 niebędących jednocześnie zerami.
niebędących jednocześnie zerami.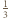 oraz
oraz 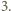 Rozwiązanie ułatwia spostrzeżenie, że szacowany ułamek ma dodatni licznik i mianownik, bo
Rozwiązanie ułatwia spostrzeżenie, że szacowany ułamek ma dodatni licznik i mianownik, bo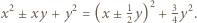
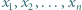 zachodzi nierówność
zachodzi nierówność
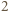 i przeniesieniu wszystkich wyrazów na lewą stronę nierówności otrzymamy
i przeniesieniu wszystkich wyrazów na lewą stronę nierówności otrzymamy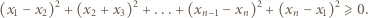

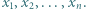
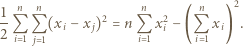
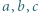 jest równa
jest równa 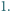 Udowodnić, że
Udowodnić, że
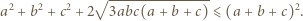
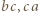 i
i 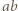 ułatwia dalsze rachunki.
ułatwia dalsze rachunki.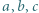 spełniają równość
spełniają równość 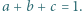 Wykazać, że
Wykazać, że
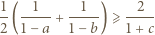
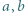 i
i  zachodzi nierówność
zachodzi nierówność
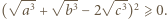
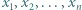 będą liczbami dodatnimi. Przyjmijmy
będą liczbami dodatnimi. Przyjmijmy 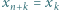 dla całkowitych
dla całkowitych 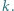 Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
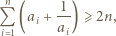
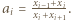
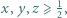 spełniających warunek
spełniających warunek 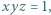 zachodzi nierówność
zachodzi nierówność
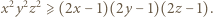
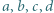 spełniają nierówność
spełniają nierówność