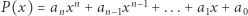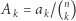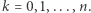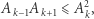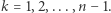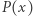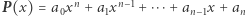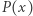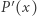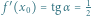Wielomiany, nierówności i Newton
Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...
I tak wielomian 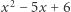 ma dwa pierwiastki rzeczywiste (
ma dwa pierwiastki rzeczywiste ( 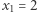 i
i 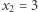 ), ale wielomian
), ale wielomian 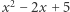 nie ma ani jednego. Twierdzenie Bézouta orzeka, że jeśli
nie ma ani jednego. Twierdzenie Bézouta orzeka, że jeśli 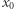 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 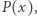 to możemy zapisać
to możemy zapisać 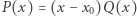 dla pewnego wielomianu
dla pewnego wielomianu 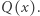 Jeśli dla liczby naturalnej
Jeśli dla liczby naturalnej 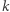 zachodzi
zachodzi 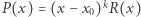 dla pewnego wielomianu
dla pewnego wielomianu 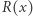 oraz
oraz 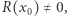 to mówimy, że
to mówimy, że 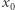 jest
jest 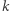 -krotnym pierwiastkiem wielomianu
-krotnym pierwiastkiem wielomianu 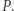 W tej sytuacji wielomian
W tej sytuacji wielomian 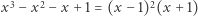 ma jeden pierwiastek dwukrotny i jeden pierwiastek jednokrotny. Z twierdzenia Bézouta można wywnioskować, że wielomian stopnia
ma jeden pierwiastek dwukrotny i jeden pierwiastek jednokrotny. Z twierdzenia Bézouta można wywnioskować, że wielomian stopnia 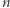 może mieć co najwyżej
może mieć co najwyżej 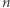 pierwiastków rzeczywistych (uwzględniając krotności). Jeśli ma ich dokładnie
pierwiastków rzeczywistych (uwzględniając krotności). Jeśli ma ich dokładnie 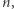 będziemy go nazywać najedzonym. Nie jest to formalny, matematyczny termin, jednak wydaje się dużo bardziej wdzięczny niż dokładne tłumaczenie angielskiego terminu real rooted. Rzecz jasna, wielomiany, które nie są najedzone, będziemy nazywać głodnymi.
będziemy go nazywać najedzonym. Nie jest to formalny, matematyczny termin, jednak wydaje się dużo bardziej wdzięczny niż dokładne tłumaczenie angielskiego terminu real rooted. Rzecz jasna, wielomiany, które nie są najedzone, będziemy nazywać głodnymi.
Czy można rozpoznać najedzony (lub głodny) wielomian "na pierwszy rzut oka"? Zacznijmy od wielomianów stopnia pierwszego - oczywiście każdy z nich jest najedzony. Wielomiany stopnia drugiego mogą być głodne (tak jak wspomniany wcześniej wielomian 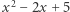 ), jednak po latach szkolnego treningu powinniśmy je bez trudu rozpoznać. Wszak jeśli trójmian kwadratowy
), jednak po latach szkolnego treningu powinniśmy je bez trudu rozpoznać. Wszak jeśli trójmian kwadratowy 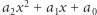 ma dwa pierwiastki rzeczywiste (czyli jest najedzony), to jego wyróżnik
ma dwa pierwiastki rzeczywiste (czyli jest najedzony), to jego wyróżnik 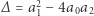 jest nieujemny, czyli
jest nieujemny, czyli 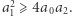 Widać zatem, że poczucie sytości u wielomianu może być związane z pewnymi nierównościami dotyczącymi jego współczynników. Celem artykułu jest przedstawienie uogólnienia wspomnianej przed chwilą własności trójmianu kwadratowego na wielomiany większych stopni. Wyraża je następujące twierdzenie:
Widać zatem, że poczucie sytości u wielomianu może być związane z pewnymi nierównościami dotyczącymi jego współczynników. Celem artykułu jest przedstawienie uogólnienia wspomnianej przed chwilą własności trójmianu kwadratowego na wielomiany większych stopni. Wyraża je następujące twierdzenie:
Aby udowodnić powyższe twierdzenie, potrzebujemy najpierw przyjrzeć się dokładniej najedzonym wielomianom. Dla wygody, w dalszej części artykułu przyjmijmy oznaczenia takie jak w treści twierdzenia. Istotne będą dla nas pewne dwie operacje, które możemy przeprowadzić na najedzonym wielomianie, tak aby nie zgłodniał. Pierwsza z nich to "lustrzane odbicie":
Żeby przekonać się o słuszności faktu 1, musimy przyjrzeć się, czy i jak zmieniają się pierwiastki i ich krotności, gdy stosujemy "lustrzane odbicie". Zwróćmy uwagę, że skoro 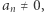 to 0 nie może być pierwiastkiem wielomianu
to 0 nie może być pierwiastkiem wielomianu 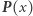 (jego wyraz wolny jest niezerowy). Załóżmy, że 0 jest
(jego wyraz wolny jest niezerowy). Załóżmy, że 0 jest 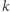 -krotnym pierwiastkiem wielomianu
-krotnym pierwiastkiem wielomianu 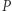 (jeśli 0 nie jest pierwiastkiem
(jeśli 0 nie jest pierwiastkiem 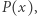 przyjmijmy
przyjmijmy 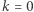 ). Wówczas
). Wówczas 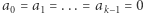 i
i 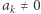 (a jeśli
(a jeśli  nie bierzemy pod uwagę pierwszego ciągu równości). W tej sytuacji wielomian
nie bierzemy pod uwagę pierwszego ciągu równości). W tej sytuacji wielomian  ma stopień
ma stopień 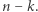 Załóżmy teraz, że
Załóżmy teraz, że 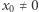 jest
jest 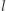 -krotnym pierwiastkiem wielomianu
-krotnym pierwiastkiem wielomianu  i niech
i niech 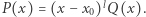 Nietrudno uzasadnić, że dla dowolnego
Nietrudno uzasadnić, że dla dowolnego 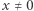 zachodzi
zachodzi 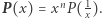 W tej sytuacji proste przekształcenia algebraiczne prowadzą do wniosku, że
W tej sytuacji proste przekształcenia algebraiczne prowadzą do wniosku, że
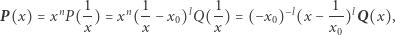 |
gdzie 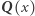 jest "lustrzanym odbiciem" wielomianu
jest "lustrzanym odbiciem" wielomianu 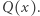 Ponieważ
Ponieważ 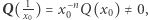 powyższa równość dowodzi, że
powyższa równość dowodzi, że 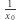 jest
jest 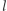 -krotnym pierwiastkiem wielomianu
-krotnym pierwiastkiem wielomianu 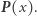 Przedstawione rozważania dowodzą, że wielomian
Przedstawione rozważania dowodzą, że wielomian 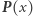 jest najedzony, gdyż krotności odwrotności niezerowych pierwiastków wielomianu
jest najedzony, gdyż krotności odwrotności niezerowych pierwiastków wielomianu 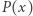 sumują się do
sumują się do 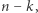 czyli stopnia wielomianu
czyli stopnia wielomianu 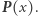
Druga operacja niepowodująca głodu, która będzie nam potrzebna, to różniczkowanie wielomianu. Czytelnikom, którzy nie znają różniczkowania, polecamy przeczytać krótką notkę na końcu artykułu.
Powyższy fakt wynika stąd, że różniczkowanie obniża krotność każdego pierwiastka o 1, w związku z czym wyjściowy wielomian "traci" przy różniczkowaniu 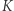 pierwiastków, gdzie
pierwiastków, gdzie 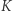 jest liczbą różnych jego pierwiastków. Z drugiej strony, na mocy twierdzenia Rolle'a, między dwoma sąsiednimi (na osi liczb rzeczywistych) pierwiastkami wielomianu
jest liczbą różnych jego pierwiastków. Z drugiej strony, na mocy twierdzenia Rolle'a, między dwoma sąsiednimi (na osi liczb rzeczywistych) pierwiastkami wielomianu 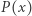 istnieje pierwiastek wielomianu
istnieje pierwiastek wielomianu 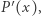 i w ten sposób wielomian
i w ten sposób wielomian 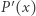 "zyskuje"
"zyskuje" 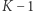 nowych pierwiastków. Uwzględniając te dwie obserwacje, potrafimy zlokalizować
nowych pierwiastków. Uwzględniając te dwie obserwacje, potrafimy zlokalizować 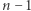 (gdzie
(gdzie  to stopień wielomianu
to stopień wielomianu 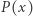 ) pierwiastków
) pierwiastków 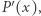 licząc krotności. Ponieważ stopień
licząc krotności. Ponieważ stopień 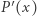 również wynosi
również wynosi  jest on najedzony.
jest on najedzony.
Uzbrojeni w fakty 1 i 2 możemy przejść do dowodu twierdzenia. Załóżmy, że wielomian 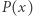 jest najedzony, i wybierzmy dowolnie
jest najedzony, i wybierzmy dowolnie 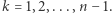 Ponieważ różniczkowanie nie sprawia, że wielomian staje się głodny, to stosując tę operację
Ponieważ różniczkowanie nie sprawia, że wielomian staje się głodny, to stosując tę operację 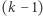 razy na wielomianie
razy na wielomianie  otrzymamy wielomian
otrzymamy wielomian
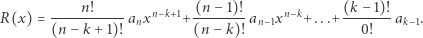 |
Ponieważ wielomian  jest najedzony, to jego lustrzane odbicie
jest najedzony, to jego lustrzane odbicie
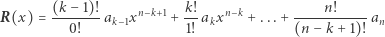 |
także jest najedzone. W tej sytuacji różniczkując 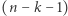 razy wielomian
razy wielomian 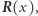 dostaniemy najedzony wielomian
dostaniemy najedzony wielomian
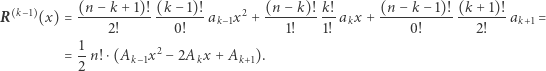
Oznacza to, że wielomian 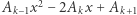 również jest najedzony, jednak zgodnie z informacjami przedstawionymi we wstępie do tego artykułu oznacza to, że
również jest najedzony, jednak zgodnie z informacjami przedstawionymi we wstępie do tego artykułu oznacza to, że 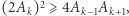 co jest równoważne (*) i kończy dowód.
co jest równoważne (*) i kończy dowód.
Nierówności (*) noszą nazwę nierówności Newtona, gdyż Isaac Newton w swoim dziele Arithmetica Universalis (1707) stwierdził (bez dowodu), że liczba rzeczywistych pierwiastków wielomianu 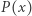 jest nie mniejsza od stopnia wielomianu pomniejszonego o liczbę zmian znaku w ciągu
jest nie mniejsza od stopnia wielomianu pomniejszonego o liczbę zmian znaku w ciągu
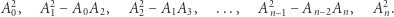 |
Nietrudno przekonać się, że przedstawiona hipoteza jest silniejsza od naszego twierdzenia, jednak na swój dowód czekała ponad 100 lat. Udowodnił ją James Sylvester w roku 1865.
Nasze twierdzenie nie musiało być aż tak cierpliwe, gdyż wykazał je w roku 1729 uczeń Newtona, Colin Maclaurin, próbując uzasadnić hipotezę postawioną przez nauczyciela. Zauważył on również, że jeśli wielomian 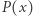 jest najedzony,
jest najedzony, 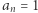 i liczby
i liczby 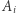 są dodatnie, to zachodzi
są dodatnie, to zachodzi
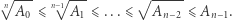 |
Są to tak zwane nierówności Maclaurina. Ich uzasadnienie jest następujące: przy poczynionych założeniach dla dowolnego  mamy
mamy
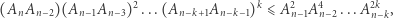 |
co po skróceniu przez 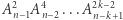 daje
daje 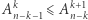 i ostatecznie
i ostatecznie 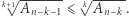
Przypomnijmy teraz wzory Viète'a: jeśli 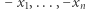 są pierwiastkami wielomianu
są pierwiastkami wielomianu 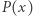 i
i 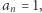 to
to
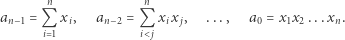 |
Jeśli wszystkie liczby 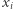 są dodatnie, to spełnione są założenia dla nierówności Maclaurina. Zwróćmy uwagę, że wówczas
są dodatnie, to spełnione są założenia dla nierówności Maclaurina. Zwróćmy uwagę, że wówczas
 |
W tej sytuacji nierówność Maclaurina stanowi uogólnienie dobrze znanej nierówności między średnią geometryczną a arytmetyczną. Warto zwrócić uwagę, że popularny dowód tej nierówności poprzez zastosowanie indukcji wstecznej pochodzi od matematyka Augustina Cauchy'ego i został opublikowany dopiero w 1827 roku. Czytelnikom, którzy nie są zaznajomieni z tym pięknym rozumowaniem, polecamy artykuł Indukcja wsteczna z Delty 2/2011.
Na zakończenie warto zaznaczyć, że przedstawione twierdzenie nie charakteryzuje najedzonych wielomianów. Dla przykładu, wielomian 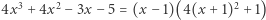 nie jest najedzony, ale spełnia opisane przez (*) nierówności. Czy w ogóle istnieją takie charakteryzacje? I tak i nie, ale to już inna, dłuższa historia.
nie jest najedzony, ale spełnia opisane przez (*) nierówności. Czy w ogóle istnieją takie charakteryzacje? I tak i nie, ale to już inna, dłuższa historia.
O różniczkowaniu dla nieróżniczkujących.
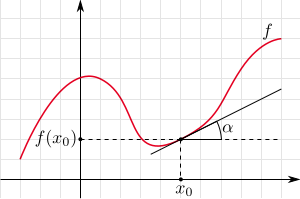
Ze względu na młodszych Czytelników Delty poniżej prezentujemy krótką "bajkę" o tym, czym to różniczkowanie jest. Niech 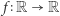 będzie pewną funkcją. Jeśli istnieje prosta styczna do wykresu funkcji
będzie pewną funkcją. Jeśli istnieje prosta styczna do wykresu funkcji  w pewnym punkcie
w pewnym punkcie 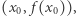 to tangens kąta nachylenia tej stycznej nazwiemy pochodną funkcji
to tangens kąta nachylenia tej stycznej nazwiemy pochodną funkcji  w punkcie
w punkcie  i będziemy oznaczać przez
i będziemy oznaczać przez 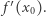 W szczególności, jeśli
W szczególności, jeśli 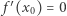 dla pewnego
dla pewnego 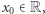 to styczna do wykresu funkcji
to styczna do wykresu funkcji 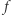 w punkcie
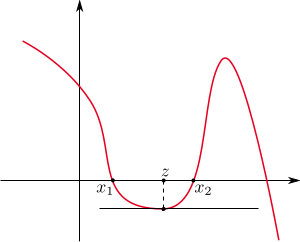
w punkcie 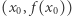 jest pozioma. Łatwo w związku z tym uwierzyć, że jeśli dla pewnych
jest pozioma. Łatwo w związku z tym uwierzyć, że jeśli dla pewnych 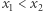 mamy
mamy  oraz w każdym punkcie przedziału
oraz w każdym punkcie przedziału ![|[x1,x2]](/math/temat/matematyka/algebra/2020/09/29/wielomiany-nierownosci-i-newton/13x-2f02637a10791467c4af5232d4c98048894ca0f1-im-33,33,33-FF,FF,FF.gif) istnieje styczna do wykresu funkcji
istnieje styczna do wykresu funkcji  to w pewnym punkcie ta styczna jest pozioma, czyli istnieje
to w pewnym punkcie ta styczna jest pozioma, czyli istnieje 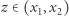 takie, że
takie, że  Mówi o tym twierdzenie Rolle'a.
Mówi o tym twierdzenie Rolle'a.
Okazuje się, że pochodna wielomianu 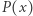 wyraża się wzorem
wyraża się wzorem 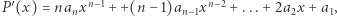 czego nie będziemy tutaj dowodzić. Jeśli
czego nie będziemy tutaj dowodzić. Jeśli  i
i 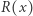 są wielomianami, można algebraicznie udowodnić następującą równość, co polecamy jako ćwiczenie:
są wielomianami, można algebraicznie udowodnić następującą równość, co polecamy jako ćwiczenie:
 |
Równość ta jest słuszna nie tylko dla wielomianów, ale w ogólnym przypadku dowód już nie jest algebraiczny. Kolejnym ćwiczeniem jest uzasadnienie, jak z powyższej równości wynika fakt, że jeśli  jest
jest 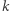 -krotnym pierwiastkiem wielomianu
-krotnym pierwiastkiem wielomianu  to jest
to jest 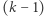 -krotnym pierwiastkiem wielomianu
-krotnym pierwiastkiem wielomianu