Problem Parzystkowa i jego uogólnienia
W mieście Parzystkowo zacny burmistrz postanowił w nietypowy sposób zaktywizować społeczeństwo. Zarządził utworzenie stowarzyszeń, które wykonywać będą powierzone im zadania...
W trakcie zebrania z Radą Miasta uchwalono następujące zasady:
- 1.
- każde stowarzyszenie wyznaczone jest jednoznacznie przez swój skład (innymi słowy nie ma dwóch stowarzyszeń o takim samym składzie osobowym),
- 2.
- każde stowarzyszenie ma parzystą liczbę uczestników,
- 3.
- część wspólna każdych dwóch stowarzyszeń tworzy ugrupowanie złożone z parzystej liczby uczestników.
Rada rada, burmistrz zadowolony... A mieszkańcy? Bardzo chętni do dzielenia się na stowarzyszenia. Okazało się jednak, że to, co łatwe w teorii, w praktyce może być trudne. Powstał bowiem niemały chaos - tym większy, im więcej stowarzyszeń już zostało powołanych. Wszystko dlatego, że mieszkańcy chcieli utworzyć ich jak najwięcej. Zbadajmy tę sprawę.
Opisany powyżej problem zwany problemem Parzystkowa (Eventown problem) można sformułować następująco. Niech 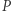 będzie zbiorem
będzie zbiorem 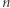 -elementowym oraz niech
-elementowym oraz niech 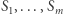 będą jego podzbiorami. Żądamy od tych podzbiorów, żeby:
będą jego podzbiorami. Żądamy od tych podzbiorów, żeby:
- 1.
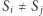 dla
dla 
- 2.
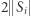 dla dowolnego
dla dowolnego 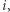
- 3.
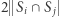 dla
dla 
gdzie 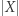 oznacza liczbę elementów zbioru
oznacza liczbę elementów zbioru 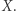 Zachodzi następujące oszacowanie na liczbę ugrupowań.
Zachodzi następujące oszacowanie na liczbę ugrupowań.

Twierdzenie 1. Maksymalna liczba stowarzyszeń w Parzystkowie liczącym 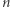 mieszkańców wynosi co najmniej
mieszkańców wynosi co najmniej 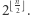
Dowód jest prosty i konstruktywny.
Dowód. Załóżmy na początek, że 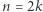 dla pewnego
dla pewnego 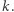 Dzielimy zbiór
Dzielimy zbiór 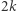 -elementowy na
-elementowy na 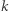 różnych podzbiorów 2-elementowych. Każde stowarzyszenie budujemy teraz z tych par (rysunek obok). Jak widać, takie stowarzyszenia spełniają wszystkie postulowane warunki.
różnych podzbiorów 2-elementowych. Każde stowarzyszenie budujemy teraz z tych par (rysunek obok). Jak widać, takie stowarzyszenia spełniają wszystkie postulowane warunki.
Ponieważ par jest 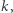 wszystkich podzbiorów jest
wszystkich podzbiorów jest 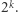 Znaleźliśmy zatem
Znaleźliśmy zatem 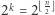 stowarzyszeń, co kończy dowód w przypadku
stowarzyszeń, co kończy dowód w przypadku 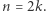 Jeśli teraz
Jeśli teraz 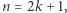 to odsuwamy na bok jednego mieszkańca i rozważamy problem dla parzystej liczby mieszkańców, otrzymując
to odsuwamy na bok jednego mieszkańca i rozważamy problem dla parzystej liczby mieszkańców, otrzymując 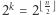 stowarzyszeń.
stowarzyszeń.
Zauważamy, że próba manipulowania parami nie prowadzi do utworzenia nowego stowarzyszenia ponad te zdefiniowane przez podzbiory par. Okazuje się ponadto, że jest to najlepszy możliwy podział - nierówność w twierdzeniu 1 można zastąpić równością.
Niełatwy dowód tego twierdzenia pomijamy. Oryginalny problem Parzystkowa można oczywiście modyfikować. Niech 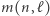 oznacza maksymalną liczbę stowarzyszeń w mieście o
oznacza maksymalną liczbę stowarzyszeń w mieście o 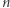 mieszkańcach, przy następujących zasadach:
mieszkańcach, przy następujących zasadach:
- (1)
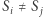 dla
dla 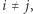
- (2)
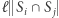 dla
dla 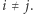
Zauważmy, że można podzielić mieszkańców na zbiory złożone z 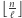 osób i rozważyć stowarzyszenia jako podzbiory tych grup (tak jak w Parzystkowie). Wynika z tego następujące oszacowanie.
osób i rozważyć stowarzyszenia jako podzbiory tych grup (tak jak w Parzystkowie). Wynika z tego następujące oszacowanie.
Powyższe szacowanie jest elementarne, jednak nie jest znane ogólne, dokładne rozwiązanie.
Problem Nieparzystkowa
Pokażemy teraz, że w pewnych sytuacjach potrafimy podać dokładną odpowiedź. Rozważmy problem miasta Nieparzystkowo:
- 1.
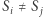 dla
dla 
- 2.
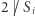 dla dowolnego
dla dowolnego 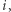
- 3.
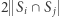 dla
dla 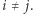
Ponownie pytamy o maksymalną liczbę stowarzyszeń. Zaczniemy tym razem od podania górnego szacowania. Niech  będzie ciałem o
będzie ciałem o 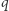 -elementach. Zbiór
-elementach. Zbiór 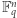 to zbiór wektorów
to zbiór wektorów 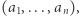 gdzie każde
gdzie każde 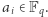 W tym zbiorze naturalnym działaniem jest dodawanie wektorów po współrzędnych. Możemy również rozważyć działanie mnożenia liczby przez wektor. To znaczy jeśli
W tym zbiorze naturalnym działaniem jest dodawanie wektorów po współrzędnych. Możemy również rozważyć działanie mnożenia liczby przez wektor. To znaczy jeśli 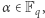 to
to
 |
Powiemy, że wektory 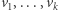 są liniowo niezależne w
są liniowo niezależne w  jeśli układ równań
jeśli układ równań
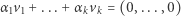 |
ma dokładnie jedno rozwiązanie 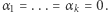 W
W 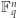 możemy również rozważyć iloczyn skalarny dwóch wektorów
możemy również rozważyć iloczyn skalarny dwóch wektorów 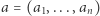 oraz
oraz 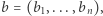 to jest liczbę
to jest liczbę
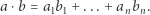 |
Zauważmy, że jeżeli wśród wektorów 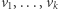 są dwa wektory równe lub jeden z wektorów jest złożony z samych zer, to wektory te nie są liniowo niezależne.
są dwa wektory równe lub jeden z wektorów jest złożony z samych zer, to wektory te nie są liniowo niezależne.
Dowód. Zauważmy, że każdy wektor 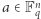 można zapisać jednoznacznie jako
można zapisać jednoznacznie jako  gdzie w wektorze
gdzie w wektorze  na
na 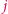 -tym miejscu stoi 1, na pozostałych zaś 0. W szczególności wektory
-tym miejscu stoi 1, na pozostałych zaś 0. W szczególności wektory  są liniowo niezależne. Pokażemy teraz, że żaden inny układ wektorów liniowo niezależnych nie może być liczniejszy niż
są liniowo niezależne. Pokażemy teraz, że żaden inny układ wektorów liniowo niezależnych nie może być liczniejszy niż 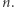
Załóżmy, że 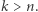 Z uczynionej przed chwilą uwagi każdy z
Z uczynionej przed chwilą uwagi każdy z 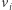 można zapisać jako sumę
można zapisać jako sumę 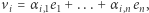 wiemy w szczególności, że
wiemy w szczególności, że 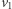 także można. Załóżmy teraz bez straty ogólności, że
także można. Załóżmy teraz bez straty ogólności, że 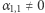 (gdyby tak nie było, to wystarczy przenumerować wektory
(gdyby tak nie było, to wystarczy przenumerować wektory 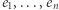 do otrzymania żądanej cechy). Wtedy również
do otrzymania żądanej cechy). Wtedy również
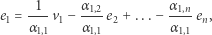 |
zatem każdy wektor, który można zapisać jako kombinację wektorów 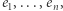 można również zapisać jako kombinację wektorów
można również zapisać jako kombinację wektorów 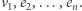 W szczególności
W szczególności 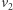 można tak zapisać. Zauważmy, że przynajmniej jeden ze współczynników stojących przy
można tak zapisać. Zauważmy, że przynajmniej jeden ze współczynników stojących przy 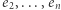 w zapisie
w zapisie 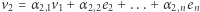 jest niezerowy; w przeciwnym przypadku
jest niezerowy; w przeciwnym przypadku 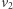 byłby liniowo zależny od
byłby liniowo zależny od 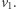 Podobnie jak poprzednio, można założyć, że
Podobnie jak poprzednio, można założyć, że 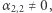 oraz uzasadnić, że każdy wektor, który jest kombinacją wektorów
oraz uzasadnić, że każdy wektor, który jest kombinacją wektorów  jest też kombinacją wektorów
jest też kombinacją wektorów 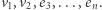
Postępując analogicznie jak powyżej dla 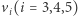 dochodzimy do momentu, w którym wszystkie wektory
dochodzimy do momentu, w którym wszystkie wektory 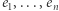 zastąpiliśmy przez
zastąpiliśmy przez 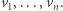 Ponieważ założyliśmy, że
Ponieważ założyliśmy, że 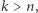 zatem wektor
zatem wektor 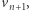 który potrafimy zapisać za pomocą wektorów
który potrafimy zapisać za pomocą wektorów 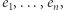 potrafimy również zapisać za pomocą wektorów
potrafimy również zapisać za pomocą wektorów 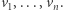 Jest to jednak sprzeczne z liniową niezależnością wektorów.
Jest to jednak sprzeczne z liniową niezależnością wektorów.
Otrzymana powyżej sprzeczność oznacza, że warunek 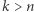 jest niemożliwy do spełnienia.
jest niemożliwy do spełnienia.
Dowód. Rozważmy zbiór  Każde stowarzyszenie
Każde stowarzyszenie 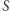 reprezentujemy przez jego wektor charakterystyczny
reprezentujemy przez jego wektor charakterystyczny 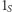 w
w 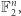 to jest taki wektor, w którym jeśli
to jest taki wektor, w którym jeśli 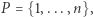 to
to 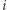 -ta współrzędna wektora
-ta współrzędna wektora 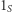 jest równa 1 wtedy i tylko wtedy, gdy
jest równa 1 wtedy i tylko wtedy, gdy 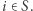 W przeciwnym przypadku
W przeciwnym przypadku  -ta współrzędna jest równa 0. Powiedzmy, że tych wektorów jest
-ta współrzędna jest równa 0. Powiedzmy, że tych wektorów jest 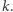
Wektory postaci 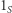 są liniowo niezależne. Aby to uzasadnić, załóżmy, że
są liniowo niezależne. Aby to uzasadnić, załóżmy, że
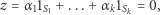 |
i rozważmy iloczyn skalarny 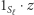 dla pewnego
dla pewnego 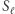 (dowolnego;
(dowolnego;  ). Zauważmy, że:
). Zauważmy, że:
 (liczba członków stowarzyszenia jest nieparzysta) - iloczyn skalarny obliczamy modulo 2 (patrz tabele na marginesie),
(liczba członków stowarzyszenia jest nieparzysta) - iloczyn skalarny obliczamy modulo 2 (patrz tabele na marginesie),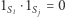 dla
dla 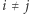 (część wspólna stowarzyszeń jest parzysta).
(część wspólna stowarzyszeń jest parzysta).
Wynika z tego, że
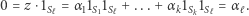 |
Rozważając kolejne 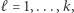 otrzymujemy
otrzymujemy 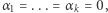 a więc wektory
a więc wektory 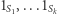 są liniowo niezależne. Z lematu wynika teraz, że
są liniowo niezależne. Z lematu wynika teraz, że 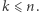
Ostatni krok to pokazanie, że można utworzyć dokładnie 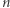 stowarzyszeń. W tym celu wystarczy, aby każde stowarzyszenie złożone było z jednego mieszkańca.
stowarzyszeń. W tym celu wystarczy, aby każde stowarzyszenie złożone było z jednego mieszkańca.
Na zakończenie
Wróćmy do ogólnego problemu. Jak już wspomnieliśmy, nie istnieje ogólny wzór na 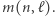 W twierdzeniu 3 wskazane zostało dolne oszacowanie. Ciekawe natomiast jest także znalezienie szacowania górnego. Wskazujemy je w poniższym twierdzeniu.
W twierdzeniu 3 wskazane zostało dolne oszacowanie. Ciekawe natomiast jest także znalezienie szacowania górnego. Wskazujemy je w poniższym twierdzeniu.
Twierdzenie 5. Zachodzą nierówności:
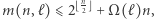 gdzie
gdzie 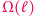 jest krotnością czynników pierwszych w rozkładzie liczby
jest krotnością czynników pierwszych w rozkładzie liczby 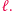
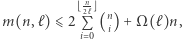
- dla
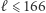 zachodzi
zachodzi 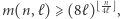
- dla
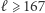 zachodzi
zachodzi 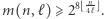
Ciekawostką jest fakt, że w dowodzie trzeciego z powyższych oszacowań wykorzystuje się tak zwane macierze Hadamarda (macierze kwadratowe o wymiarze 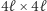 o tej własności, że ich wyrazami są tylko 1 oraz -1 i iloczyny skalarne wszystkich możliwych par wierszy są równe 0). Wiadomo, że takie macierze istnieją dla wszystkich
o tej własności, że ich wyrazami są tylko 1 oraz -1 i iloczyny skalarne wszystkich możliwych par wierszy są równe 0). Wiadomo, że takie macierze istnieją dla wszystkich 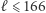 oraz dla wszystkich liczb postaci
oraz dla wszystkich liczb postaci 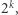 gdzie
gdzie 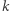 jest dodatnią liczbą naturalną.
jest dodatnią liczbą naturalną.
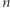
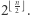
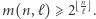
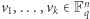
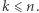
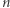
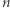
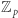 - zbiór liczb od 0 do
- zbiór liczb od 0 do 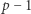 z działaniami dodawania i mnożenia liczb całkowitych modulo
z działaniami dodawania i mnożenia liczb całkowitych modulo