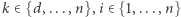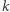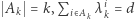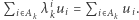Podróże w 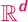
... Uważam, że jednostronnicowy dowód Sergeya Sevastianova jest wyjątkowy. Pál Erdős często odwoływał się do Księgi, w której Bóg trzyma wszystkie najelegantsze dowody. Zainspirowani tym matematycy, Aigner i Ziegler, wydali znakomitą książkę Dowody z Księgi, którą wszystkim szczerze polecam. Dowód Sevastianova mógłby również trafić do tej Księgi. Mimo że ja i moi koledzy rozumiemy każdy krok tego dowodu z osobna, to nie wiemy, skąd bierze się taki sposób rozumowania, niespotykany nigdzie indziej w naszej dziedzinie. Wierzę, że zrozumienie idei ukrytych w tym dowodzie może przyczynić się do kolejnych ciekawych wyników. Kto wie, może ktoś z Czytelników pomoże?
Rozważmy następujący problem. Mamy danych wiele 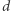 -wymiarowych wektorów:
-wymiarowych wektorów: 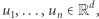 takich że sumują się one do wektora zerowego, czyli
takich że sumują się one do wektora zerowego, czyli 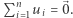 Podkreślmy, że liczba wektorów
Podkreślmy, że liczba wektorów  może być dużo większa niż
może być dużo większa niż  Załóżmy dodatkowo, że długości wszystkich wektorów
Załóżmy dodatkowo, że długości wszystkich wektorów 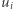 są nie większe niż 1. Dla danego ciągu wektorów
są nie większe niż 1. Dla danego ciągu wektorów 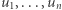 rozważmy podróż tym ciągiem w przestrzeni
rozważmy podróż tym ciągiem w przestrzeni  w której startujemy z zera
w której startujemy z zera 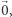 a potem kolejno przesuwamy się o
a potem kolejno przesuwamy się o 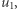 o
o  o
o  itd., a na końcu o
itd., a na końcu o  Oczywiście na koniec całej podróży wrócimy do zera, ale w międzyczasie możemy od tego zera odsunąć się bardzo daleko. Pytanie brzmi, czy dla dowolnych wektorów
Oczywiście na koniec całej podróży wrócimy do zera, ale w międzyczasie możemy od tego zera odsunąć się bardzo daleko. Pytanie brzmi, czy dla dowolnych wektorów 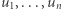 istnieje takie ich poprzestawianie, inaczej permutacja
istnieje takie ich poprzestawianie, inaczej permutacja 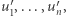 żeby podróż tym ciągiem wektorów nigdy nie oddalała się znacząco od zera. Mówiąc bardziej precyzyjnie, czy dla dowolnego wymiaru
żeby podróż tym ciągiem wektorów nigdy nie oddalała się znacząco od zera. Mówiąc bardziej precyzyjnie, czy dla dowolnego wymiaru 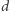 istnieje taka stała
istnieje taka stała 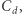 że dla dowolnego ciągu wektorów
że dla dowolnego ciągu wektorów 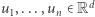 nie dłuższych niż 1 i sumujących się do
nie dłuższych niż 1 i sumujących się do  istnieje ich permutacja
istnieje ich permutacja 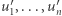 taka, że dla dowolnego
taka, że dla dowolnego 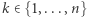 zachodzi
zachodzi 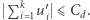 Nim przejdziemy do rozwiązania, zachęcam Ambitnego Czytelnika do samodzielnej próby odpowiedzenia na to pytanie albo przynajmniej postawienia hipotezy i obstawienia ewentualnej wartości
Nim przejdziemy do rozwiązania, zachęcam Ambitnego Czytelnika do samodzielnej próby odpowiedzenia na to pytanie albo przynajmniej postawienia hipotezy i obstawienia ewentualnej wartości 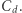
Dla wymiaru 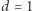 stosunkowo łatwo jest wykazać, że
stosunkowo łatwo jest wykazać, że 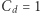 wystarczy. Konstruujemy ciąg wektorów
wystarczy. Konstruujemy ciąg wektorów 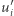 tak, żeby wartość bezwzględna
tak, żeby wartość bezwzględna 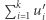 nigdy nie przekroczyła 1. Postępujemy w następujący sposób. Zaczynamy od ciągu pustego. Powiedzmy, że skonstruowaliśmy już ciąg
nigdy nie przekroczyła 1. Postępujemy w następujący sposób. Zaczynamy od ciągu pustego. Powiedzmy, że skonstruowaliśmy już ciąg  który spełnia nasze warunki dla początkowych wyrazów. Załóżmy bez straty ogólności, że
który spełnia nasze warunki dla początkowych wyrazów. Załóżmy bez straty ogólności, że  Skoro suma wszystkich wektorów
Skoro suma wszystkich wektorów 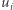 wynosi 0, a suma wektorów już wybranych do ciągu jest nieujemna, to suma wektorów niewybranych jest niedodatnia. A więc istnieje tam jakiś wektor niedodatni, tego właśnie wybieramy jako
wynosi 0, a suma wektorów już wybranych do ciągu jest nieujemna, to suma wektorów niewybranych jest niedodatnia. A więc istnieje tam jakiś wektor niedodatni, tego właśnie wybieramy jako 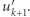 Postępując w ten sposób do końca, otrzymamy ciąg o wymaganych własnościach. Łatwo też zauważyć, że
Postępując w ten sposób do końca, otrzymamy ciąg o wymaganych własnościach. Łatwo też zauważyć, że 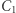 jest wybrana optymalnie, ciąg
jest wybrana optymalnie, ciąg 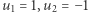 nie da się ułożyć lepiej.
nie da się ułożyć lepiej.
Dla wyższych wymiarów sprawa nie jest tak oczywista i mimo bardzo prostego sformułowania ma za sobą długą historię badań. Już w roku 1914 niemiecki matematyk Ernst Steinitz (znany m.in. z twierdzenia o dopełnianiu zbioru liniowo niezależnych wektorów do bazy) udowodnił, że dla dowolnego  stała
stała  spełnia zadane warunki. Dlatego wspomniany fakt zwany jest lematem Steinitza. Sytuacja staje się jednak ciekawsza, gdy rozważymy inne, nieco dziwniejsze sposoby mierzenia wielkości wektora. Takie funkcje, przyporządkowujące wektorowi z
spełnia zadane warunki. Dlatego wspomniany fakt zwany jest lematem Steinitza. Sytuacja staje się jednak ciekawsza, gdy rozważymy inne, nieco dziwniejsze sposoby mierzenia wielkości wektora. Takie funkcje, przyporządkowujące wektorowi z 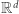 liczbę mierzącą w pewien rozsądny sposób jego wielkość, zwane są normami. Popularne przykłady norm to: długość wektora (zwana normą euklidesową), suma wartości bezwzględnych jego współrzędnych czy też maksymalna wartość bezwzględna jego współrzędnych (zwana normą maksimum), ale istnieją też inne, bardziej wymyślne normy. W ogólności norma to funkcja przyporządkowująca wektorowi
liczbę mierzącą w pewien rozsądny sposób jego wielkość, zwane są normami. Popularne przykłady norm to: długość wektora (zwana normą euklidesową), suma wartości bezwzględnych jego współrzędnych czy też maksymalna wartość bezwzględna jego współrzędnych (zwana normą maksimum), ale istnieją też inne, bardziej wymyślne normy. W ogólności norma to funkcja przyporządkowująca wektorowi 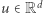 wartość
wartość 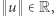 spełniająca trzy proste warunki:
spełniająca trzy proste warunki:
- 1)
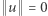 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy  to wektor zerowy,
to wektor zerowy,- 2)
- norma skaluje się liniowo, czyli
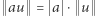 dla dowolnego
dla dowolnego 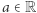 oraz
oraz 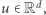
- 3)
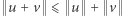 dla dowolnych
dla dowolnych 
Z faktu, że dla normy euklidesowej 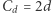 wystarcza, wynika łatwo, że dla dowolnej normy taka stała
wystarcza, wynika łatwo, że dla dowolnej normy taka stała 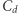 istnieje, nie wynika jednak w żaden sposób, jak duża jest ta stała. W roku 1931 Borgström wykazał, że dla dowolnej normy optymalna stała
istnieje, nie wynika jednak w żaden sposób, jak duża jest ta stała. W roku 1931 Borgström wykazał, że dla dowolnej normy optymalna stała 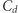 jest nie większa niż
jest nie większa niż  Aż do roku 1978 najlepsza znana stała
Aż do roku 1978 najlepsza znana stała  wciąż była wykładnicza względem
wciąż była wykładnicza względem 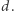 Dopiero wtedy, w 1978 roku, Sergey Sevastianov opublikował w rosyjskim czasopiśmie w Nowosybirsku dowód uzasadniający, że dla dowolnej normy
Dopiero wtedy, w 1978 roku, Sergey Sevastianov opublikował w rosyjskim czasopiśmie w Nowosybirsku dowód uzasadniający, że dla dowolnej normy 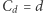 wystarczy. Praca miała dwie strony, przy czym dowód głównego wyniku zajmował w zasadzie jedną stronę, co jest oczywiście nadzwyczajne w wypadku rozwiązania znanego problemu tak długo otwartego. Przetłumaczoną na angielski wersję można znaleźć, wpisując w wyszukiwarce Google frazę "Value of the Steinitz constant". Mniej więcej rok lub dwa lata temu artykuł ten wpadł mi w ręce, ponieważ wynik jest związany z moimi zainteresowaniami naukowymi. Uważam, że dowód jest wyjątkowy. Pál Erdős, jeden z najwybitniejszych matematyków XX wieku często odwoływał się do Księgi, w której Bóg trzyma wszystkie najelegantsze dowody twierdzeń matematycznych. Zainspirowani tym powiedzeniem dwaj matematycy, Eigner i Ziegler, wydali znakomitą książkę "Dowody z Księgi", którą szczerze polecam każdemu Czytelnikowi. Dowód, o którym mówię, być może również mógłby trafić do takiej Księgi. Mimo że ja i moi koledzy rozumiemy każdy krok tego dowodu z osobna, to nie wiemy, skąd bierze się taki sposób rozumowania, niespotykany nigdzie indziej w naszej dziedzinie. Wydaje się, że za tym rozumowaniem stoi pewna intuicja geometryczna, ale nie wiemy, jaka to jest intuicja. Wierzę, że dogłębne zrozumienie idei ukrytych w tym dowodzie może przyczynić się do kolejnych ciekawych wyników. Kto wie, może ktoś z Czytelników pomoże?
wystarczy. Praca miała dwie strony, przy czym dowód głównego wyniku zajmował w zasadzie jedną stronę, co jest oczywiście nadzwyczajne w wypadku rozwiązania znanego problemu tak długo otwartego. Przetłumaczoną na angielski wersję można znaleźć, wpisując w wyszukiwarce Google frazę "Value of the Steinitz constant". Mniej więcej rok lub dwa lata temu artykuł ten wpadł mi w ręce, ponieważ wynik jest związany z moimi zainteresowaniami naukowymi. Uważam, że dowód jest wyjątkowy. Pál Erdős, jeden z najwybitniejszych matematyków XX wieku często odwoływał się do Księgi, w której Bóg trzyma wszystkie najelegantsze dowody twierdzeń matematycznych. Zainspirowani tym powiedzeniem dwaj matematycy, Eigner i Ziegler, wydali znakomitą książkę "Dowody z Księgi", którą szczerze polecam każdemu Czytelnikowi. Dowód, o którym mówię, być może również mógłby trafić do takiej Księgi. Mimo że ja i moi koledzy rozumiemy każdy krok tego dowodu z osobna, to nie wiemy, skąd bierze się taki sposób rozumowania, niespotykany nigdzie indziej w naszej dziedzinie. Wydaje się, że za tym rozumowaniem stoi pewna intuicja geometryczna, ale nie wiemy, jaka to jest intuicja. Wierzę, że dogłębne zrozumienie idei ukrytych w tym dowodzie może przyczynić się do kolejnych ciekawych wyników. Kto wie, może ktoś z Czytelników pomoże?
Przedstawiam dowód z oryginalnej pracy Sevastianova nieco przeze mnie zmodyfikowany. Poniżej ustalamy dowolnie wybraną normę wektora 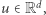 którą oznaczamy
którą oznaczamy  Przypomnijmy, że naszym celem jest udowodnienie następującego twierdzenia.
Przypomnijmy, że naszym celem jest udowodnienie następującego twierdzenia.
Twierdzenie 1. Jeśli 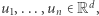 dla każdego
dla każdego 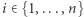 zachodzi
zachodzi 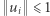 oraz
oraz  to istnieje permutacja
to istnieje permutacja  ciągu
ciągu 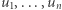 taka, że dla każdego
taka, że dla każdego 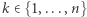 mamy
mamy 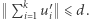
Załóżmy, że 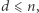 inaczej wniosek jest trywialny. Udowodnimy następujący lemat.
inaczej wniosek jest trywialny. Udowodnimy następujący lemat.
Zobaczmy najpierw, jak z lematu wynika twierdzenie 1. Dla dowolnego 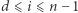 zbiór
zbiór  ma dokładnie jeden element, nazywamy go
ma dokładnie jeden element, nazywamy go 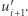 Pozostałych
Pozostałych 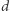 elementów ciągu
elementów ciągu 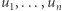 dowolnie przypisujemy na
dowolnie przypisujemy na 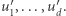 Dla
Dla  nierówność z twierdzenia jest oczywista, załóżmy
nierówność z twierdzenia jest oczywista, załóżmy  Mamy
Mamy
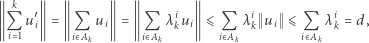 |
gdzie druga i ostatnia równość wynikają wprost z lematu. Wystarczy więc udowodnić lemat.
Pokażemy istnienie zbiorów 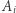 oraz wag
oraz wag  spełniających warunki lematu przez indukcję po
spełniających warunki lematu przez indukcję po 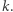 Zacznijmy od bazy indukcji dla
Zacznijmy od bazy indukcji dla 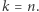 Wówczas ustalamy
Wówczas ustalamy  oraz
oraz 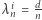 dla każdego
dla każdego 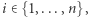 które, jak łatwo sprawdzić, spełniają warunki. Aby wykonać krok indukcyjny z
które, jak łatwo sprawdzić, spełniają warunki. Aby wykonać krok indukcyjny z 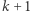 do
do  załóżmy, że mamy zdefiniowany zbiór
załóżmy, że mamy zdefiniowany zbiór 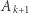 oraz wagi
oraz wagi 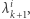 a chcemy zdefiniować zbiór
a chcemy zdefiniować zbiór 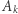 oraz wagi
oraz wagi 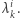 Niech
Niech 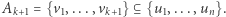
Rozważmy następujący układ równań i nierówności z 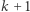 zmiennymi
zmiennymi 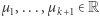 :
: 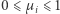 dla dowolnego
dla dowolnego 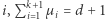 oraz
oraz 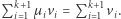 Zbiór rozwiązań
Zbiór rozwiązań 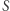 tego układu jest niepusty, gdyż, jak nietrudno sprawdzić, rozwiązaniem jest
tego układu jest niepusty, gdyż, jak nietrudno sprawdzić, rozwiązaniem jest 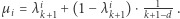 W ogólności dla każdego układu
W ogólności dla każdego układu 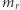 równań i
równań i 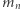 nierówności liniowych w
nierówności liniowych w 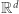 zbiór rozwiązań jest wielościanem, o ile jest ograniczony. Co więcej, okazuje się, że w każdym wierzchołku tego wielościanu dokładnie
zbiór rozwiązań jest wielościanem, o ile jest ograniczony. Co więcej, okazuje się, że w każdym wierzchołku tego wielościanu dokładnie 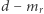 nierówności staje się równościami. Nietrudno w to uwierzyć, bo skoro mamy do czynienia z wierzchołkiem, to liczba równości powinna być równa wymiarowi przestrzeni, a
nierówności staje się równościami. Nietrudno w to uwierzyć, bo skoro mamy do czynienia z wierzchołkiem, to liczba równości powinna być równa wymiarowi przestrzeni, a 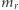 równości mamy już gotowe z równań. Zachęcamy Czytelników do precyzyjnego wykazania tego faktu. Wybierzmy więc dowolny wierzchołek wielościanu
równości mamy już gotowe z równań. Zachęcamy Czytelników do precyzyjnego wykazania tego faktu. Wybierzmy więc dowolny wierzchołek wielościanu 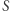 zawierającego rozwiązania naszego układu równań. W układzie mamy
zawierającego rozwiązania naszego układu równań. W układzie mamy 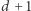 równości (równość
równości (równość 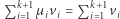 jest w istocie równością na każdej z
jest w istocie równością na każdej z 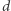 współrzędnych) oraz
współrzędnych) oraz 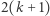 nierówności. A zatem w wierzchołku
nierówności. A zatem w wierzchołku 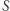 spełnionych jest
spełnionych jest 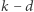 dodatkowych równości spośród nierówności
dodatkowych równości spośród nierówności 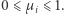 Chcemy wykazać, że istnieje
Chcemy wykazać, że istnieje 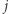 takie, że
takie, że 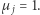 Jedyny przypadek, w którym nie jest to natychmiastowe, to gdy każda ze wspomnianych
Jedyny przypadek, w którym nie jest to natychmiastowe, to gdy każda ze wspomnianych 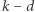 równości jest postaci
równości jest postaci 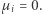 Wiemy jednak, że wówczas suma pozostałych
Wiemy jednak, że wówczas suma pozostałych 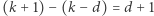 zmiennych
zmiennych  jest równa
jest równa 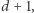 więc każda z nich musi być równa jeden. A więc tak czy inaczej istnieje
więc każda z nich musi być równa jeden. A więc tak czy inaczej istnieje  takie, że
takie, że 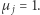 Definiujemy więc
Definiujemy więc 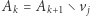 oraz
oraz  Nietrudno sprawdzić, że istotnie wszystkie warunki są spełnione, co kończy dowód lematu.
Nietrudno sprawdzić, że istotnie wszystkie warunki są spełnione, co kończy dowód lematu.
Czy oprócz ładnego dowodu i ciekawej historii oszacowanie na stałą w lemacie Steinitza przydaje się do czegoś? Tak, zdecydowanie, przykładem może być ta praca arxiv.org/abs/1707.00481 opublikowana na konferencji SODA w 2018 roku, jednej z najlepszych światowych konferencji informatycznych. Gwoli ścisłości należy przyznać, że użyta jest tam konkretna norma: norma maksimum oznaczana 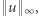 przypomnijmy, że przypisuje ona wektorowi
przypomnijmy, że przypisuje ona wektorowi 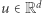 maksimum z wartości bezwzględnych jego współrzędnych. A więc do tego konkretnego zastosowania wystarczyłby już oryginalny wynik Steinitza z 1914 roku. Faktycznie, z tego, że dla
maksimum z wartości bezwzględnych jego współrzędnych. A więc do tego konkretnego zastosowania wystarczyłby już oryginalny wynik Steinitza z 1914 roku. Faktycznie, z tego, że dla 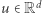 zachodzi
zachodzi  (
(  oznacza długość euklidesową wektora
oznacza długość euklidesową wektora  ), oraz tego, że
), oraz tego, że 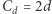 wystarcza dla normy euklidesowej, wynika, że
wystarcza dla normy euklidesowej, wynika, że 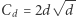 wystarcza dla normy maksimum. Ja przedstawię pokrótce inne zastosowanie, które wydaje mi się również interesujące, a może być też bardzo użyteczne.
wystarcza dla normy maksimum. Ja przedstawię pokrótce inne zastosowanie, które wydaje mi się również interesujące, a może być też bardzo użyteczne.
Tunelem pomiędzy punktem 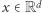 a
a 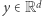 o promieniu
o promieniu 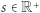 nazwijmy zbiór, który zawiera odcinek pomiędzy
nazwijmy zbiór, który zawiera odcinek pomiędzy 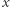 a
a  oraz punkty, które są oddalone od tego odcinka o co najwyżej
oraz punkty, które są oddalone od tego odcinka o co najwyżej 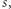 gdzie odległość mierzymy normą maksimum. Precyzyjnie rzecz biorąc, taki tunel to zbiór
gdzie odległość mierzymy normą maksimum. Precyzyjnie rzecz biorąc, taki tunel to zbiór
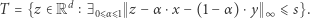 |
Po pierwsze zauważmy, że z twierdzenia 1 prosto wynika następujący wniosek.
Wniosek 1. Jeśli 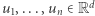 oraz dla każdego
oraz dla każdego 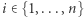 zachodzi
zachodzi 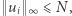 to istnieje permutacja
to istnieje permutacja 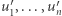 ciągu
ciągu 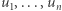 taka, że podróż z punktu
taka, że podróż z punktu 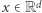 do punktu
do punktu 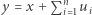 ciągiem
ciągiem 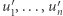 odbywa się wewnątrz tunelu pomiędzy
odbywa się wewnątrz tunelu pomiędzy  a
a 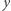 o promieniu
o promieniu 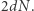
Zachęcamy Czytelnika do samodzielnego wykazania wniosku, dowód jest nietrudny. Jesteśmy już gotowi do sformułowania twierdzenia.
Twierdzenie 2. Rozważmy układ  równań liniowych
równań liniowych 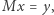 gdzie
gdzie 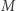 jest macierzą o współczynnikach całkowitych
jest macierzą o współczynnikach całkowitych  a
a  wektorem z
wektorem z 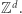 Niech
Niech 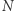 będzie maksimum z wartości bezwzględnych liczb występujących w macierzy
będzie maksimum z wartości bezwzględnych liczb występujących w macierzy 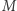 i wektorze
i wektorze 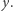 Wówczas jeśli istnieje pewne rozwiązanie tego układu w liczbach naturalnych, to istnieje również rozwiązanie
Wówczas jeśli istnieje pewne rozwiązanie tego układu w liczbach naturalnych, to istnieje również rozwiązanie 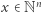 takie, że
takie, że 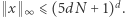
Zauważmy, że ograniczenie na normę rozwiązania nie zależy od liczby równań 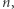 a jedynie od liczby zmiennych
a jedynie od liczby zmiennych 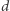 i wielkości liczb
i wielkości liczb 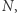 i to jest właśnie główna siła twierdzenia 2. Aby udowodnić twierdzenie 2, oznaczmy kolumny macierzy
i to jest właśnie główna siła twierdzenia 2. Aby udowodnić twierdzenie 2, oznaczmy kolumny macierzy 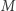 jako wektory
jako wektory 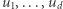 oraz
oraz 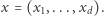 Wówczas równanie
Wówczas równanie 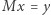 przyjmuje postać
przyjmuje postać 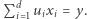 Rozważmy pewne rozwiązanie tego układu, które istnieje zgodnie z założeniem twierdzenia 2. Zawiera ono
Rozważmy pewne rozwiązanie tego układu, które istnieje zgodnie z założeniem twierdzenia 2. Zawiera ono 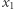 wektorów
wektorów 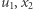 wektorów
wektorów 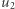 itd., aż w końcu
itd., aż w końcu 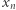 wektorów
wektorów 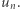 Zgodnie z wnioskiem istnieje taka permutacja
Zgodnie z wnioskiem istnieje taka permutacja 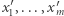 tych
tych  wektorów, że cała podróż z punktu 0 do punktu
wektorów, że cała podróż z punktu 0 do punktu  ciągiem
ciągiem 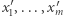 odbywa się wewnątrz tunelu z 0 do
odbywa się wewnątrz tunelu z 0 do 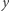 o promieniu
o promieniu 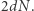 Taki tunel zawiera się cały w
Taki tunel zawiera się cały w  -wymiarowej kostce o boku
-wymiarowej kostce o boku 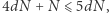 na potrzeby dowodu twierdzenia 2 wystarczy nam takie zgrubne oszacowanie. Zauważmy, że jeśli w trakcie naszej podróży odwiedzimy dwa razy ten sam punkt, to możemy tę podróż skrócić, pomijając pętlę wychodzącą i wracającą do tego samego punktu, nie zmieni to oczywiście celu podróży. Postępując w ten sposób, możemy skrócić podróż ciągiem
na potrzeby dowodu twierdzenia 2 wystarczy nam takie zgrubne oszacowanie. Zauważmy, że jeśli w trakcie naszej podróży odwiedzimy dwa razy ten sam punkt, to możemy tę podróż skrócić, pomijając pętlę wychodzącą i wracającą do tego samego punktu, nie zmieni to oczywiście celu podróży. Postępując w ten sposób, możemy skrócić podróż ciągiem 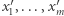 do takiej podróży, która każdy punkt w kostce o boku
do takiej podróży, która każdy punkt w kostce o boku 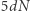 odwiedza co najwyżej jeden raz. Punktów o współczynnikach całkowitych w kostce jest nie więcej niż
odwiedza co najwyżej jeden raz. Punktów o współczynnikach całkowitych w kostce jest nie więcej niż 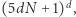 a więc nasza podróż będzie miała co najwyżej tyle kroków. Nietrudno zauważyć, że dowolna taka podróż natychmiast daje rozwiązanie równania
a więc nasza podróż będzie miała co najwyżej tyle kroków. Nietrudno zauważyć, że dowolna taka podróż natychmiast daje rozwiązanie równania 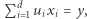 gdzie
gdzie 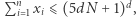 co kończy dowód twierdzenia 2.
co kończy dowód twierdzenia 2.
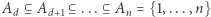
![λi ∈[0,1] k](/math/temat/matematyka/algebra/2020/06/21/podroze-w-R-d/3x-824d19e84db070d2ad3cfcbad6463fc29d114e6c-im-33,33,33-FF,FF,FF.gif)