Co to jest?
Grupa
Ustalmy zbiór 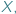 np.
np. 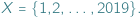 Niech
Niech  oznacza zbiór funkcji odwracalnych z
oznacza zbiór funkcji odwracalnych z 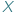 w
w 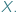 Funkcje z
Funkcje z  można składać i odwracać, nie wychodząc poza
można składać i odwracać, nie wychodząc poza 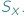 W zbiorze
W zbiorze  istnieje też funkcja identycznościowa. Tytułowe grupy są abstrakcyjnym sposobem wyrażenia powyższych własności zbioru
istnieje też funkcja identycznościowa. Tytułowe grupy są abstrakcyjnym sposobem wyrażenia powyższych własności zbioru 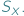
Grupa to zbiór 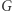 wraz z działaniem mnożenia, czyli funkcją
wraz z działaniem mnożenia, czyli funkcją 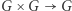 oznaczaną
oznaczaną 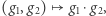 elementem neutralnym
elementem neutralnym 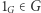 oraz działaniem odwracania
oraz działaniem odwracania 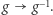 Działania mnożenia i odwracania oraz element neutralny są częścią definicji grupy i wymagamy, by spełniały one wszystkie naturalne własności z przykładu
Działania mnożenia i odwracania oraz element neutralny są częścią definicji grupy i wymagamy, by spełniały one wszystkie naturalne własności z przykładu  (patrz margines).
(patrz margines).
Przykładowo, zbiór 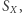 w którym "mnożenie" to składanie funkcji, odwracanie to odwracanie funkcji, a jedynka to funkcja identycznościowa, jest grupą. Zbiór
w którym "mnożenie" to składanie funkcji, odwracanie to odwracanie funkcji, a jedynka to funkcja identycznościowa, jest grupą. Zbiór 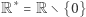 ze zwykłym mnożeniem i odwracaniem także jest grupą, podobnie zbiór
ze zwykłym mnożeniem i odwracaniem także jest grupą, podobnie zbiór 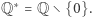 Zbiór
Zbiór 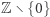 z mnożeniem i dzieleniem nie jest grupą, bo odwrotność liczby całkowitej zwykle nie jest liczbą całkowitą. Jeśli
z mnożeniem i dzieleniem nie jest grupą, bo odwrotność liczby całkowitej zwykle nie jest liczbą całkowitą. Jeśli 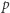 jest liczbą pierwszą, to zbiór
jest liczbą pierwszą, to zbiór 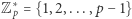 z mnożeniem modulo
z mnożeniem modulo 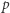 jest grupą, bo z algorytmu Euklidesa wynika, że dla każdej liczby
jest grupą, bo z algorytmu Euklidesa wynika, że dla każdej liczby 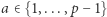 istnieją liczby całkowite
istnieją liczby całkowite 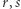 takie, że
takie, że 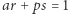 ; reszta z dzielenia
; reszta z dzielenia  przez
przez  jest odwrotnością
jest odwrotnością 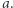 Grupą jest także zbiór
Grupą jest także zbiór 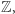 w którym "mnożenie" to dodawanie, zaś "odwrotność" to
w którym "mnożenie" to dodawanie, zaś "odwrotność" to 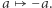 Podobnie, zbiór
Podobnie, zbiór 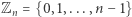 z dodawaniem modulo
z dodawaniem modulo  jest grupą. Notabene, twierdzenie o generatorze z teorii liczb mówi, że grupa
jest grupą. Notabene, twierdzenie o generatorze z teorii liczb mówi, że grupa 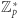 jest izomorficzna z grupą
jest izomorficzna z grupą  Wreszcie, jeszcze bardziej egzotyczne grupy pojawiają się w kryptografii (patrz Krzywe eliptyczne w kryptografii, Delta 08/2018.
Wreszcie, jeszcze bardziej egzotyczne grupy pojawiają się w kryptografii (patrz Krzywe eliptyczne w kryptografii, Delta 08/2018.
Podgrupa grupy  to podzbiór
to podzbiór 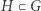 taki, że działania wykonywane na elementach z
taki, że działania wykonywane na elementach z 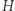 dają w wyniku element z
dają w wyniku element z 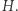 Formalnie mówiąc, dla każdych
Formalnie mówiąc, dla każdych 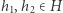 zachodzi
zachodzi 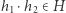 oraz
oraz  Jedno z podstawowych twierdzeń teorii grup mówi, że każda grupa
Jedno z podstawowych twierdzeń teorii grup mówi, że każda grupa 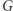 jest podgrupą
jest podgrupą 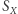 dla odpowiednio dużego zbioru
dla odpowiednio dużego zbioru 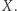 Definicja grupy nie odchodzi więc zbyt daleko od przykładu
Definicja grupy nie odchodzi więc zbyt daleko od przykładu 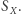 Jeśli
Jeśli  jest podgrupą
jest podgrupą 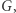 to zbiór
to zbiór 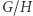 powstaje z
powstaje z 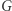 przez utożsamienie elementów
przez utożsamienie elementów 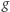 i
i  dla każdych
dla każdych 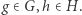 Prawdziwy jest następujący elegancki wzór:
Prawdziwy jest następujący elegancki wzór:  a zatem liczność podgrupy jest zawsze dzielnikiem liczności grupy.
a zatem liczność podgrupy jest zawsze dzielnikiem liczności grupy.
Specjalną klasą podgrup są podgrupy normalne. Podgrupa 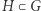 jest normalna, jeśli zachodzi
jest normalna, jeśli zachodzi 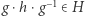 dla każdych
dla każdych 
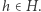 Ten dziwaczny warunek pozwala wprowadzić na zbiorze
Ten dziwaczny warunek pozwala wprowadzić na zbiorze 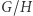 strukturę grupy. W każdej grupie
strukturę grupy. W każdej grupie  podgrupami normalnymi są
podgrupami normalnymi są 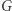 i
i 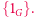 Grupy, które nie mają innych podgrup normalnych, nazywane są prostymi, np. grupa
Grupy, które nie mają innych podgrup normalnych, nazywane są prostymi, np. grupa 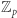 jest prosta (gdyż rozmiar podgrupy musi być dzielnikiem rozmiaru grupy), a grupa
jest prosta (gdyż rozmiar podgrupy musi być dzielnikiem rozmiaru grupy), a grupa  nie jest. W XX wieku sklasyfikowano wszystkie grupy proste. Tworzą one
nie jest. W XX wieku sklasyfikowano wszystkie grupy proste. Tworzą one 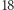 "rodzin" i
"rodzin" i 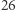 "nieoczekiwanych" grup sporadycznych. Te ostatnie święcą dziś triumfy w matematycznych modelach teorii strun, w ramach tzw. moonshine theory.
"nieoczekiwanych" grup sporadycznych. Te ostatnie święcą dziś triumfy w matematycznych modelach teorii strun, w ramach tzw. moonshine theory.
Dlaczego jednak grupy pojawiają się w innych gałęziach matematyki i fizyki? Okazuje się, że grupy dobrze obrazują (odwracalne) działania na obiektach. Grupa 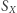 w naturalny sposób działa na zbiorze
w naturalny sposób działa na zbiorze 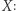 jeśli weźmiemy element
jeśli weźmiemy element  oraz
oraz 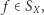 to możemy otrzymać nowy element
to możemy otrzymać nowy element 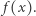
Jak poprzednio, tworzymy z tego abstrakcyjną definicję: działanie grupy 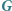 na zbiorze
na zbiorze 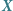 jest to odwzorowanie
jest to odwzorowanie 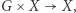 zapisywane jako
zapisywane jako  takie że
takie że  oraz
oraz 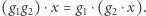
To właśnie działania grup czynią grupy tak interesującymi i wszechobecnymi obiektami w matematyce. Żeby zobaczyć to lepiej, rozważmy przypadek, gdy  ma dodatkową strukturę, np. gdy niektóre pary elementów
ma dodatkową strukturę, np. gdy niektóre pary elementów  połączymy, otrzymując graf
połączymy, otrzymując graf  W tej sytuacji możemy zadać następujące pytania:
W tej sytuacji możemy zadać następujące pytania:
- Które elementy
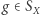 spełniają warunek
spełniają warunek  Zbiór takich elementów nazywamy stabilizatorem
Zbiór takich elementów nazywamy stabilizatorem 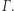 Stabilizator jest naturalnie podgrupą
Stabilizator jest naturalnie podgrupą 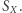 Oznaczamy go
Oznaczamy go 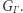
- Które grafy można otrzymać z
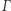 przez permutowanie wierzchołków? Zbiór takich grafów nazywamy orbitą
przez permutowanie wierzchołków? Zbiór takich grafów nazywamy orbitą  przy działaniu
przy działaniu  i oznaczamy
i oznaczamy 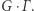
- Jeśli popatrzymy na zbiór
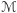 wszystkich możliwych grafów o wierzchołkach
wszystkich możliwych grafów o wierzchołkach 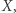 to ile jest orbit? Zbiór orbit oznaczamy przez
to ile jest orbit? Zbiór orbit oznaczamy przez 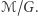
Warto sprawdzić, że jedyne grafy ze stabilizatorem równym 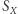 to graf pełny oraz graf pusty. Zachodzi też równanie
to graf pełny oraz graf pusty. Zachodzi też równanie 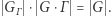 Wynika stąd, że im większa orbita, tym mniejszy stabilizator, a ponadto: liczby
Wynika stąd, że im większa orbita, tym mniejszy stabilizator, a ponadto: liczby 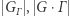 są dzielnikami
są dzielnikami 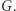 Znacznie bardziej skomplikowane jest sprawdzenie, ile jest orbit, czyli ile elementów ma zbiór
Znacznie bardziej skomplikowane jest sprawdzenie, ile jest orbit, czyli ile elementów ma zbiór 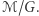 Tym niemniej czasem można powiedzieć coś o orbitach, mając bardzo niewiele danych:
Tym niemniej czasem można powiedzieć coś o orbitach, mając bardzo niewiele danych:
Lemat. Jeśli 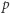 jest pierwsza, grupa
jest pierwsza, grupa  ma
ma 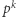 elementów i działa na zbiorze
elementów i działa na zbiorze  który ma niepodzielną przez
który ma niepodzielną przez 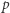 liczbę elementów, to istnieje element stały, tzn.
liczbę elementów, to istnieje element stały, tzn. 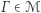 taki, że
taki, że 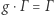 dla wszystkich
dla wszystkich 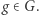
Dowód. Faktycznie, 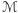 jest sumą orbit, a rozmiar każdej orbity dzieli
jest sumą orbit, a rozmiar każdej orbity dzieli 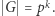 Jeśli żadna orbita nie jest jednoelementowa, to rozmiar każdej jest podzielny przez
Jeśli żadna orbita nie jest jednoelementowa, to rozmiar każdej jest podzielny przez 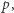 zatem i
zatem i 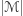 jest podzielna przez
jest podzielna przez 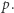 Sprzeczność. A więc istnieje
Sprzeczność. A więc istnieje  takie, że
takie, że 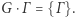
Zamiast grafów można podobnie analizować inne obiekty. Jeśli będziemy patrzeć na przestrzenie liniowe, to otrzymamy teorię reprezentacji, jeśli na ciała (patrz poniżej), to teorię Galois, itd. Wreszcie, aby lepiej zrozumieć same grupy, warto badać działania grup na grupach.
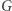 i
i  to bijekcja
to bijekcja 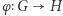 taka, że zachodzi
taka, że zachodzi 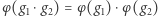 dla wszystkich
dla wszystkich 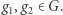 Wspomniany izomorfizm np. dla
Wspomniany izomorfizm np. dla  można łatwo wskazać: jest to funkcja
można łatwo wskazać: jest to funkcja 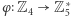 zadana wzorem
zadana wzorem  Konkretniej mówiąc:
Konkretniej mówiąc: 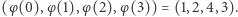 Liczba
Liczba 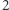 zwana jest generatorem grupy
zwana jest generatorem grupy 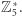
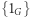 jest podgrupą, i zauważyć analogię pomiędzy grupami prostymi a liczbami pierwszymi.
jest podgrupą, i zauważyć analogię pomiędzy grupami prostymi a liczbami pierwszymi.