Ile jest podprzestrzeni?
Jaka jest liczba różnych  -elementowych podzbiorów zbioru
-elementowych podzbiorów zbioru 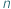 -elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez
-elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez  (symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...
(symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...
Słowo zbiór zamienimy na przestrzeń liniowa nad ciałem skończonym, podzbiór na podprzestrzeń. Zamiast mocy zbioru (w tym przypadku liczby elementów) będziemy rozważać wymiar przestrzeni. Możemy teraz zadać analogiczne pytanie w świecie przestrzeni liniowych.
Problem. Jaka jest liczba różnych  -wymiarowych podprzestrzeni liniowych przestrzeni
-wymiarowych podprzestrzeni liniowych przestrzeni 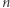 -wymiarowej nad
-wymiarowej nad 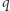 -elementowym ciałem?
-elementowym ciałem?
Zanim poznamy odpowiedź na to pytanie, przybliżymy pojęcia, których ono dotyczy.
Rozważmy zbiór reszt z dzielenia przez liczbę pierwszą 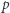 z dodawaniem i mnożeniem modulo
z dodawaniem i mnożeniem modulo  Dla przykładu, przy
Dla przykładu, przy 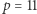 mamy
mamy 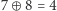 oraz
oraz 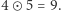 Działania te mają, przedstawione na marginesie, naturalne własności, dzięki czemu zaprezentowaną strukturę możemy nazywać ciałem (które, rzecz jasna, jest skończone). Przedstawiony sposób nie jest jedynym, w jaki można otrzymać skończone ciało - na potrzeby naszych rozważań istotny jest jednak tylko fakt, że takie struktury istnieją.
Działania te mają, przedstawione na marginesie, naturalne własności, dzięki czemu zaprezentowaną strukturę możemy nazywać ciałem (które, rzecz jasna, jest skończone). Przedstawiony sposób nie jest jedynym, w jaki można otrzymać skończone ciało - na potrzeby naszych rozważań istotny jest jednak tylko fakt, że takie struktury istnieją.
Niech 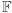 będzie ciałem skończonym. Rozważmy zbiór wszystkich
będzie ciałem skończonym. Rozważmy zbiór wszystkich 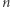 -elementowych ciągów liczb z
-elementowych ciągów liczb z 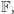 czyli
czyli 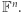 Takie ciągi można w naturalny sposób dodawać i mnożyć przez liczby z
Takie ciągi można w naturalny sposób dodawać i mnożyć przez liczby z  na przykład (wracając do opisanego wcześniej ciała reszt z dzielenia przez 11 oraz biorąc
na przykład (wracając do opisanego wcześniej ciała reszt z dzielenia przez 11 oraz biorąc 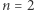 ) mamy
) mamy 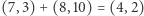 oraz
oraz 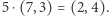 Działania te są "porządne", to znaczy spełniają prawa łączności, przemienności i rozdzielności. Sprawia to, że
Działania te są "porządne", to znaczy spełniają prawa łączności, przemienności i rozdzielności. Sprawia to, że 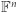 możemy traktować jako przestrzeń liniową nad ciałem
możemy traktować jako przestrzeń liniową nad ciałem 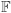 ; jej elementy będziemy nazywać wektorami.
; jej elementy będziemy nazywać wektorami.
Niektóre podzbiory  są bardzo szczególne i nie można z nich "uciec", dodając dowolne dwa ich elementy oraz mnożąc je przez liczbę z
są bardzo szczególne i nie można z nich "uciec", dodając dowolne dwa ich elementy oraz mnożąc je przez liczbę z 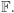 Takie zbiory nazywamy podprzestrzeniami wyjściowej przestrzeni - nazwa jest bardzo naturalna, gdyż podprzestrzenie same w sobie mogą być traktowane jako przestrzenie liniowe nad rozważanym ciałem. Przykładem jest zbiór ciągów stałych. Nieco ogólniej, wystarczy wziąć dowolny wektor
Takie zbiory nazywamy podprzestrzeniami wyjściowej przestrzeni - nazwa jest bardzo naturalna, gdyż podprzestrzenie same w sobie mogą być traktowane jako przestrzenie liniowe nad rozważanym ciałem. Przykładem jest zbiór ciągów stałych. Nieco ogólniej, wystarczy wziąć dowolny wektor  z naszej przestrzeni i rozpatrzeć zbiór jego wielokrotności, tzn. wektorów postaci
z naszej przestrzeni i rozpatrzeć zbiór jego wielokrotności, tzn. wektorów postaci 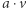 dla
dla  Podprzestrzenie tej postaci nazywamy jednowymiarowymi. Jak możemy zwiększyć ich wymiar? Wystarczy znaleźć wektor
Podprzestrzenie tej postaci nazywamy jednowymiarowymi. Jak możemy zwiększyć ich wymiar? Wystarczy znaleźć wektor 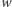 spoza tej podprzestrzeni i rozważyć zbiór wektorów postaci
spoza tej podprzestrzeni i rozważyć zbiór wektorów postaci 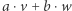 (są to kombinacje liniowe wektorów
(są to kombinacje liniowe wektorów  i
i 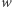 ) - to też będzie podprzestrzeń, już dwuwymiarowa. Ogólnie, podprzestrzeń
) - to też będzie podprzestrzeń, już dwuwymiarowa. Ogólnie, podprzestrzeń 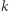 -wymiarowa składa się z kombinacji liniowych układu
-wymiarowa składa się z kombinacji liniowych układu  wektorów o tej własności, że żaden z nich nie jest kombinacją liniową pozostałych (o takim układzie mówimy, że jest liniowo niezależny).
wektorów o tej własności, że żaden z nich nie jest kombinacją liniową pozostałych (o takim układzie mówimy, że jest liniowo niezależny).

Możemy już przejść do wyjściowego pytania. Przestrzeń 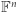 składa się z
składa się z 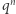 wektorów (gdzie
wektorów (gdzie 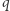 to liczba elementów
to liczba elementów  ). Chcemy wyznaczyć liczbę jej różnych
). Chcemy wyznaczyć liczbę jej różnych 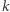 -wymiarowych podprzestrzeni liniowych. Będziemy ją oznaczać przez
-wymiarowych podprzestrzeni liniowych. Będziemy ją oznaczać przez 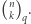
Do opisania podprzestrzeni  -wymiarowej wystarczy wskazać
-wymiarowej wystarczy wskazać 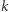 liniowo niezależnych wektorów
liniowo niezależnych wektorów 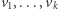 z tej przestrzeni. Ponieważ poruszamy się po przestrzeni nad ciałem skończonym, to wyznaczenie liczby takich
z tej przestrzeni. Ponieważ poruszamy się po przestrzeni nad ciałem skończonym, to wyznaczenie liczby takich 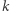 -tek sprowadza się do prostego przeliczenia. Wybierzmy najpierw wektor
-tek sprowadza się do prostego przeliczenia. Wybierzmy najpierw wektor 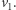 Jedyne, o co musimy się zatroszczyć, to żeby był on różny od wektora zerowego. Ze wszystkich
Jedyne, o co musimy się zatroszczyć, to żeby był on różny od wektora zerowego. Ze wszystkich 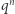 wektorów, które są dostępne, musimy wykluczyć tylko ten jeden. Wektor
wektorów, które są dostępne, musimy wykluczyć tylko ten jeden. Wektor 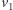 możemy zatem wybrać na
możemy zatem wybrać na 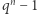 sposobów.
sposobów.
Na wektor  mamy już odrobinę mniej kandydatów. Nie może on należeć do podprzestrzeni rozpinanej przez wektor
mamy już odrobinę mniej kandydatów. Nie może on należeć do podprzestrzeni rozpinanej przez wektor 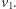 Elementów tej podprzestrzeni jest tyle, na ile sposobów możemy pomnożyć ten wektor przez element ciała
Elementów tej podprzestrzeni jest tyle, na ile sposobów możemy pomnożyć ten wektor przez element ciała 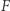 (tych elementów jest
(tych elementów jest 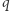 ). Wektor
). Wektor 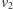 wybieramy zatem na
wybieramy zatem na 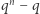 sposobów.
sposobów.
Wektor  nie może należeć do podprzestrzeni rozpiętej przez oba wcześniej wybrane. Wykluczamy więc dokładnie
nie może należeć do podprzestrzeni rozpiętej przez oba wcześniej wybrane. Wykluczamy więc dokładnie 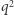 wektorów.
wektorów.
Jeżeli wybraliśmy już 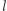 wektorów, to kolejny nie może być kombinacją liniową poprzednich, w związku z czym mamy już tylko
wektorów, to kolejny nie może być kombinacją liniową poprzednich, w związku z czym mamy już tylko 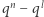 możliwości. Różnych
możliwości. Różnych 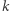 -tek wektorów niezależnych mamy więc
-tek wektorów niezależnych mamy więc

Oczywiście, niektóre układy wektorów generują te same podprzestrzenie, nas interesują te generujące różne. Każdą podprzestrzeń wymiaru 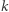 możemy uzyskać na tyle sposobów, ile różnych
możemy uzyskać na tyle sposobów, ile różnych 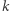 -tek wektorów niezależnych w niej znajdziemy. Wiemy dokładnie, ile jest takich
-tek wektorów niezależnych w niej znajdziemy. Wiemy dokładnie, ile jest takich 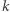 -tek (przed chwilą właśnie to policzyliśmy!):
-tek (przed chwilą właśnie to policzyliśmy!):

Zatem ostatecznie szukana przez nas liczba wyraża się następująco:

Wzór ten nie jest nowy, a dobór oznaczenia nie jest przypadkowy. Formuła ta nazywana jest współczynnikiem dwumianowym Gaussa, a pierwszy raz została użyta przez tego słynnego matematyka do znalezienia wzoru na tak zwane sumy Gaussa. Ale czy ma ona, oprócz nazwy, jakiś bliższy związek ze współczynnikiem dwumianowym Newtona? Przyjrzyjmy się bliżej. Przypomnijmy, że zachodzi algebraiczna równość 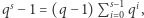 w związku z czym powyższy ułamek można "skrócić" przez
w związku z czym powyższy ułamek można "skrócić" przez 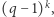 otrzymując
otrzymując
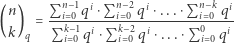 |
(*) |
Jeżeli zatem potraktujemy 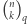 jak funkcję zmiennej rzeczywistej
jak funkcję zmiennej rzeczywistej 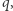 dostaniemy
dostaniemy 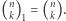 Widzimy więc wyraźnie, że coś jest na rzeczy. Tylko, że po analitycznym podejściu do sprawy trudno nam powiedzieć coś oprócz tego, iż zależność (której zresztą się spodziewaliśmy) istnieje. A gdybyśmy chcieli poczuć jej istotę? Zrozumieć charakter? W tym celu musimy się udać po pomoc do Donalda Knutha, który podszedł do sprawy z zupełnie innej strony.
Widzimy więc wyraźnie, że coś jest na rzeczy. Tylko, że po analitycznym podejściu do sprawy trudno nam powiedzieć coś oprócz tego, iż zależność (której zresztą się spodziewaliśmy) istnieje. A gdybyśmy chcieli poczuć jej istotę? Zrozumieć charakter? W tym celu musimy się udać po pomoc do Donalda Knutha, który podszedł do sprawy z zupełnie innej strony.
Spróbujmy jeszcze raz zliczyć podprzestrzenie wymiaru 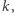 tym razem innym sposobem. Po pierwsze, umieśćmy wektory
tym razem innym sposobem. Po pierwsze, umieśćmy wektory  w macierzy, jako jej wiersze. Taką macierz możemy, poprzez elementarne operacje na wierszach, sprowadzić do tak zwanej zredukowanej postaci schodkowej
w macierzy, jako jej wiersze. Taką macierz możemy, poprzez elementarne operacje na wierszach, sprowadzić do tak zwanej zredukowanej postaci schodkowej

Można udowodnić, że jeżeli wiersze dwóch takich macierzy generują tę samą przestrzeń, to macierze te są równe. Zliczenie wszystkich interesujących nas podprzestrzeni sprowadza się więc do policzenia, ile jest różnych zredukowanych macierzy schodkowych. Żeby je policzyć, spróbujmy usunąć z takiej macierzy wszystko, co "zbędne". Z pewnością zbędne są wszystkie zera, na lewo od jedynek wiodących. Możemy je więc bezkarnie usunąć. Kolumny zawierające wiodące jedynki również nie będą miały dla nas znaczenia, więc je też usuńmy.
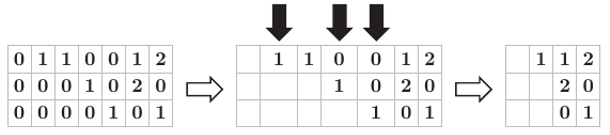
Otrzymaliśmy macierz zawierającą puste pola oraz pewne liczby. Tak naprawdę nie interesuje nas, jakie to są liczby, więc możemy każdą z nich zastąpić gwiazdką.

Czyli mamy diagram o wymiarach 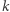 na
na 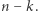 Oznaczmy pojedynczy diagram przez
Oznaczmy pojedynczy diagram przez 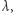 a liczbę gwiazdek w nim przez
a liczbę gwiazdek w nim przez 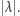 Zauważmy, że z diagramu
Zauważmy, że z diagramu 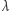 możemy "odzyskać" postać macierzy, z której powstał. Kolumny z jedynkami wiodącymi wstawiamy w sposób jednoznaczny, podobnie jak zera po ich lewej stronie. Natomiast gwiazdki możemy zastąpić elementami ciała
możemy "odzyskać" postać macierzy, z której powstał. Kolumny z jedynkami wiodącymi wstawiamy w sposób jednoznaczny, podobnie jak zera po ich lewej stronie. Natomiast gwiazdki możemy zastąpić elementami ciała  na wszystkie możliwe sposoby, których jest dokładnie
na wszystkie możliwe sposoby, których jest dokładnie 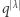
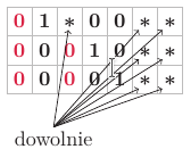

I tak oto dochodzimy do wniosku, że różnych zredukowanych macierzy schodkowych, a więc również podprzestrzeni 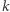 -wymiarowych przestrzeni
-wymiarowych przestrzeni 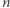 -wymiarowej jest:
-wymiarowej jest:
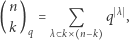 |
(**) |
gdzie zapis 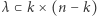 oznacza, że diagram
oznacza, że diagram 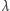 "mieści" się w macierzy o
"mieści" się w macierzy o 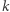 wierszach i
wierszach i  kolumnach. Z powyższej formuły widać ponadto, że
kolumnach. Z powyższej formuły widać ponadto, że  wyraża się zawsze jako wielomian stopnia
wyraża się zawsze jako wielomian stopnia 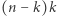 zmiennej
zmiennej 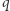 o całkowitych dodatnich współczynnikach. To nie było od razu widoczne z formuły (*), gdyż na pozór nie wydaje się, aby występujący tam ułamek mógł zostać skrócony. Warto również podkreślić, że równość pomiędzy prawymi stronami równań (*) i (**) zachodzi dla dowolnej liczby rzeczywistej
o całkowitych dodatnich współczynnikach. To nie było od razu widoczne z formuły (*), gdyż na pozór nie wydaje się, aby występujący tam ułamek mógł zostać skrócony. Warto również podkreślić, że równość pomiędzy prawymi stronami równań (*) i (**) zachodzi dla dowolnej liczby rzeczywistej 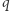 ; na mocy naszych rozważań jest bowiem prawdziwa dla dowolnego
; na mocy naszych rozważań jest bowiem prawdziwa dla dowolnego 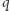 będącego licznością pewnego ciała skończonego (w szczególności dla liczb pierwszych), a jeśli funkcje wymierne (tzn. ilorazy wielomianów) przyjmują te same wartości dla nieskończenie wielu argumentów, to są równe wszędzie tam, gdzie są określone.
będącego licznością pewnego ciała skończonego (w szczególności dla liczb pierwszych), a jeśli funkcje wymierne (tzn. ilorazy wielomianów) przyjmują te same wartości dla nieskończenie wielu argumentów, to są równe wszędzie tam, gdzie są określone.
Pozostało nam jeszcze policzyć, ile jest różnych diagramów o 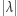 gwiazdkach. Jeżeli przyjrzymy się dokładnie pojedynczemu diagramowi i obrócimy go o
gwiazdkach. Jeżeli przyjrzymy się dokładnie pojedynczemu diagramowi i obrócimy go o  to zobaczymy, że w istocie jest on tym samym, co tak zwany diagram Ferrersa (znany matematykom od dawna i dokładnie zbadany).
to zobaczymy, że w istocie jest on tym samym, co tak zwany diagram Ferrersa (znany matematykom od dawna i dokładnie zbadany).
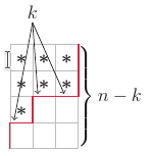
Łatwo policzyć, ile jest takich diagramów. Możemy każdy z nich utożsamić z linią łamaną stanowiącą jego prawostronny obrys (na rysunku diagram Ferrersa dla 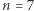 i
i 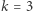 ). Żeby otrzymać taką linię, złożoną z
). Żeby otrzymać taką linię, złożoną z  kresek, musimy wybrać dokładnie
kresek, musimy wybrać dokładnie  miejsc, na których postawimy kreski poziome, a możemy to zrobić na
miejsc, na których postawimy kreski poziome, a możemy to zrobić na 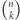 sposobów. Dzięki temu, że policzyliśmy, ile jest różnych diagramów o mocy
sposobów. Dzięki temu, że policzyliśmy, ile jest różnych diagramów o mocy  możemy ponownie stwierdzić słuszność interesującej nas zależności; wystarczy zauważyć, że dla
możemy ponownie stwierdzić słuszność interesującej nas zależności; wystarczy zauważyć, że dla 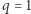 prawa strona (**) jest liczbą wszystkich możliwych diagramów Ferrersa, czyli wynosi
prawa strona (**) jest liczbą wszystkich możliwych diagramów Ferrersa, czyli wynosi 
 często podaje się jako definicję symbolu Newtona, a dopiero później przedstawia jej interpretację kombinatoryczną.
często podaje się jako definicję symbolu Newtona, a dopiero później przedstawia jej interpretację kombinatoryczną.