Jeszcze o algebrze obliczeń kwantowych, czyli artykuł dla Koneserów Macierzy
W poniższym artykule postaramy się przybliżyć Czytelnikowi niektóre podstawowe pojęcia algebry wieloliniowej nad liczbami zespolonymi, która jest podstawą rozważań w kwantowej teorii obliczeń. Bez zbędnej zwłoki przystąpimy od razu do konkretów.
Stany i bramki kwantowe
Stanem komputera kwantowego obsługującego 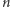 tak zwanych kubitów jest jakiś wektor długości
tak zwanych kubitów jest jakiś wektor długości 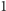 z
z 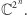 Wykorzystując bardzo sugestywną notację Paula Diraca stan
Wykorzystując bardzo sugestywną notację Paula Diraca stan  w takim komputerze może być zapisany w postaci
w takim komputerze może być zapisany w postaci

Intuicyjnie, możemy sobie więc wyobrażać, że pamięć komputera jest niedeterministyczna i znajduje się w stanie 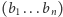 z prawdopodobieństwem
z prawdopodobieństwem 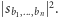 Warto zwrócić uwagę, że przy tej uproszczonej interpretacji pomijamy istotną informację pochodzącą od zespolonego skierowania współrzędnych stanu
Warto zwrócić uwagę, że przy tej uproszczonej interpretacji pomijamy istotną informację pochodzącą od zespolonego skierowania współrzędnych stanu 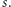
Przystąpimy teraz do krótkiej analizy dostępnych operacji na komputerze kwantowym, które odpowiadają odwracalnym operatorom 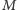 zachowującym długości wektorów (czyli dla każdego
zachowującym długości wektorów (czyli dla każdego 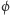 ma być
ma być 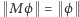 ). Operacje te nazywamy operatorami unitarnymi. Dla liczby naturalnej
). Operacje te nazywamy operatorami unitarnymi. Dla liczby naturalnej 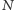 przez
przez 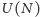 oznaczać będziemy grupę przekształceń unitarnych przestrzeni
oznaczać będziemy grupę przekształceń unitarnych przestrzeni 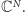 Jak łatwo się przekonać (zachęcamy do próby udowodnienia tego faktu) grupa ta może być utożsamiona ze zbiorem macierzy
Jak łatwo się przekonać (zachęcamy do próby udowodnienia tego faktu) grupa ta może być utożsamiona ze zbiorem macierzy 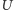 rozmiaru
rozmiaru 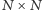 spełniających równość
spełniających równość 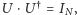 gdzie
gdzie 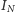 jest macierzą przekształcenia identycznościowego, a operacja
jest macierzą przekształcenia identycznościowego, a operacja 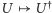 przyporządkowuje macierzy
przyporządkowuje macierzy ![[u ] i j](/math/temat/matematyka/algebra/2017/11/22/Jeszcze_o_algebrze_obliczen_kwantowych/12x-fa0ca5c64470c2abe47f372d239e80c614085aa2-im-33,33,33-FF,FF,FF.gif) macierz
macierz ![|[u-], ji](/math/temat/matematyka/algebra/2017/11/22/Jeszcze_o_algebrze_obliczen_kwantowych/13x-fa0ca5c64470c2abe47f372d239e80c614085aa2-im-33,33,33-FF,FF,FF.gif) np:
np:
![1- 1+ i 1− i 1- 1− i 1+ i 1-1 +i 1− i 1- 1− i 1+ i 1 0 2 [1− i 1+ i] = 2 [1+ i 1− i] oraz2 [1 −i 1+ i]⋅2 [1+ i 1− i] = [0 1]](/math/temat/matematyka/algebra/2017/11/22/Jeszcze_o_algebrze_obliczen_kwantowych/14x-fa0ca5c64470c2abe47f372d239e80c614085aa2-dm-33,33,33-FF,FF,FF.gif)
Iloczyn tensorowy.
W celu zwięzłego zapisu bramek kwantowych dużych rozmiarów wykorzystuje się operację tak zwanego iloczynu tensorowego. Iloczynem tensorowym przestrzeni wektorowych 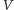 i
i 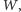 oznaczanym
oznaczanym 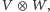 nazwiemy przestrzeń generowaną przez elementy
nazwiemy przestrzeń generowaną przez elementy 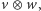 dla
dla 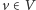 i
i 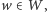 spełniające liniowe zależności
spełniające liniowe zależności

dla 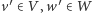 i
i 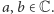 Można wykazać, że dla ustalonych baz
Można wykazać, że dla ustalonych baz 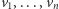 i
i 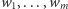 bazą przestrzeni
bazą przestrzeni 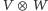 są elementy
są elementy 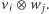
Powyższe zależności oznaczają, że 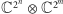 może być utożsamione z przestrzenią
może być utożsamione z przestrzenią 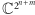 za pomocą przyporządkowania określonego w bazach Diraca przy użyciu formuły
za pomocą przyporządkowania określonego w bazach Diraca przy użyciu formuły 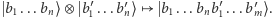
Operacja iloczynu tensorowego może być również wykonana na operatorach 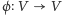 i
i 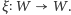 Jest ona oznaczana przez
Jest ona oznaczana przez 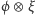 i zdefiniowana za pomocą formuły
i zdefiniowana za pomocą formuły

Intuicyjnie, każdy z operatorów w iloczynie tensorowym działa "niezależnie" na mniejszym podzbiorze współrzędnych.
Okazuje się (ponownie zachęcamy do próby samodzielnego udowodnienia tego faktu), że jeżeli 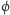 i
i 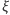 zadane są odpowiednio przez macierze
zadane są odpowiednio przez macierze 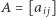 oraz
oraz ![|B = [bkm]](/math/temat/matematyka/algebra/2017/11/22/Jeszcze_o_algebrze_obliczen_kwantowych/4x-71ca61684a8b6675db8a9d3759895a1c807bd73a-im-33,33,33-FF,FF,FF.gif) to
to 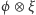 zadane jest przez macierz
zadane jest przez macierz 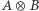 zdefiniowaną następująco:
zdefiniowaną następująco:

Na przykład:
![⎡⎢1 1 1 1⎤⎥ --1 1 1 -1- 1 1 1⎢⎢1 −1 1 −1⎥⎥ √ 2-[1 −1]⊗ √2-[1 −1] = 2⎢⎢1 1 −1 −1⎥⎥ . ⎢⎢ ⎥⎥ ⎣1 −1 −1 1⎦](/math/temat/matematyka/algebra/2017/11/22/Jeszcze_o_algebrze_obliczen_kwantowych/8x-71ca61684a8b6675db8a9d3759895a1c807bd73a-dm-33,33,33-FF,FF,FF.gif)