O zastosowaniach Combinatorial Nullstellensatz
Zadanie 6 z 48. Międzynarodowej Olimpiady Matematycznej (IMO) z 2007 roku było jednym z najtrudniejszych w historii Międzynarodowej Olimpiady Matematycznej.

Oto treść zadania.
Zadanie. Niech 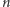 będzie dodatnią liczbą naturalną. Przyjmijmy, że
będzie dodatnią liczbą naturalną. Przyjmijmy, że

jest zbiorem 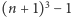 punktów w przestrzeni trójwymiarowej. Wyznacz najmniejszą możliwą liczbę płaszczyzn, których suma mnogościowa zawiera
punktów w przestrzeni trójwymiarowej. Wyznacz najmniejszą możliwą liczbę płaszczyzn, których suma mnogościowa zawiera 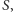 ale do której nie należy
ale do której nie należy 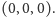
Zadanie rozwiązało tylko pięciu zawodników: Konstantin Matwiejew z Rosji, Peter Scholze z Niemiec, Danylo Radczenko z Ukrainy, Iurie Boreico z Mołdawii i Pietro Verteci z Włoch. W zasadzie tylko znajomość twierdzenia Combinatorial Nullstellensatz (kombinatoryczne twierdzenie o rozmieszczeniu zer, nawiązujące do twierdzenia Hilberta o zerach), któremu poświęcony jest ten artykuł, umożliwiała szybkie rozwiązanie zadania. Noga Alon opublikował swój artykuł Combinatorial Nullstellensatz [1] w 1999 roku, a już w 2007 roku kilku uczestników IMO stosowało metodę w nim opisaną. Wspomniane twierdzenie jest naturalnym uogólnieniem dobrze znanego uczniom twierdzenia, że wielomian jednej zmiennej stopnia 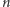 o współczynnikach rzeczywistych ma co najwyżej
o współczynnikach rzeczywistych ma co najwyżej  pierwiastków rzeczywistych, a jego treść jest następująca:
pierwiastków rzeczywistych, a jego treść jest następująca:
Twierdzenie (Combinatorial Nullstellensatz). Niech 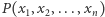 będzie niezerowym wielomianem
będzie niezerowym wielomianem  zmiennych stopnia
zmiennych stopnia 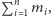 w którym współczynnik przy
w którym współczynnik przy 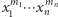 jest różny od zera. Wówczas dla dowolnych zbiorów
jest różny od zera. Wówczas dla dowolnych zbiorów  spełniających warunki
spełniających warunki 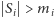 dla
dla 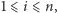 istnieją takie
istnieją takie 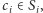 że
że 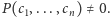
Dowód. Przeprowadzimy indukcję ze względu na stopień wielomianu 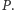 Nietrudny dowód początku indukcji
Nietrudny dowód początku indukcji 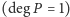 pozostawiam Czytelnikowi Spragnionemu Ćwiczeń jako ćwiczenie.
pozostawiam Czytelnikowi Spragnionemu Ćwiczeń jako ćwiczenie.
Załóżmy teraz, że 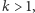 oraz że teza zachodzi dla wszystkich wielomianów stopnia niższego niż
oraz że teza zachodzi dla wszystkich wielomianów stopnia niższego niż 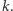 Niech wielomian
Niech wielomian 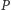 ma stopień
ma stopień 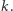 Bez straty ogólności można przyjąć, że
Bez straty ogólności można przyjąć, że 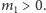 Wybierzmy
Wybierzmy 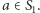 Podobnie, jak w przypadku wielomianów jednej zmiennej, możemy podzielić wielomian
Podobnie, jak w przypadku wielomianów jednej zmiennej, możemy podzielić wielomian 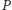 przez wielomian
przez wielomian 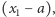 otrzymując
otrzymując

gdzie 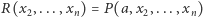 jest wielomianem
jest wielomianem 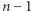 zmiennych, natomiast
zmiennych, natomiast 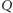 musi zawierać nieznikający jednomian postaci
musi zawierać nieznikający jednomian postaci 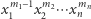 oraz
oraz  Dla dowodu nie wprost załóżmy, że wielomian
Dla dowodu nie wprost załóżmy, że wielomian 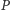 nie spełnia tezy. Wówczas dla dowolnych
nie spełnia tezy. Wówczas dla dowolnych 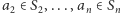 zachodzi równość
zachodzi równość 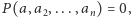 co oznacza, że także
co oznacza, że także 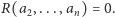
Wybierzmy teraz dowolnie 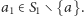 Otrzymujemy równości:
Otrzymujemy równości:

Ponieważ 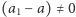 oraz
oraz 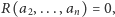 więc
więc 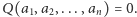 Wielomian
Wielomian 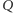 ma stopień
ma stopień 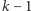 i niezerowy współczynnik przy
i niezerowy współczynnik przy 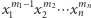 oraz przyjmuje wartość zero dla wszystkich
oraz przyjmuje wartość zero dla wszystkich 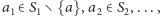
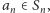 co jest sprzeczne z założeniem indukcyjnym. Uzyskana sprzeczność kończy dowód indukcyjny.
co jest sprzeczne z założeniem indukcyjnym. Uzyskana sprzeczność kończy dowód indukcyjny.
Poniżej przedstawię zastosowania Combinatorial Nullstellensatz do zadań olimpijskich, aby w końcu pokazać rozwiązanie zadania z IMO z 2007 roku, które było pretekstem do opowiedzenia o tej metodzie.
Zadanie (Rosja 2007). W każdy wierzchołek wypukłego 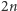 -kąta wpisano dwie różne liczby rzeczywiste. Udowodnić, że można z każdego wierzchołka usunąć po jednej liczbie w taki sposób, aby liczby w każdych dwóch sąsiednich wierzchołkach były różne.
-kąta wpisano dwie różne liczby rzeczywiste. Udowodnić, że można z każdego wierzchołka usunąć po jednej liczbie w taki sposób, aby liczby w każdych dwóch sąsiednich wierzchołkach były różne.
Dowód. Niech 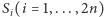 będzie dwuelementowym zbiorem liczb wpisanych w
będzie dwuelementowym zbiorem liczb wpisanych w 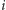 -ty wierzchołek. Określmy wielomian
-ty wierzchołek. Określmy wielomian 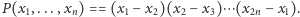 Wielomian
Wielomian 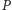 jest stopnia
jest stopnia 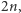 współczynnik przy wyrażeniu
współczynnik przy wyrażeniu 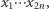 które jest stopnia
które jest stopnia 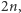 jest równy
jest równy 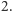 Na podstawie Combinatorial Nullstellensatz istnieją
Na podstawie Combinatorial Nullstellensatz istnieją 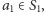
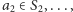
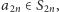 takie że
takie że 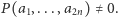 To oznacza, że każda z różnic:
To oznacza, że każda z różnic: 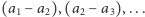 ,
, 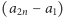 jest różna od 0, czyli istnieje taki wybór liczb ze zbiorów
jest różna od 0, czyli istnieje taki wybór liczb ze zbiorów 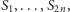 że
że 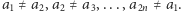
Zadanie (5th NIMO Winter Contest 2014). Zdefiniujmy taką funkcję 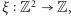 że
że 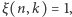 gdy
gdy 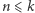 oraz
oraz 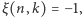 gdy
gdy 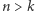 i zdefiniujmy wielomian
i zdefiniujmy wielomian

Wyznacz współczynnik przy 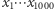 w wielomianie
w wielomianie 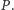
Rozwiązanie. Zauważmy, że wielomian 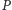 jest stopnia
jest stopnia 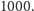 Załóżmy, że współczynnik przy
Załóżmy, że współczynnik przy 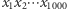 jest różny od
jest różny od 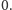 Zdefiniujmy zbiory
Zdefiniujmy zbiory 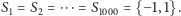 Wówczas korzystając z Combinatorial Nullstellensatz, otrzymujemy takie elementy
Wówczas korzystając z Combinatorial Nullstellensatz, otrzymujemy takie elementy 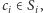 gdzie
gdzie 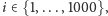 że
że 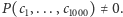 Z drugiej strony sumy częściowe
Z drugiej strony sumy częściowe 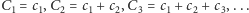 definiują pewien "spacer po liczbach całkowitych", kończący się na
definiują pewien "spacer po liczbach całkowitych", kończący się na 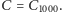 Liczba
Liczba 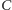 musi być parzysta, dlatego spacer ten w pewnym momencie osiągnie
musi być parzysta, dlatego spacer ten w pewnym momencie osiągnie 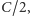 zatem dla pewnego
zatem dla pewnego 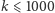 zachodzi
zachodzi 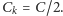 Oznacza to jednak, że
Oznacza to jednak, że 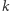 -ty czynnik w definicji wielomianu
-ty czynnik w definicji wielomianu 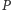 wynosi 0, co przeczy stwierdzeniu
wynosi 0, co przeczy stwierdzeniu 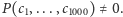 Zatem współczynnik przy
Zatem współczynnik przy 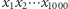 musi być równy
musi być równy 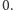
Przejdziemy teraz do rozwiązania przytoczonego na początku artykułu zadania 6 z IMO 2007, które jest trudniejsze niż poprzednie zadania.
Rozwiązanie (Danylo Radczenko). Niech 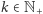 i
i 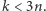 Weźmy
Weźmy 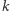 parami różnych płaszczyzn, których suma mnogościowa zawiera zbiór
parami różnych płaszczyzn, których suma mnogościowa zawiera zbiór 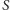 i żadna z tych płaszczyzn nie przechodzi przez punkt
i żadna z tych płaszczyzn nie przechodzi przez punkt 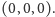 Niech
Niech 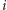 -ta płaszczyzna będzie określona równaniem
-ta płaszczyzna będzie określona równaniem 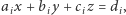 gdzie
gdzie 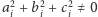 oraz
oraz 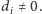 Rozważmy wielomian
Rozważmy wielomian 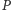 postaci
postaci
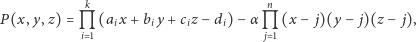 |
gdzie 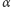 jest tak dobrane, że
jest tak dobrane, że 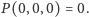 Wielomian
Wielomian 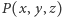 przyjmuje wartość 0 dla każdego elementu należącego do zbioru
przyjmuje wartość 0 dla każdego elementu należącego do zbioru 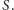 Dla
Dla 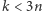 współczynnik przy
współczynnik przy 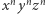 nie jest równy
nie jest równy 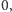 gdyż jest równy
gdyż jest równy 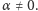 Dla zbiorów
Dla zbiorów 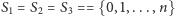 zachodzą warunki:
zachodzą warunki: 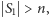
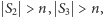 więc na podstawie Combinatorial Nullstellensatz istnieje taki punkt
więc na podstawie Combinatorial Nullstellensatz istnieje taki punkt 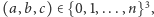 że
że 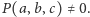 Zatem istnieje punkt
Zatem istnieje punkt 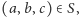 dla którego
dla którego 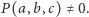 Otrzymaliśmy sprzeczność. Wobec tego
Otrzymaliśmy sprzeczność. Wobec tego 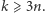
Wystarczy jeszcze wskazać przykład 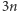 płaszczyzn, które spełniają warunki zadania. Są nimi
płaszczyzn, które spełniają warunki zadania. Są nimi

Powyższe zadanie jest pewną wariacją na temat problemu, jaki postawił Peter Komjáth: ile potrzeba hiperpłaszczyzn, aby pokryć wszystkie, z wyjątkiem jednego, wierzchołki kostki jednostkowej w przestrzeni 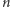 -wymiarowej. Rozwiązanie tego problemu pojawiło się przed 1993 rokiem, ale dopiero Noga Alon i Zoltan Füredi w 1993 roku w pracy [2] przedstawili krótkie i eleganckie rozumowanie. Poniższy dowód pochodzi z pracy [1].
-wymiarowej. Rozwiązanie tego problemu pojawiło się przed 1993 rokiem, ale dopiero Noga Alon i Zoltan Füredi w 1993 roku w pracy [2] przedstawili krótkie i eleganckie rozumowanie. Poniższy dowód pochodzi z pracy [1].
Twierdzenie. Niech 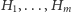 będzie rodziną hiperpłaszczyzn w
będzie rodziną hiperpłaszczyzn w 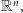 których suma zawiera wszystkie, z wyjątkiem jednego, wierzchołki kostki jednostkowej, czyli zbiór
których suma zawiera wszystkie, z wyjątkiem jednego, wierzchołki kostki jednostkowej, czyli zbiór 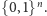 Wówczas
Wówczas 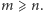
Dowód. Bez straty ogólności możemy przyjąć, że usuniętym wierzchołkiem jest punkt 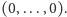 Niech hiperpłaszczyzna
Niech hiperpłaszczyzna 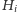 dana będzie równaniem
dana będzie równaniem 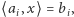 gdzie
gdzie 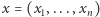 i
i 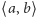 jest standardowym iloczynem skalarnym
jest standardowym iloczynem skalarnym 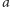 i
i 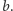 Dla każdego
Dla każdego 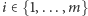 zachodzi warunek
zachodzi warunek 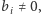 gdyż żadna z hiperpłaszczyzn nie przechodzi przez punkt
gdyż żadna z hiperpłaszczyzn nie przechodzi przez punkt 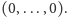 Załóżmy dla dowodu nie wprost, że
Załóżmy dla dowodu nie wprost, że 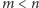 i zdefiniujmy wielomian
i zdefiniujmy wielomian

Wielomian 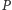 ma stopień
ma stopień 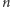 i współczynnik przy
i współczynnik przy 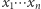 równy
równy

zatem różny od 0. Na podstawie Combinatorial Nullstellensatz dla 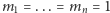 oraz
oraz 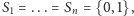 istnieje taki punkt
istnieje taki punkt 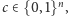 że
że 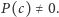 Punkt
Punkt  jest różny od
jest różny od 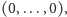 gdyż wielomian
gdyż wielomian 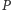 przyjmuje wartość 0 dla
przyjmuje wartość 0 dla 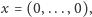 a zatem punkt
a zatem punkt  należy do zadanego zbioru i nie należy do żadnej z hiperpłaszczyzn. Otrzymaliśmy sprzeczność, wobec tego
należy do zadanego zbioru i nie należy do żadnej z hiperpłaszczyzn. Otrzymaliśmy sprzeczność, wobec tego 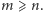 Teraz wystarczy wskazać
Teraz wystarczy wskazać 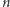 hiperpłaszczyzn spełniających warunki zadania; są one zadane równaniami
hiperpłaszczyzn spełniających warunki zadania; są one zadane równaniami 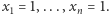

Mam nadzieję, że powyższe przykłady przekonały Cię, Drogi Czytelniku, o użyteczności Combinatorial Nullstellensatz w rozwiązywaniu problemów z pozoru z nim niezwiązanych. Na zakończenie chciałbym zauważyć, że to wspaniałe twierdzenie jest słuszne dla wielomianów o współczynnikach z dowolnego ciała. Dotychczas używaliśmy jedynie ciała liczb rzeczywistych. Drugim w kolejności naturalnym wyborem ciała jest ciało 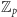 - ciało reszt z dzielenia przez liczbę pierwszą
- ciało reszt z dzielenia przez liczbę pierwszą 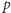 z dodawaniem i mnożeniem modulo
z dodawaniem i mnożeniem modulo 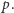 Zastosowanie Combinatorial Nullstellensatz w tej sytuacji prowadzi do niezwykle eleganckich dowodów bardzo pięknych twierdzeń z teorii liczb. Niestety, w tym artykule brakuje już miejsca na przedstawienie przykładów, obiecuję jednak zaprezentować je w numerze wrześniowym w nadziei, że oczekiwanie zaostrzy apetyt nie tylko Czytelnika Bardzo Zainteresowanego.
Zastosowanie Combinatorial Nullstellensatz w tej sytuacji prowadzi do niezwykle eleganckich dowodów bardzo pięknych twierdzeń z teorii liczb. Niestety, w tym artykule brakuje już miejsca na przedstawienie przykładów, obiecuję jednak zaprezentować je w numerze wrześniowym w nadziei, że oczekiwanie zaostrzy apetyt nie tylko Czytelnika Bardzo Zainteresowanego.