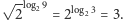Intuicjonizm i to, co po nim
Udowodnijmy lub obalmy twierdzenie: istnieją takie liczby niewymierne 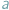 i
i 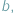 że
że 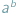 jest liczbą wymierną.
jest liczbą wymierną.
Rozważmy liczbę 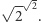 Jeśli jest ona wymierna, szukanymi liczbami są
Jeśli jest ona wymierna, szukanymi liczbami są 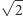 i
i 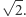 Jeśli natomiast
Jeśli natomiast 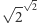 jest niewymierna, to wraz z nią szukaną liczbą jest
jest niewymierna, to wraz z nią szukaną liczbą jest 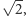 bowiem
bowiem 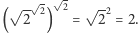
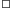
Tego rodzaju dowód ma szczególną cechę: dowodzimy istnienia jakichś obiektów, nie umiejąc stwierdzić "co one za jedne". Patrząc głębiej, widzimy, że wykorzystaliśmy tu tzw. zasadę wyłączonego środka: liczba 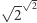 jest wymierna albo jest niewymierna.
jest wymierna albo jest niewymierna.
Pojawianie się, począwszy od drugiej połowy XIX wieku, sytuacji krępujących matematyków, obiektów, których własności były nadmiernie paradoksalne, skłoniło część z nich (podpuszczaną zresztą przez Poincarégo) do narzucenia sobie (i zalecenia innym) ostrożności w dowodzeniu zwłaszcza istnienia jakichś obiektów: dowody 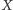 istnieje, bo gdyby nie istniał, to olaboga! zostały wykluczone. Nurt, którego ojcem założycielem okrzyknięto Luitzena Brouwera, nazwano intuicjonizmem. Jego rozwój przysporzył matematyce takich pojęć, jak funkcje obliczalne, algorytmy, a nawet maszyna Turinga. Dziś intuicjonizm, pod nazwą konstruktywizmu jest filozoficznym aspektem informatyki, ale to już inna historia.
istnieje, bo gdyby nie istniał, to olaboga! zostały wykluczone. Nurt, którego ojcem założycielem okrzyknięto Luitzena Brouwera, nazwano intuicjonizmem. Jego rozwój przysporzył matematyce takich pojęć, jak funkcje obliczalne, algorytmy, a nawet maszyna Turinga. Dziś intuicjonizm, pod nazwą konstruktywizmu jest filozoficznym aspektem informatyki, ale to już inna historia.
Dowiedźmy jednak początkowe twierdzenie zgodnie z intuicjonistami: takimi liczbami są 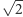 i
i 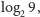 bo
bo