Co by było, gdybyśmy, porwani przez jakichś wrogich, a potężnych Marsjan, zostali postawieni w takiej sytuacji: ludzkość zostanie ocalona, jeśli wykażemy się odpowiednią inteligencją matematyczną i, dysponując jedynie kartką papieru i ołówkiem, obliczymy w ciągu jednego dnia wartość 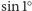z dokładnością do 10 cyfr po przecinku? Kto z absolwentów liceów poradziłby sobie z takim wyzwaniem? Chyba niewielu Czytelników potrafiłoby aż z taką dokładnością wyznaczyć poprawną wartość: 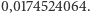Na pewno nie za pomocą cyrkla, linijki i ołówka. Zresztą podobnie trudno by było, gdyby ci podli Marsjanie kazali nam obliczyć np. 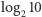czy 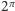z tą samą dokładnością. Powstaje pytanie: jak sobie radzili z tymi problemami nasi poprzednicy, którzy wieki temu drukowali tabele różnych funkcji matematycznych: pierwiastków, sinusów i logarytmów z zaskakująco dobrymi dokładnościami, sięgającymi nieraz 8 cyfr znaczących?

Dochodzimy tu do drugiej niezwykłej własności wielomianów. Otóż, o czym dowiadują się studenci pierwszego roku kierunków ścisłych, wielomiany mają jeszcze jedną sympatyczną własność. Za ich pomocą możemy dowolnie dokładnie przybliżać wszystkie funkcje dostatecznie gładkie, czyli takie, których wykres jest linią ciągłą bez żadnych załamań (konkretnie funkcje klasy 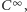czyli nieskończenie wiele razy różniczkowalne), a do nich należą właśnie funkcje trygonometryczne, logarytmy, funkcje wykładnicze. Konkretnie: w każdym skończonym przedziale możemy tak dobrać współczynniki wielomianu, żeby wartości w tym przedziale różniły się od wartości interesującej nas funkcji o mniej, niż z góry zadana wartość. Dla funkcji sinus i dla przedziału wystarczy wziąć wielomian

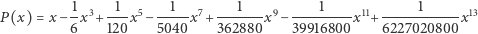
(w tym wzorze w mianownikach mamy silnie wykładników, a 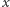jest podane w mierze łukowej), aby otrzymać wartości 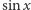z dokładnością do 10 cyfr dziesiętnych po przecinku dla każdego z tego przedziału. Znając ten wzór i dysponując paroma godzinami, na pewno byśmy sobie z marsjańskim problemem poradzili.

No to do roboty! Jak jednak wyznaczyć wiele wartości wielomianu tak, aby się jak najmniej napracować? Postawmy się w sytuacji autora tabel matematycznych dwa wieki temu - nie mamy komputerów, chcemy osiągnąć dużą dokładność i obliczyć wartości takiej funkcji, jak sinus, powiedzmy, co 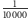radiana. Ile trzeba będzie wykonać mnożeń? One w końcu sprawiają więcej kłopotu niż dodawanie i odejmowanie. 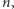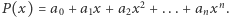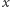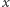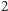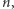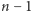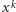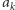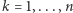Powiedzmy, że zajmiemy się wielomianem stopnia postaci Na pierwszy rzut oka wygląda na to, że dla każdej wartości trzeba obliczyć wszystkie potęgi od do co kosztuje mnożeń, potem otrzymane wartości przemnożyć przez współczynniki dla (kolejne mnożeń) i uzyskane liczby zsumować. Razem mamy więc 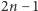mnożeń i 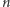dodawań.

Dość łatwo można ten wynik poprawić, stosując schemat Hornera. Jeśli przedstawimy nasz wielomian w postaci

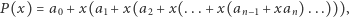
wówczas - o dziwo! - liczba mnożeń spadnie nam do 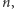a liczba dodawań się nie zmieni. W tej metodzie obliczenia zaczynamy od wewnątrz: mnożymy 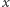przez 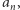dodajemy 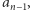mnożymy przez 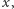dodajemy 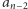itd., aż dodamy na końcu 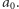Wydaje się, że tego wyniku poprawić już nie można.

A jednak! Przedstawimy teraz sposób, za pomocą którego będziemy obliczali wartości wielomianu w kolejnych liczbach, nie wykonując, poza kilkoma początkowymi wartościami, żadnego mnożenia! Metodę zilustrujemy na przykładzie konkretnego wielomianu 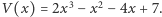Będziemy wyznaczali wartości tego wielomianu dla kolejnych liczb naturalnych. Pierwsze cztery wartości to, dla 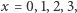odpowiednio 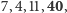co obliczamy w pamięci lub schematem Hornera.

Teraz pora na magię. Obliczmy różnice między tymi wartościami: będą to kolejno liczby 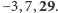Powtórzmy to jeszcze raz, tym razem dla tych trzech wartości: 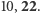Na koniec jeszcze raz obliczmy różnicę między tymi dwiema wartościami: 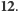Zapamiętajmy tę wartość, będziemy z niej wielokrotnie korzystać. Jesteśmy już przygotowani do wyznaczenia wartości 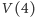za pomocą 3 dodawań. Skupiamy się na ostatnich wartościach z przedstawionych tutaj ciągów, zapisanych w odwrotnej kolejności, czyli 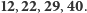Dalsze trzy wartości otrzymamy, sumując je w następujący sposób: 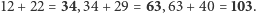Ostatnia otrzymana wartość to właśnie 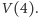Teraz, żeby otrzymać 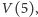powtarzamy nasz algorytm dla właśnie wygenerowanych liczb, zaczynając od tej samej dwunastki, co poprzednio i dostajemy kolejno 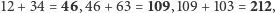więc 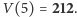Biorąc znowu dwunastkę i sumując ostatnio otrzymane wyniki, otrzymamy kolejno wartości 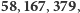z których ostatnia liczba jest, jak się już domyślamy, równa 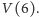Następnie tą samą metodą wyznaczamy po kolei 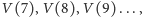za każdym razem wykonując tylko trzy dodawania i żadnego mnożenia!

Co się tu dzieje? Wszystko dzięki niepozornemu operatorowi różnicy skończonej, który oznaczymy przez 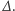Ten operator działa na wielomianach i tworzy z nich nowe wielomiany według następującego wzoru: 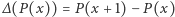dla dowolnego wielomianu 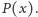Czyli dla każdego argumentu wartość 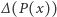jest równa przyrostowi wartości wielomianu, gdy argument zwiększymy o 1. Obliczmy zatem dla naszego wielomianu

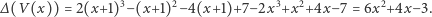Okazuje się, że otrzymaliśmy wielomian stopnia o jeden niższego niż oryginał. Chwila zastanowienia i widzimy, że tak będzie dla każdego wielomianu trzeciego stopnia. Operator 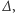działając na taki wielomian, zmniejszy jego stopień do kwadratowego. I ogólnie, jeśli wielomian 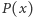jest stopnia 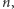to 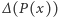będzie wielomianem stopnia 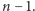Można to sprawdzić, rozwijając 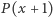ze wzoru dwumianowego Newtona; współczynnik przy najwyższej potędze to 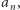więc wyraz z 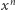skróci się przy odjęciu 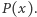Jeszcze krótki namysł i zobaczymy, że współczynnikiem przy najwyższej potędze (czyli przy 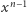) wielomianu 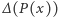będzie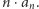

Wprowadźmy teraz potęgi operatora 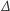ze względu na składanie. Ustalmy, że 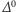jest operatorem identycznościowym, czyli z definicji 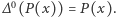Przyjmijmy, że 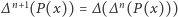dla 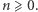Co się stanie, jeśli będziemy iterować operator 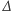dla wielomianu 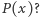Pierwsza iteracja - to już wiemy - będzie wielomianem stopnia 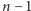o współczynniku przy najwyższej potędze równym 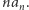Druga - wielomianem stopnia 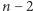z najwyższym współczynnikiem równym 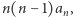trzecia da nam wielomian stopnia 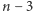o najwyższym współczynniku równym 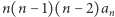i tak dalej, aż w końcu 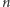-ta iteracja, czyli 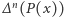będzie wielomianem stopnia zerowego o współczynniku przy najwyższej potędze (czyli wyrazie stałym) równym 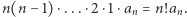Zatem postać wielomianu 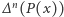zależy jedynie od stopnia tego wielomianu i od współczynnika 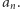Jest więc dość łatwa do wyliczenia. Przykładowo, dla naszego wielomianu 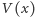mamy

• 
• 
• 
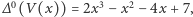
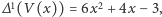
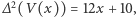
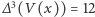• (co było do przewidzenia od samego początku, bo )

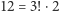i kolejne iteracje 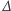dadzą już tylko wielomiany zerowe. Teraz pora na najważniejsze. Widzimy, że bezpośrednio z definicji operatora 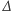wynika wzór

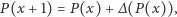
co zapiszemy w dogodniejszej dla dalszych rozważań postaci

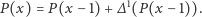
Ale 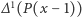to też wielomian zmiennej 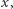więc proces możemy iterować, bo w szczególności 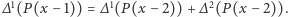Idąc tak dalej, otrzymujemy

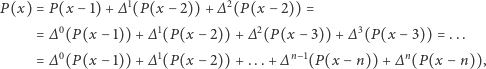
a ostatni wyraz, jak wiemy, równy jest 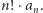Widać więc, że do wyznaczenia wartości 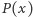wystarczy do wartości 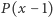dodać wartości wszystkich 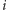-tych potęg 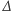dla argumentów gdzie 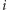przebiega zbiór 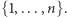A te wartości możemy wyznaczać kolejno, wykonując dodawań.

Stwórzmy więc dla naszego wielomianu 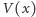tabelę takich wartości. Zaczniemy od obliczenia "na piechotę" wartości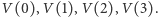

Obliczmy teraz wartości 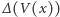dla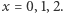

Następnie wyznaczmy wartości 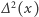dla 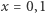; więcej nam nie potrzeba. Od razu wstawmy dla porządku 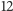w miejsce 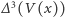dla 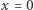- wiemy, że będzie to 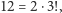ale gdybyśmy nie dowierzali, zawsze możemy tę wartość uzyskać z ostatniej wypełnionej kolumny, odejmując 10 od 22.

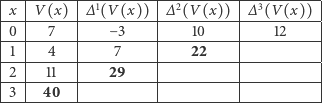W powyższej tabeli została wytłuszczona przekątna, za pomocą której będziemy generowali kolejną przekątną. Zaczniemy od domyślnej dwunastki w ostatniej kolumnie (cała kolumna składa się z samych dwunastek), którą wstawimy dla 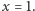Teraz, poczynając od góry, będziemy do każdego z wytłuszczonych elementów przekątnej dodawali jego prawego sąsiada i wynik zapisywali pod spodem, wytłuszczając go:

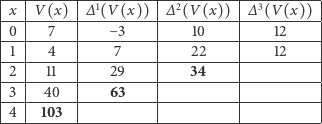Proszę! Wykonaliśmy trzy dodawania i mamy wartość 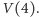Jedziemy dalej:

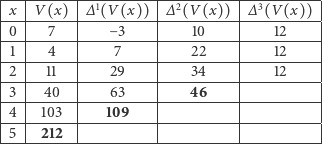I jeszcze 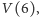skoro nam tak dobrze idzie:

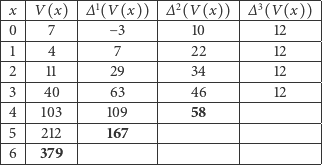Działa! Trzy dodawania i mamy obliczoną kolejną wartość wielomianu trzeciego stopnia.

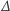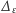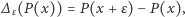No dobra. To było proste, ale mieliśmy sytuację komfortową, kiedy to wartości wielomianu obliczaliśmy dla kolejnych liczb naturalnych. Co by jednak było, gdyby argumenty były wymierne? Otóż nic by się nie zmieniło. Okazuje się, że jeśli operator zastąpimy operatorem dla dowolnego wymiernego dodatniego i zdefiniujemy to zachowamy podstawową cechę operatora 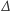: zastosowanie tego operatora zmniejsza stopień wielomianu o 1. To nam wystarcza do tego, żeby powtórzyć naszą procedurę dla dowolnego początkowego i dla dowolnego 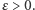Obliczenie kolejnych 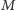wartości dla argumentów różniących się o z góry ustaloną stałą dla dowolnego wielomianu stopnia wymaga zatem obliczenia jego kolejnych wartości "na piechotę", a następnie zastosowania 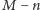razy naszego schematu, za każdym razem wymagającego jedynie 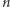dodawań, bez wykonywania jakiegokolwiek mnożenia! Niewiarygodne!

Na to, żeby metodę opisaną powyżej wykorzystać do budowy maszyny, przypuszczalnie wpadł jako pierwszy inżynier heskiej armii Johann Helfrich von Müller (1742-1830). Pomysł ten rozwinął i częściowo zrealizował angielski matematyk Charles Babbage (1791-1871). Jest to bohater niezwykły, wizjoner, twórca modelu komputera w postaci, której praktycznie dziś powszechnie używamy. Żył długo, choć jego życie nie było usłane różami. Dość młodo został profesorem matematyki w Cambridge, głównie za prace w dziedzinie kryptografii - ciągnęło go zawsze w kierunku zastosowań matematyki w informatyce, choć informatyki wtedy jeszcze nie było. W latach 20. XIX wieku wpadł na pomysł skonstruowania maszyny, która wykonywałaby automatycznie działania prowadzące do wyznaczania kolejnych wartości wielomianów według podanej wyżej metody. Sam mechanizm arytmometru był znany od prawie 200 lat dzięki konstrukcjom Schickarda, Pascala i Leibniza. Chodziło o to, żeby ustawić kilka arytmometrów tak, aby mogły sobie nawzajem przekazywać obliczone sumy w odpowiedniej kolejności. Efektem prac Babbage'a była maszyna różnicowa, której model przedstawiony jest na zdjęciu powyżej. Wymagała ona ręcznego wykonania początkowych czynności. Babbage na tym nie poprzestał. Zaczął budowę kolejnej wersji maszyny różnicowej, która byłaby znacznie większa i... nigdy jej nie ukończył. Nie dlatego, żeby napotkał jakieś nieoczekiwane przeszkody. Po prostu w trakcie prac nad nią wpadł na pomysł, który tak go pochłonął, że zarzucił zaczęte prace. Ale jest to temat na osobną historię.