Co to jest?
Liczby zespolone i kwaterniony
Tak jak problemy praktyczne prowadzą do równań, tak równania prowadzą czasem do nowych rodzajów liczb. Ambitny kmieć z czasów Mieszka I, będący właścicielem trzech krów i marzący o nabyciu (lub zdobyciu) dodatkowych sztuk bydła tak, by stać się szanowanym posiadaczem tuzina krów, musiał niewątpliwie rozwiązywać zadanie matematyczne, które dziś zapisujemy równaniem 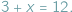 Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie
Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie 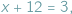 które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...
które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...
Równanie to ma jednak sens praktyczny: opisuje stan posiadania pewnego mieszkańca sąsiedniej wioski przed i po spełnieniu marzeń naszego kmiecia. Żeby to równanie rozwiązać, potrzebne są nowe liczby - tu są to liczby ujemne. W tak powiększonym zbiorze liczb, zwanym zbiorem liczb całkowitych, każde równanie postaci 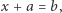 gdzie
gdzie  i
i 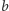 to liczby całkowite, ma rozwiązanie.
to liczby całkowite, ma rozwiązanie.
Żeby rozwiązać równanie 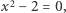 nie wystarczą nie tylko liczby całkowite, ani nawet wszystkie liczby wymierne, czyli ułamki
nie wystarczą nie tylko liczby całkowite, ani nawet wszystkie liczby wymierne, czyli ułamki 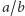 zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną
zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną 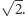
Dlaczego nie wystarczy dołączyć samej liczby 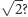 Bo pojedyncze liczby są tak mało użyteczne, że nawet nie zasługują na uwagę. W istocie, na pytanie co to jest liczba? istnieje tylko jedna, matematycznie użyteczna, choć pozornie paradoksalna, odpowiedź: liczba to element zbioru, którego elementy można dodawać, odejmować, mnożyć i dzielić. Zakłada się przy tym, że działania te powinny spełniać pewne naturalne warunki, jak np. przemienność i łączność dodawania oraz mnożenia, istnienie odwrotności każdej liczby różnej od zera itp., dobrze znane z algebry szkolnej. Zbiory liczb, spełniające te warunki, algebraicy nazywają ciałami.
Bo pojedyncze liczby są tak mało użyteczne, że nawet nie zasługują na uwagę. W istocie, na pytanie co to jest liczba? istnieje tylko jedna, matematycznie użyteczna, choć pozornie paradoksalna, odpowiedź: liczba to element zbioru, którego elementy można dodawać, odejmować, mnożyć i dzielić. Zakłada się przy tym, że działania te powinny spełniać pewne naturalne warunki, jak np. przemienność i łączność dodawania oraz mnożenia, istnienie odwrotności każdej liczby różnej od zera itp., dobrze znane z algebry szkolnej. Zbiory liczb, spełniające te warunki, algebraicy nazywają ciałami.
Do zapisywania wyników pomiarów najlepiej nadaje się ciało liczb rzeczywistych 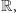 które można sobie wyobrażać jako zbiór wszystkich ułamków dziesiętnych, z (przeważnie) nieskończoną liczbą cyfr po przecinku. Prawdziwą naturę tych liczb dobrze oddaje definicja, pochodząca z jednego z najlepszych podręczników algebry: "Liczby rzeczywiste, cokolwiek by to nie było, mają następujące własności…" - tu następuje lista własności działań. Użyteczność liczb polega nie na tym, że każda z nich z osobna istnieje, lecz na tym, że możemy na nich działać.
które można sobie wyobrażać jako zbiór wszystkich ułamków dziesiętnych, z (przeważnie) nieskończoną liczbą cyfr po przecinku. Prawdziwą naturę tych liczb dobrze oddaje definicja, pochodząca z jednego z najlepszych podręczników algebry: "Liczby rzeczywiste, cokolwiek by to nie było, mają następujące własności…" - tu następuje lista własności działań. Użyteczność liczb polega nie na tym, że każda z nich z osobna istnieje, lecz na tym, że możemy na nich działać.
Zbiór liczb rzeczywistych jest dostatecznie duży, by można było w nim znaleźć rozwiązania bardzo wielu użytecznych równań, ale jednak nie wszystkich; na przykład równanie 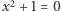 nie ma rozwiązań w zbiorze
nie ma rozwiązań w zbiorze 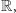 gdyż lewa strona tego równania jest dodatnia dla każdej liczby rzeczywistej
gdyż lewa strona tego równania jest dodatnia dla każdej liczby rzeczywistej 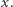 Ogólniej, z lekcji algebry pamiętamy, że równanie kwadratowe
Ogólniej, z lekcji algebry pamiętamy, że równanie kwadratowe 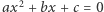 nie ma rozwiązań rzeczywistych, gdy
nie ma rozwiązań rzeczywistych, gdy 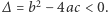
Zatem, gdy upieramy się przy tym, by równanie 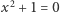 jednak miało rozwiązanie, musimy powiększyć zbiór
jednak miało rozwiązanie, musimy powiększyć zbiór 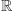 do większego ciała, które w szczególności będzie zawierać pierwiastek naszego równania - tradycyjnie oznaczymy go symbolem
do większego ciała, które w szczególności będzie zawierać pierwiastek naszego równania - tradycyjnie oznaczymy go symbolem 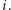 Jest to pierwsza litera słowa imaginary, czyli urojona, no bo przecież nie jest to liczba rzeczywista…Nasze nowe ciało powinno zatem zawierać
Jest to pierwsza litera słowa imaginary, czyli urojona, no bo przecież nie jest to liczba rzeczywista…Nasze nowe ciało powinno zatem zawierać 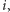 wszystkie "stare" liczby
wszystkie "stare" liczby 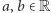 oraz wyniki działań na nich, a więc elementy postaci
oraz wyniki działań na nich, a więc elementy postaci 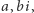 a także
a także 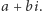 Zbiór wszystkich wyrażeń tej postaci oznaczamy symbolem
Zbiór wszystkich wyrażeń tej postaci oznaczamy symbolem 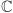 (complex numbers) i nazywamy liczbami zespolonymi.
(complex numbers) i nazywamy liczbami zespolonymi.
Liczby zespolone możemy w oczywisty sposób dodawać i odejmować:

Możemy je także mnożyć - w tym celu po prostu "otwieramy nawiasy":

a następnie korzystamy z podstawowej własności 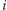 : jest to pierwiastek równania
: jest to pierwiastek równania 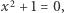 zatem
zatem 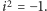 Podstawiając tę wartość do powyższej równości, otrzymujemy wzór
Podstawiając tę wartość do powyższej równości, otrzymujemy wzór

Zauważmy, że tak zdefiniowane działania rozszerzają znane nam działania dodawania, odejmowania i mnożenia liczb rzeczywistych, co łatwo sprawdzić podstawiając w powyższych wzorach 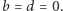 Trzy działania już mamy! A co z dzieleniem? Ponieważ dzielenie to mnożenie przez odwrotność dzielnika, wystarczy znaleźć odwrotność każdego elementu
Trzy działania już mamy! A co z dzieleniem? Ponieważ dzielenie to mnożenie przez odwrotność dzielnika, wystarczy znaleźć odwrotność każdego elementu 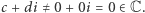 W tym celu zauważmy, że
W tym celu zauważmy, że 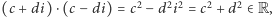 skąd
skąd

Zatem dzielenie liczb zespolonych jest także wykonalne. Tak stworzyliśmy ciało 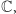 które zawiera wszystkie liczby rzeczywiste oraz urojoną liczbę
które zawiera wszystkie liczby rzeczywiste oraz urojoną liczbę 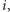 spełniającą równanie
spełniającą równanie 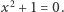
Sceptyczny Czytelnik może w tym miejscu wyrazić wątpliwość, czy warto było wykonywać tę całą pracę tylko po to, by uzyskać pierwiastek jednego konkretnego równania. W istocie nie jest aż tak źle; rozważmy dla przykładu równanie 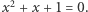 Mamy
Mamy 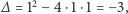 więc w szkole w tym miejscu przestalibyśmy zajmować się tym równaniem. Gdy jednak dopełnimy lewą stronę do pełnego kwadratu:
więc w szkole w tym miejscu przestalibyśmy zajmować się tym równaniem. Gdy jednak dopełnimy lewą stronę do pełnego kwadratu:

otrzymamy równanie

W ten sposób znaleźliśmy dwie liczby zespolone, które są pierwiastkami naszego równania. Podobnie będzie z każdym innym równaniem kwadratowym - w ciele 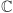 zawsze bez trudu znajdziemy jego pierwiastki.
zawsze bez trudu znajdziemy jego pierwiastki.

wikipedia
Carl Friedrich Gauss (1777-1855)
W istocie, jak udowodnił 22-letni Carl Friedrich Gauss w roku 1799, nie tylko każdy trójmian, ale także każdy wielomian dodatniego stopnia ma w ciele 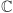 pierwiastek; jest to tak zwane Zasadnicze Twierdzenie Algebry. Jest to prawda także wtedy, gdy współczynniki naszego wielomianu są liczbami zespolonymi.
pierwiastek; jest to tak zwane Zasadnicze Twierdzenie Algebry. Jest to prawda także wtedy, gdy współczynniki naszego wielomianu są liczbami zespolonymi.
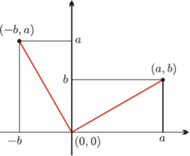
Ponieważ liczba zespolona 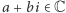 jest wyznaczona przez parę liczb rzeczywistych
jest wyznaczona przez parę liczb rzeczywistych 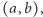 można ją interpretować jako punkt płaszczyzny kartezjańskiej
można ją interpretować jako punkt płaszczyzny kartezjańskiej 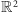 o współrzędnych
o współrzędnych 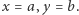 Wówczas podciało
Wówczas podciało 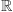 liczb rzeczywistych
liczb rzeczywistych 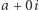 wypełnia oś
wypełnia oś 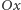 układu współrzędnych, zaś liczba urojona
układu współrzędnych, zaś liczba urojona 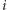 leży na osi
leży na osi 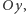 na wysokości 1.
na wysokości 1.
Dodawanie liczby zespolonej 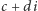 do dowolnego punktu płaszczyzny kartezjańskiej odpowiada w tej interpretacji przesunięciu go o wektor
do dowolnego punktu płaszczyzny kartezjańskiej odpowiada w tej interpretacji przesunięciu go o wektor ![|[c,d].](/math/temat/matematyka/algebra/2016/09/30/Liczby_zespolone_i_kwaterniony/2x-df1f21ff959dfa972788daf50e21ec7507343c1c-im-33,33,33-FF,FF,FF.gif) A jakim przekształceniem jest mnożenie przez liczbę
A jakim przekształceniem jest mnożenie przez liczbę 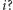 Dla dowolnego punktu
Dla dowolnego punktu 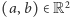 otrzymujemy
otrzymujemy

Zatem mnożenie przez 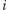 przenosi punkt
przenosi punkt 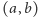 na punkt
na punkt 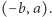 Łatwo dostrzec, że jest to obrót płaszczyzny wokół punktu
Łatwo dostrzec, że jest to obrót płaszczyzny wokół punktu 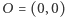 o kąt prosty, w kierunku przeciwnym do kierunku ruchu wskazówek zegara.
o kąt prosty, w kierunku przeciwnym do kierunku ruchu wskazówek zegara.
Ogólniej, jeśli punkt 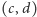 leży na okręgu jednostkowym o środku w punkcie
leży na okręgu jednostkowym o środku w punkcie 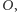 to liczba zespolona
to liczba zespolona 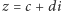 spełnia warunek
spełnia warunek

dla pewnego kąta 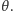
Wówczas mnożenie przez  jest obrotem płaszczyzny wokół punktu
jest obrotem płaszczyzny wokół punktu 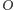 o kąt
o kąt 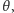 w kierunku przeciwnym do kierunku ruchu wskazówek zegara.
w kierunku przeciwnym do kierunku ruchu wskazówek zegara.
Na przykład, dla liczby 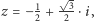 która pojawiła się wcześniej jako pierwiastek równania
która pojawiła się wcześniej jako pierwiastek równania 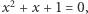 mamy
mamy 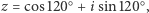 więc otrzymujemy obrót o
więc otrzymujemy obrót o 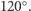 Trzykrotne wykonanie tego obrotu doprowadzi nas zatem do punktu wyjścia; nie powinno to być zaskoczeniem, skoro przekształcenie to odpowiada mnożeniu przez
Trzykrotne wykonanie tego obrotu doprowadzi nas zatem do punktu wyjścia; nie powinno to być zaskoczeniem, skoro przekształcenie to odpowiada mnożeniu przez 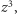 zaś
zaś 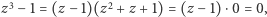 skąd
skąd 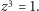
Widzimy zatem, że liczby zespolone pozwalają wygodnie reprezentować wszystkie ruchy sztywne płaszczyzny, czyli przekształcenia zachowujące odległości między punktami oraz orientację płaszczyzny; z kursu geometrii wiemy, że są one złożeniami przesunięć i obrotów wokół punktu 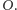 Analityczny opis takich przekształceń w klasycznej geometrii używa aż szóstki liczb; użycie liczb zespolonych pozwala na znacznie prostszy opis.
Analityczny opis takich przekształceń w klasycznej geometrii używa aż szóstki liczb; użycie liczb zespolonych pozwala na znacznie prostszy opis.
"Prawdziwa" geometria, tj. geometria, której używają mechanicy oraz astronomowie, rozgrywa się w przestrzeni trójwymiarowej  Wiadomo, że każdy ruch sztywny tej przestrzeni jest złożeniem pewnego przesunięcia oraz obrotu wokół jednej z osi przechodzących przez punkt
Wiadomo, że każdy ruch sztywny tej przestrzeni jest złożeniem pewnego przesunięcia oraz obrotu wokół jednej z osi przechodzących przez punkt 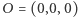 ; analityczny opis takiego przekształcenia potrzebuje aż 12 liczb. W tej sytuacji musiało pojawić się bardzo naturalne pytanie: czy trójwymiarową przestrzeń kartezjańską
; analityczny opis takiego przekształcenia potrzebuje aż 12 liczb. W tej sytuacji musiało pojawić się bardzo naturalne pytanie: czy trójwymiarową przestrzeń kartezjańską 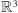 można wyposażyć w strukturę ciała tak, by dodawanie oraz mnożenie przez jego elementy prosto opisywało wszystkie ruchy sztywne tej przestrzeni?
można wyposażyć w strukturę ciała tak, by dodawanie oraz mnożenie przez jego elementy prosto opisywało wszystkie ruchy sztywne tej przestrzeni?

William R. Hamilton (1805-1865)
Irlandzki matematyk, fizyk i astronom William Rowan Hamilton strawił 10 lat na poszukiwaniu odpowiedniej struktury ciała na zbiorze trójek liczb rzeczywistych, analogicznej do struktury ciała liczb zespolonych na zbiorze par.
Z dodawaniem nie ma problemu: podobnie jak w przypadku dwuwymiarowym trójki liczb dodajemy po współrzędnych: 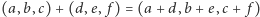 ; dodawanie ustalonego elementu
; dodawanie ustalonego elementu 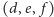 odpowiada wówczas przesunięciu przestrzeni o wektor
odpowiada wówczas przesunięciu przestrzeni o wektor ![[d,e, f ].](/math/temat/matematyka/algebra/2016/09/30/Liczby_zespolone_i_kwaterniony/3x-08e3e63463a6286b93d63189d22905738834d34a-im-33,33,33-FF,FF,FF.gif) Natomiast mnożenie trzeba wymyślić.
Natomiast mnożenie trzeba wymyślić.
Trójki liczb, czyli punkty w 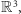 można też utożsamić z końcami wektorów, zaczepionych w punkcie
można też utożsamić z końcami wektorów, zaczepionych w punkcie 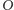 i szukać odpowiedniego mnożenia wektorów. Przywodzi to na myśl znane z zastosowań w mechanice i elektromagnetyzmie pojęcie iloczynu wektorowego
i szukać odpowiedniego mnożenia wektorów. Przywodzi to na myśl znane z zastosowań w mechanice i elektromagnetyzmie pojęcie iloczynu wektorowego 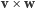 pary wektorów
pary wektorów 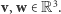 Wynikiem tego działania jest trzeci wektor, prostopadły do obu wektorów
Wynikiem tego działania jest trzeci wektor, prostopadły do obu wektorów 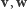 i skierowany w taką stronę, by trójkę wektorów
i skierowany w taką stronę, by trójkę wektorów 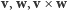 można było ruchem sztywnym przełożyć na dodatnie półosie
można było ruchem sztywnym przełożyć na dodatnie półosie 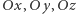 (niekoniecznie prostokątnego) układu współrzędnych. Ponadto, długość wektora
(niekoniecznie prostokątnego) układu współrzędnych. Ponadto, długość wektora  powinna być równa polu równoległoboku, rozpiętego przez wektory
powinna być równa polu równoległoboku, rozpiętego przez wektory 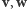 - łącznie warunki te wyznaczają wektor
- łącznie warunki te wyznaczają wektor 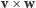 w sposób jednoznaczny. Niestety, to nie jest mnożenie, które może nas zadowolić. Z powyższej definicji wynika, że dla dowolnego wektora
w sposób jednoznaczny. Niestety, to nie jest mnożenie, które może nas zadowolić. Z powyższej definicji wynika, że dla dowolnego wektora  mamy
mamy 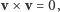 bo para
bo para 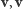 rozpina "równoległobok" o zerowym polu. Tymczasem w ciele iloczyn niezerowych elementów jest zawsze różny od zera; jeśli bowiem
rozpina "równoległobok" o zerowym polu. Tymczasem w ciele iloczyn niezerowych elementów jest zawsze różny od zera; jeśli bowiem 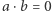 oraz
oraz 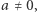 to istnieje
to istnieje 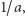 skąd dostajemy
skąd dostajemy

Wykażemy, że w przestrzeni 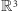 w ogóle nie ma takiego mnożenia, jakiego szukamy. Dowód poprowadzimy nie wprost. Załóżmy zatem, że istnieje szukane mnożenie, które sprawia, że
w ogóle nie ma takiego mnożenia, jakiego szukamy. Dowód poprowadzimy nie wprost. Załóżmy zatem, że istnieje szukane mnożenie, które sprawia, że 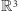 staje się ciałem. Wybierzmy dowolny element
staje się ciałem. Wybierzmy dowolny element 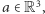 który nie należy do prostej zawierającej jedynkę tego ciała i niech
który nie należy do prostej zawierającej jedynkę tego ciała i niech 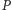 będzie płaszczyzną rozpiętą przez punkty
będzie płaszczyzną rozpiętą przez punkty 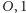 oraz
oraz 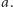 W szczególności, dowolny element
W szczególności, dowolny element 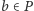 jest postaci
jest postaci 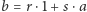 dla pewnych liczb
dla pewnych liczb 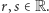 Rozważymy dwa przypadki:
Rozważymy dwa przypadki:
Przypadek I
Punkt 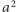 należy do płaszczyzny
należy do płaszczyzny 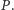 Wobec tego dla
Wobec tego dla 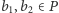 mamy
mamy

czyli płaszczyzna 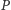 jest podzbiorem zamkniętym ze względu na mnożenie.
jest podzbiorem zamkniętym ze względu na mnożenie.
Ponadto, dla ustalonego 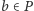 przekształcenie płaszczyzny
przekształcenie płaszczyzny 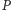 w siebie, dane wzorem
w siebie, dane wzorem 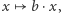 jest różnowartościowym przekształceniem liniowym: jeśli
jest różnowartościowym przekształceniem liniowym: jeśli 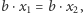 to
to 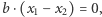 a skoro
a skoro 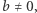 to
to 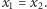 Wynika stąd, że obrazem
Wynika stąd, że obrazem 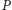 jest cała płaszczyzna
jest cała płaszczyzna 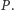 W szczególności, istnieje taki element
W szczególności, istnieje taki element 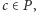 że
że 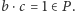 Wynika stąd, że
Wynika stąd, że 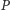 jest dwuwymiarowym podciałem w naszym ciele
jest dwuwymiarowym podciałem w naszym ciele 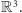
Wybierzmy teraz dowolny element 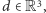 leżący poza płaszczyzną
leżący poza płaszczyzną 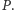 Wówczas podzbiór
Wówczas podzbiór 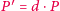 także jest płaszczyzną. Rozważmy przecięcie
także jest płaszczyzną. Rozważmy przecięcie 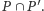 Załóżmy, że dla pewnych niezerowych
Załóżmy, że dla pewnych niezerowych 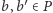 mamy
mamy 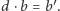 Wówczas
Wówczas 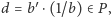 wbrew wyborowi
wbrew wyborowi 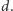 Wobec tego
Wobec tego 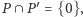 co daje sprzeczność, gdyż w przestrzeni trójwymiarowej dwie płaszczyzny nie mogą przecinać się w dokładnie jednym punkcie.
co daje sprzeczność, gdyż w przestrzeni trójwymiarowej dwie płaszczyzny nie mogą przecinać się w dokładnie jednym punkcie.
Przypadek II
Punkt 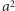 nie należy do płaszczyzny
nie należy do płaszczyzny 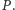 Wówczas wektory
Wówczas wektory 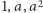 rozpinają przestrzeń
rozpinają przestrzeń 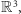 więc
więc 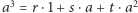 dla pewnych liczb
dla pewnych liczb 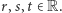 Wielomian
Wielomian 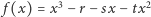 przyjmuje dla bardzo dużych
przyjmuje dla bardzo dużych 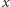 wartości dodatnie, zaś dla "bardzo ujemnych"
wartości dodatnie, zaś dla "bardzo ujemnych" 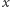 - wartości ujemne. Zatem ma on pierwiastek rzeczywisty
- wartości ujemne. Zatem ma on pierwiastek rzeczywisty 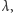 skąd
skąd 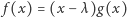 dla pewnego trójmianu
dla pewnego trójmianu 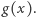 Podstawiając do tej tożsamości
Podstawiając do tej tożsamości 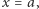 otrzymujemy
otrzymujemy

Ale 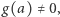 gdyż
gdyż 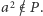 Zatem
Zatem 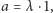 wbrew wyborowi
wbrew wyborowi 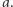
W obu przypadkach uzyskaliśmy sprzeczność, co dowodzi, że poszukiwana struktura ciała na przestrzeni 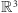 nie istnieje.
nie istnieje.
To, co nie jest możliwe w przestrzeni trójwymiarowej, może się zdarzyć w wymiarze 4. Na przykład, w przestrzeni 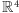 składającej się z czwórek liczb rzeczywistych jest dość miejsca na to, by dwie płaszczyzny miały dokładnie jeden punkt wspólny. Oto przykład: niech
składającej się z czwórek liczb rzeczywistych jest dość miejsca na to, by dwie płaszczyzny miały dokładnie jeden punkt wspólny. Oto przykład: niech 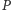 będzie płaszczyzną rozpiętą przez pierwsze dwie osie układu współrzędnych, zaś
będzie płaszczyzną rozpiętą przez pierwsze dwie osie układu współrzędnych, zaś 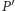 - przez ostatnie dwie. Do płaszczyzny
- przez ostatnie dwie. Do płaszczyzny 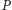 należą czwórki liczb postaci
należą czwórki liczb postaci 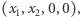 natomiast do
natomiast do 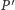 - czwórki
- czwórki 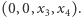 Jedyną czwórką, która jest obydwu tych postaci, jest, oczywiście,
Jedyną czwórką, która jest obydwu tych postaci, jest, oczywiście, 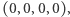 skąd
skąd 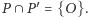
Hamilton dostrzegł możliwości przestrzeni czterowymiarowej w kontekście rozważanego problemu w dniu 16. października 1843 roku, gdy zmierzając w towarzystwie żony na posiedzenie Royal Irish Academy, przekraczał mostek Broom Bridge na Royal Canal w Dublinie.
Gdy wersory kolejnych osi 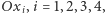 nazwiemy
nazwiemy 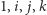 oraz zażądamy, by
oraz zażądamy, by

otrzymamy niemal idealne czterowymiarowe ciało!
Hamilton był tak podekscytowany swoim odkryciem, że ponoć wydrapał powyższe formuły na kamiennej poręczy mostu. Historia milczy, jak zareagowała na to zdarzenie towarzysząca mu małżonka.
Odczytajmy z powyższych wzorów wynik mnożenia każdej pary liter 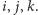 Mnożąc równość
Mnożąc równość 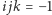 z prawej strony przez
z prawej strony przez 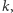 otrzymamy
otrzymamy

Wykonując podobne mnożenie przez 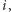 ale z lewej strony, otrzymamy
ale z lewej strony, otrzymamy 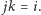 Z pierwszej z otrzymanych powyżej równości można wyliczyć
Z pierwszej z otrzymanych powyżej równości można wyliczyć 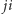 :
:

Wynika stąd, że 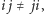 czyli nasze mnożenie nie jest przemienne, co tłumaczy użyte wyżej określenie niemal idealne.
czyli nasze mnożenie nie jest przemienne, co tłumaczy użyte wyżej określenie niemal idealne.
Pozostawiamy Czytelnikom fascynującą zabawę uzyskania kompletu równości:

Każda czwórka 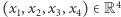 może być zapisana jako kwaternion
może być zapisana jako kwaternion 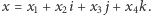 Takie wyrażenia dodajemy po współrzędnych - jak liczby zespolone. Natomiast mnożymy je, otwierając nawiasy i korzystając z sześciu równości przedstawionych wyżej. Tak powstaje algebra kwaternionów , którą na cześć Hamiltona oznaczamy symbolem
Takie wyrażenia dodajemy po współrzędnych - jak liczby zespolone. Natomiast mnożymy je, otwierając nawiasy i korzystając z sześciu równości przedstawionych wyżej. Tak powstaje algebra kwaternionów , którą na cześć Hamiltona oznaczamy symbolem 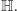
Czy każdy niezerowy kwaternion ma element odwrotny? Dla liczb zespolonych pomogło rozważenie iloczynu 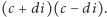 Tu postąpimy podobnie; gdy uważnie wykonamy mnożenie, otrzymamy
Tu postąpimy podobnie; gdy uważnie wykonamy mnożenie, otrzymamy

Gdy 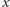 jest kwaternionem niezerowym, tj. gdy choć jedna z liczb
jest kwaternionem niezerowym, tj. gdy choć jedna z liczb 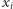 jest różna od zera, suma po prawej stronie jest niezerowa. Gdy wszystkie współczynniki drugiego czynnika w powyższym iloczynie podzielimy przez tę sumę, uzyskamy postać poszukiwanego elementu
jest różna od zera, suma po prawej stronie jest niezerowa. Gdy wszystkie współczynniki drugiego czynnika w powyższym iloczynie podzielimy przez tę sumę, uzyskamy postać poszukiwanego elementu 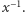 Zatem
Zatem 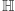 jest naprawdę ciałem, tyle że nieprzemiennym.
jest naprawdę ciałem, tyle że nieprzemiennym.
A co w takim razie z wyjściowym celem, jakim było wyrażenie obrotów przestrzeni trójwymiarowej za pomocą mnożenia w odpowiednim ciele? Otóż ten cel też udaje się zrealizować w następujący sposób. Umieśćmy naszą przestrzeń trójwymiarową wewnątrz 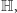 na ostatnich trzech osiach, tj. jako zbiór "czysto urojonych" kwaternionów
na ostatnich trzech osiach, tj. jako zbiór "czysto urojonych" kwaternionów 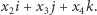 Niech
Niech 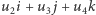 będzie wektorem długości 1, wskazującym oś obrotu, który chcemy zrealizować oraz niech
będzie wektorem długości 1, wskazującym oś obrotu, który chcemy zrealizować oraz niech 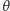 będzie kątem, o jaki chcemy obrócić przestrzeń. Rozważmy kwaternion
będzie kątem, o jaki chcemy obrócić przestrzeń. Rozważmy kwaternion

oraz przekształcenie 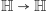 dane wzorem
dane wzorem 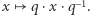 Łatwo zauważyć, że prosta rozpięta przez wektor
Łatwo zauważyć, że prosta rozpięta przez wektor 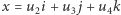 nie poruszy się. Okazuje się, że przekształcenie to przeprowadza czysto urojoną podprzestrzeń na siebie i wykonuje na niej dokładnie ten obrót, który sobie zaplanowaliśmy.
nie poruszy się. Okazuje się, że przekształcenie to przeprowadza czysto urojoną podprzestrzeń na siebie i wykonuje na niej dokładnie ten obrót, który sobie zaplanowaliśmy.
Wobec tego każdy obrót przestrzeni trójwymiarowej potrafimy zakodować za pomocą czwórki liczb rzeczywistych. Jest to na tyle efektywne, że kwaterniony znajdują zastosowanie w grafice komputerowej, do kodowania szybkich animacji.
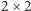 i wektor, a nawet może się upierać, że tych liczb mogłoby być mniej (trzy i pół), bo współczynniki macierzy nie są niezależne.
i wektor, a nawet może się upierać, że tych liczb mogłoby być mniej (trzy i pół), bo współczynniki macierzy nie są niezależne.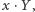 gdzie
gdzie 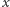 jest liczbą, a
jest liczbą, a 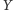 zbiorem liczb, rozumiemy zbiór wszystkich liczb, które można uzyskać jako iloczyn
zbiorem liczb, rozumiemy zbiór wszystkich liczb, które można uzyskać jako iloczyn 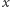 przez którąś z liczb ze zbioru
przez którąś z liczb ze zbioru