Równania algebraiczne

Równania algebraiczne, czyli takie, które można zapisać, przyrównując wielomian do zera, intrygowały ludzi od bardzo dawna. Rozwiązywaniem równań zajmowano się już w czasach starożytnych. W szkole uczą nas, jak rozwiązywać równania liniowe i kwadratowe, to jest takie, w których występuje funkcja liniowa (wielomian stopnia pierwszego) albo funkcja kwadratowa (wielomian stopnia drugiego). Matematycy włoscy podali w XVI wieku wzory na pierwiastki równań stopnia trzeciego i czwartego. A co z równaniami wyższych stopni?

Odpowiedź przyszła dopiero w interesujących nas czasach, tj. na początku XIX wieku. Prace Ruffiniego (1765-1822), Abela (1802-1829), Galois (1811-1832) wyjaśniły tę sprawę do końca.

Uznajemy, że rozwiązaliśmy równanie algebraiczne, jeżeli jego pierwiastki potrafimy wyrazić - podobnie jak w przypadku równania kwadratowego - przez współczynniki równania za pomocą czterech działań algebraicznych i operacji wyciągania pierwiastków (być może wysokiego stopnia). Jeśli pierwiastki równania potrafimy wyrazić w taki sposób, to mówimy, że równanie można rozwiązać przez pierwiastniki. Paolo Ruffini podał w roku 1799 dowód (niestety, nieścisły) twierdzenia mówiącego o tym, że ogólnego równania stopnia piątego nie można rozwiązać przez pierwiastniki. Wynika stąd, że nie można rozwiązać przez pierwiastniki ogólnego równania dowolnego stopnia 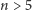$n > 5$ . Dokładny dowód twierdzenia o nierozwiązalności przez pierwiastniki równań stopni 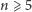$n ⩾5$ podał w roku 1824 Niels Henrik Abel. Twierdzenie to nie głosi, że żadnego równania stopnia piątego albo wyższego nie można rozwiązać. Oczywiście, potrafimy podać równania, które można rozwiązać, np. równanie stopnia piątego 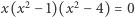$2 2 x(x − 1)(x − 4) = 0$ rozwiążemy bez trudu. Trochę więcej wysiłku włożymy w rozwiązywanie równania

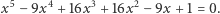x5 − 9x4 + 16x3 + 16x2 −9x + 1 = 0.

(1)

Najpierw zauważmy, że pierwiastkiem tego równania jest liczba 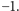$|−1.$ Wielomian 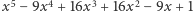$x5 − 9x4 + 16x3 +16x2 − 9x + 1$ dzielimy więc przez dwumian 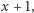$|x +1,$ otrzymując 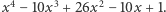$x4 −10x3 +26x2 − 10x +1.$ Obie strony równania 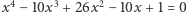$4 3 2 |x − 10x + 26x − 10x + 1 = 0$ dzielimy teraz przez 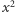$2 x$ otrzymując równoważne równanie

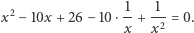1 1 x2 −10x + 26− 10 ⋅--+ -2 = 0. x x

(2)

Przyjmijmy teraz

-1 t = x + x ,

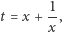(3)

więc

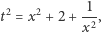
t2 = x2 + 2+ 1-, x2

zatem nasze równanie przyjmie postać 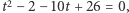$2 t − 2− 10t+ 26 = 0,$ a więc 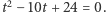$|t2 −10t +24 = 0.$ Pierwiastkami tego równania kwadratowego są liczby 4 i 6. Podstawiając te wartości do (3) dostajemy

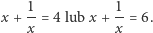
1- -1 x + x = 4 lub x + x = 6.

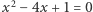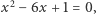Stąd mamy równania kwadratowe $x2 − 4x +1 = 0$ i $|x2− 6x + 1 = 0,$ których pierwiastkami są odpowiednio liczby 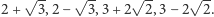$√ -- √ -- √ -- √ -- |2+ 3,2− 3,3 +2 2,3 − 2 2.$ Ostatecznie więc pierwiastkami równania (1) są właśnie te liczby i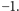 $|−1.$

Istnieją jednak takie równania, których nie można rozwiązać przez pierwiastniki, np. równanie 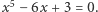$5 x −6x + 3 = 0.$

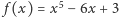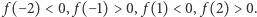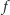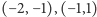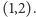Rozważmy funkcję $f (x) = x5 − 6x + 3$ określoną w zbiorze liczb rzeczywistych. Jest to funkcja ciągła i $| f(−2) < 0, f(−1) > 0, f (1) < 0, f(2) > 0.$ Wynika stąd, że funkcja $| f$ ma swoje miejsca zerowe w przedziałach $|(−2,−1),(−1,1)$ i $|(1,2).$ Można wykazać, że więcej miejsc zerowych nie ma. 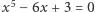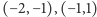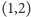Wobec tego równanie $|x5− 6x + 3 = 0$ ma trzy pierwiastki rzeczywiste leżące w przedziałach $|(− 2,−1),(−1,1)$ i $|(1,2)$ oraz dwa pierwiastki zespolone sprzężone. Żadna z tych pięciu liczb nie wyraża się przez pierwiastniki.

Odpowiedź na pytanie, kiedy pierwiastki danego równania wyrażają się przez pierwiastniki, zawarł w swoich pracach Evariste Galois. Jako kilkunastoletni młodzieniec wysłał te prace do Akademii Francuskiej, gdzie nie znalazły one zrozumienia. Dopiero wiele lat po tragicznej śmierci Galois (zginął w pojedynku) zrozumiano i doceniono jego osiągnięcia.

Aby odpowiedzieć na pytanie o rozwiązalność konkretnego równania, należałoby rozważyć najmniejsze ciało liczbowe, które zawiera wszystkie pierwiastki tego równania; tzw. ciało rozkładu wielomianu wyznaczającego to równanie. No, ale gdybyśmy znali te pierwiastki, to znaczyłoby, że potrafiliśmy je obliczyć, czyli rozwiązać równanie. Genialny pomysł Galois polega na tym, że zamiast rozważać to ciało rozkładu wielomianu, bada się grupę przekształceń tego ciała, zwanych automorfizmami. Zasadnicze twierdzenie teorii Galois orzeka, że dane równanie można rozwiązać przez pierwiastniki, jeśli grupa automorfizmów ma pewną własność - jest grupą rozwiązalną.